切比雪夫不等式及其应用

（北京交通大学附属中学 北京 100081）

一、基础理论知识

随机变量：

设X=X（ω）为定义在样本空间Ω上的实值函数，则称X 为随变量。若它仅取有限个或可列个值，则称其为离散型随机变量。若它的可能取值充满数轴上的一个区间（ a，b），则称其为连续性随机变量。[1]

分布函数：

二、切比雪夫不等式的应用

证明：由于{Xn}相互独立，从而有：

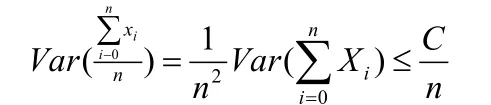
由切比雪夫不等式可得：

从而可得到：

结语

由上只是简单举例分析了切比雪夫不等式在证明常数方差为零，估值，依概率收敛上的应用，除了这些，切比雪夫不等式在证明马尔科夫不等式上也有相应的应用。这里不再赘述。