平均速度公式在高考中的巧用

（贵州省兴义五中 贵州兴义 562400）

在匀变速直线运动中求解物体通过的位移。大多数学生.包括很多老师都习惯用：

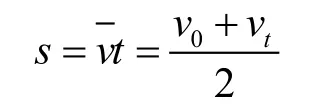
求解，在一些题目中的确很方便，但是如果能巧用平均速度公式：

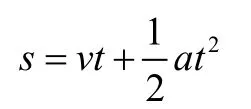
求解则会让求解更简单，特别是在往返直线运动中以及在处理时间问题上更能体现出其优点.在近几年的高考试题上如果能运用好平均速度公式试题就变得简单，更容易理解·下面就以2017年的两道高考试题为例说明如何使用平均速度位移公式来解题。体会公式的优越性。

一 （2017·全国Ⅱ卷，24）为提高冰球运动员的加速能力，教练员在冰面上与起跑线距离s0和s1（s1＜s0）处分别放置一个挡板和一面小旗，如图所示.训练时，让运动员和冰球都位于起跑线上，教练员将冰球以初速度v0击出，使冰球在冰面上沿垂直于起跑线的方向滑向挡板;冰球被击出的同时，运动员垂直于起跑线从静止出发滑向小旗.训练要求当冰球到达挡板时，运动员至少到达小旗处.假定运动员在滑行过程中做匀加速运动，冰球到达挡板时的速度为v1.重力加速度大小为g.求（1）冰球与冰面之间的动摩擦因数;

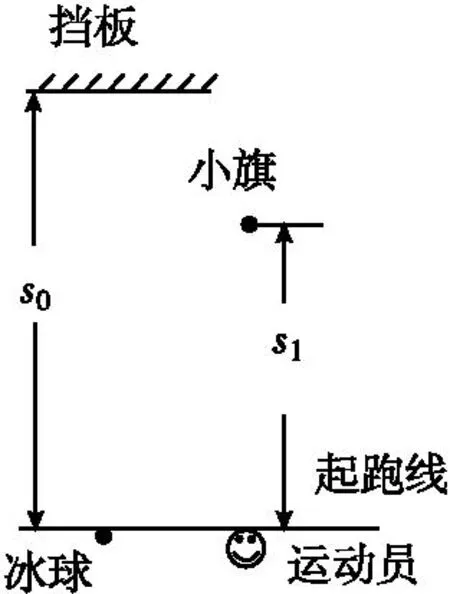
（2）满足训练要求的运动员的最小加速度.

解（1）略

（2）解法一（位移公式法）得冰球到达挡板时，满足训练要求的运动员中，刚好到达小旗处的运动员的加速度最小.设这种情况下，冰球和运动员的加速度大小分别为a1和a2，所用的时间为t.由运动学公式得

小结：在匀变速直线运动中涉及到位移和初，末速度，时间优先考虑使用平均速度公式求解这样会给解题带来了简便。避免了位移公式中时间上的平方计算。

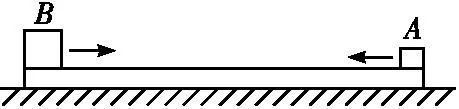
（2017·全国Ⅲ卷，25） 如图，两个滑块A和B的质量分别为mA=1 kg和mB=5 kg，放在静止于水平地面上的木板的两端，两者与木板间的动摩擦因数均为μ1=0.5;木板的质量为m=4 kg，与地面间的动摩擦因数为μ2=0.1.某时刻A，B两滑块开始相向滑动，初速度大小均为v0=3 m/s.A，B相遇时，A与木板恰好相对静止.设最大静摩擦力等于滑动摩擦力，取重力加速度大小g=10 m/s2.求

（1）B与木板相对静止时，木板的速度;

（2）A，B开始运动时，两者之间的距离.

解：（1）略

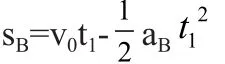
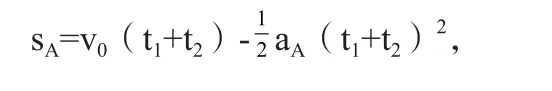
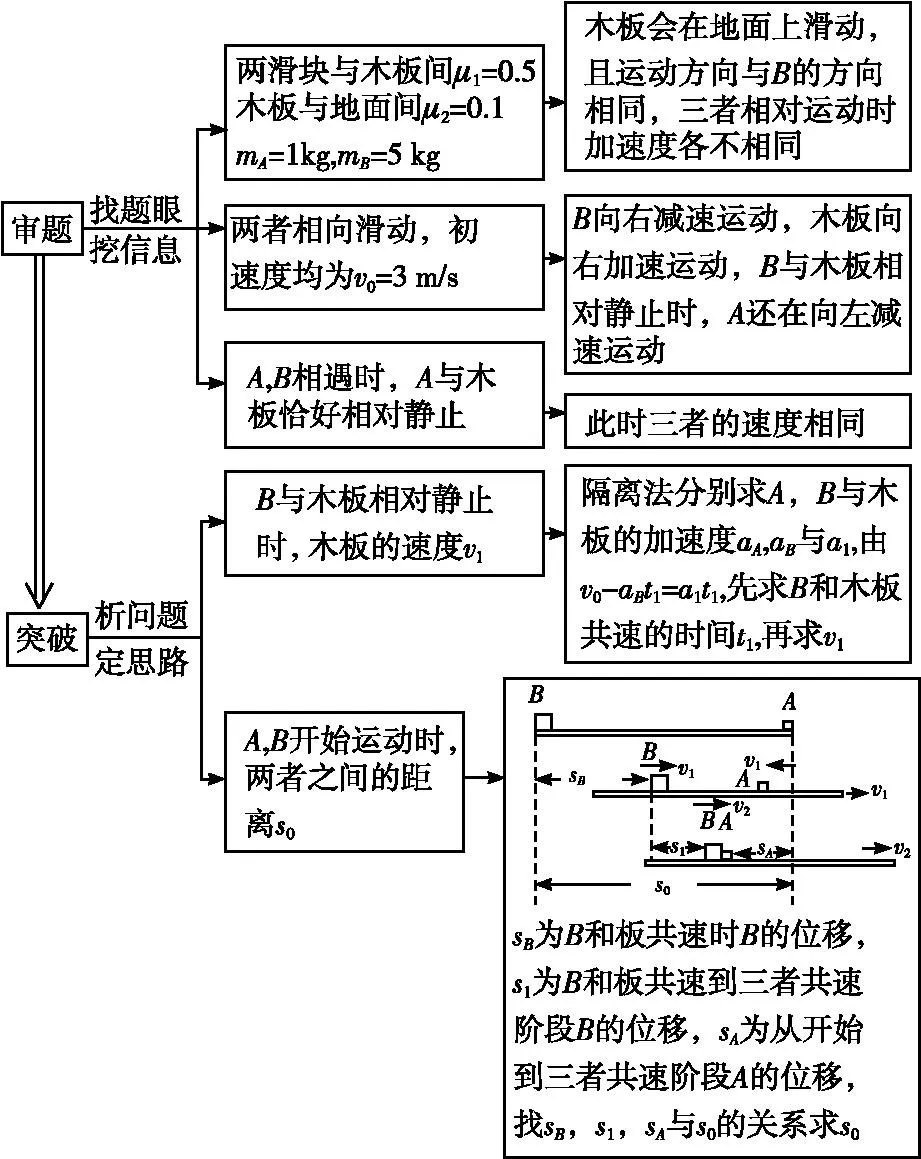
A和B相遇时，A与木板的速度也恰好相同.因此A和B开始运动时，两者之间的距离为s0=sA+s1+sB，联立以上各式，并代入数据得s0=1.9 m.

解法二（平均速度公式法）

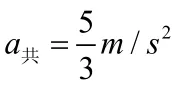
设B从开始到三者共速的时间为t总。共同速度为

v共2则有对A:vA=-v0+aAt. 对B:vB=v1-a共（t总-t1）

最后相遇有 v共2=VA=VB。 解得t总=0.7s.V共2=0.5m/s

所以两木板开始运动时二者的距离就是两者位移之和由平均速度公式.规定向右为正。

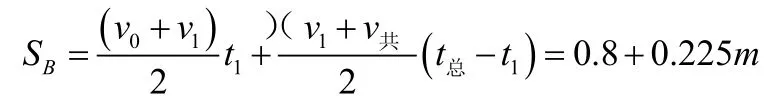
则有

结语

在匀变速直线运动这一类问题中.应该充分运用平均速度位移公式来解决与位移.时间.速度有关的问题。当已知位移和时间的关系时应该优先考虑平均速度位移公式。这样会给问题简单化。