利用滑动式切比雪夫多项式拟合卫星精密坐标和钟差

王 兴，高井祥，王 坚，李增科

(中国矿业大学国土环境与灾害监测国家测绘地理信息局重点实验室，江苏徐州221116)

一、引 言

在GPS数据处理中，需要精确的卫星坐标和钟差，可以利用精密星历给出卫星在空间的三维坐标及卫星钟改正数等信息获得，但是精密星历是按一定的时间间隔(15 min或5 min)给出的［1］。因此，需要使用合理的数学模型计算出任意时刻的卫星坐标。目前，利用精密星历求卫星坐标和钟差的方法主要有插值法和拟合法两类，但是在展开级数较高的情况下，拉格朗日插值法会产生振荡，而与之相比，切比雪夫拟合法则较为稳定。因此，在使用精密星历对卫星坐标和钟差进行插值过程中，一般多采用切比雪夫多项式拟合法［2］。

对于普通的切比雪夫拟合来说，大部分拟合时刻的点位误差都比较小，拟合精度高，但是也有小部分的误差较大。拟合时段的中间部分所得结果的精度相对来说比较一致，然而，在计算靠近拟合时段两个端点时刻时，卫星的坐标和钟差会出现数据跳跃的现象，使得端点时刻拟合的结果精度比较低［3］。为了解决这个问题，提高拟合的精度，本文提出了滑动式的切比雪夫算法。

二、切比雪夫多项式

切比雪夫多项式拟合即根据已知的数据拟合出一个多项式函数，使得这个函数在已知点的函数值与给定的函数值的方差和最小。根据精密星历给出的卫星坐标，可以拟合出卫星坐标随时间变化的函数，从而通过这个函数求出卫星在拟合范围内任意时刻的卫星位置。

由于切比雪夫多项式只适用于自变量区间为［－1，1］的情况，因此用n阶切比雪夫多项式来逼近时间段［t0，t0+Δt］中的卫星星历时，要先将变量 t∈［t0，t0+Δt］变换为变量 τ∈［－1，1］，即

于是卫星坐标(X，Y，Z)的切比雪夫多项式可表示为

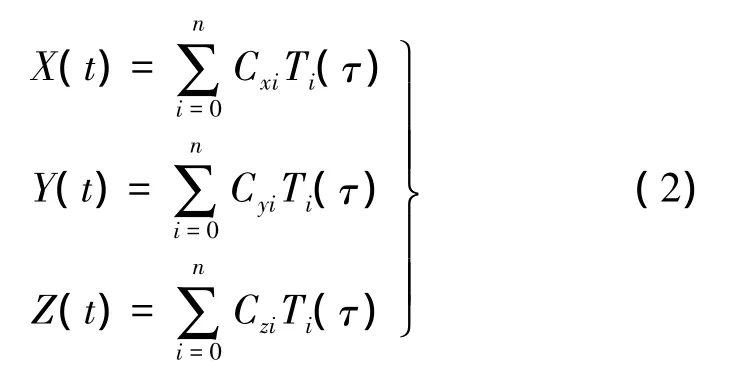
式中，n为多项式的阶数;Cxi、Cyi、Czi分别为 X 坐标分量、Y坐标分量、Z坐标分量的切比雪夫多项式系数。

根据已知的卫星坐标，用最小二乘法拟合出多项式系数 Cxi、Cyi、Czi，就可用式(2)计算出该时段中任一时刻的卫星位置［4］。切比雪夫多项式Ti的递推公式如下

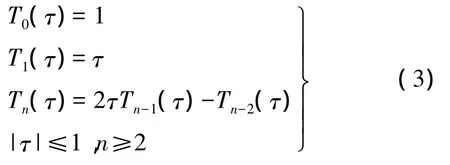
三、滑动式切比雪夫算法

所谓滑动式切比雪夫算法，就是不断地变换拟合区间，使要插值的点始终处于插值区间的中心。如第一次选取1～10这10个已知点，生成9阶的切比雪夫多项式进行拟合，但是只使用第5个已知点和第6个已知点之间的插值点的结果，其他点的结果舍弃不要;第二次选取2～11这10个已知点，生成9阶的切比雪夫多项式进行拟合，同样只使用第5个已知点和第6个已知点之间的插值点的结果。也就是相当于选定一个长度固定的区间，然后不断地让这个区间向右移动，每次拟合都只使用处于区间中心的插值点的结果。

如图1所示，矩形内的10个点即为已知数据点，而矩形可视为插值区间，阴影部分为使用的插值点结果，每次插值后，插值区间随之向右移动。

图1 滑动式切比雪夫算法示意图

由于在已知点中间部分的插值点的精度最好，这样就使得所有插值点的值都能获得较高的精度，更大大减少了端点数据点附近的插值跳跃现象［5］。因此，这种滑动式切比雪夫的算法与普通的切比雪夫算法相比，精度有所提高，数值较为稳定，不会出现误差较大的跳跃点，且通过简单的程序就可以实现，时间耗费不大，对于获得高精度的卫星坐标和钟差来说很有意义。

四、算例分析

本文采用的已知数据是由JAXA提供的2014年4月 3日间隔 5 min的精密星历，精密星历qzfg17864.sp3包含了 2014年 4月 3日 0:00至23:55共288个历元、29颗卫星的数据，选取PRN号为01的GPS卫星分别进行普通的切比雪夫拟合和滑动式切比雪夫拟合，并对比分析其结果。从各方面衡量，切比雪夫多项式的阶数选为9阶时，求得的GPS 卫星坐标效果较好［6］。

1.普通的切比雪夫拟合

选取以下10个时段分别进行切比雪夫拟合:1:00—3:15、3:15—5:30、5:30—7:45、7:45—10:00、10:00—12:15、12:15—14:30、14:30—16:45、16:45—19:00、19:00—21:15、21:15—23:30。

在每个时段内，选取15 min的倍数点作为已知点，如在第一个时段内，选取 1:00、1:15、1:30、…、3:15这10个点作为已知点，拟合出5 min间隔的插值点坐标和钟差，并与5 min间隔的精密星历提供的坐标和钟差作对比，得出误差结果。为便于与滑动式切比雪夫拟合作对比，截取1:00—22:45时间段内的坐标和钟差的插值结果。

2.滑动式切比雪夫拟合

选取 0:00、0:15、0:30、…、23:45 这些点作为数据点，精密星历给出了0:00—23:55的以5 min为间隔的卫星坐标和钟差，而滑动式切比雪夫拟合要保证每个拟合区间的前后都有5个数据点，如在拟合1:00—1:15时间段内的坐标和钟差时，向左选取0:00—1:00这5个数据点，向右选取1:15—2:15这5个数据点。因此，以5 min为间隔拟合出1:00—23:45时间段内的卫星坐标和钟差，其中，对于数据点处的坐标值和钟差不进行拟合，沿用精密星历给出的坐标值和钟差。将结果与精密星历提供的坐标和钟差作对比，得出误差结果。

3.结果分析

如图2—图4所示，普通的切比雪夫算法大部分的拟合误差都在－1～1 mm范围内，但是在拟合时段的端点处经常发生跳跃现象，误差突然变大，精度降低，稳定性比较差。

如图5—图7所示，滑动式切比雪夫拟合算法的所有坐标误差基本上都在－1～1 mm之间，拟合的结果较为稳定，无明显跳跃的值，相对于普通的切比雪夫拟合有了明显的改善。

如图8和图9所示，相比于卫星坐标的拟合来说，钟差的两种拟合方法在精度上的差别相对较小，但是，从图中可以明显看出，滑动式切比雪夫拟合所得到的钟差值稳定性较好。

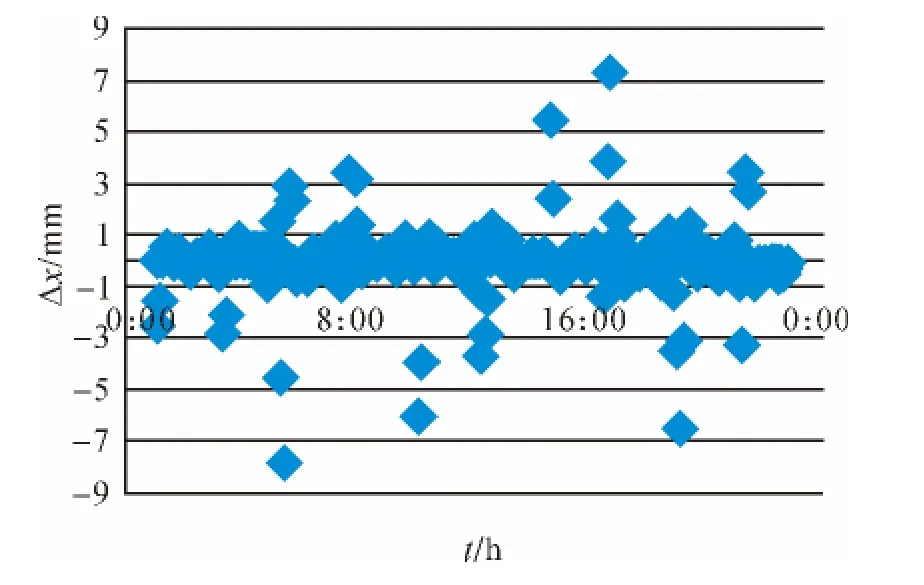
图2 普通的切比雪夫拟合得到的X坐标误差

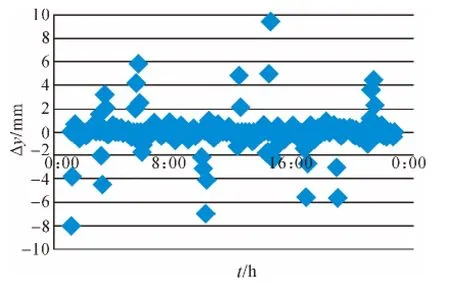
图3 普通的切比雪夫拟合得到的Y坐标误差

图4 普通的切比雪夫拟合得到的Z坐标误差

图5 滑动式切比雪夫拟合得到的X坐标误差

图6 滑动式切比雪夫拟合得到的Y坐标误差

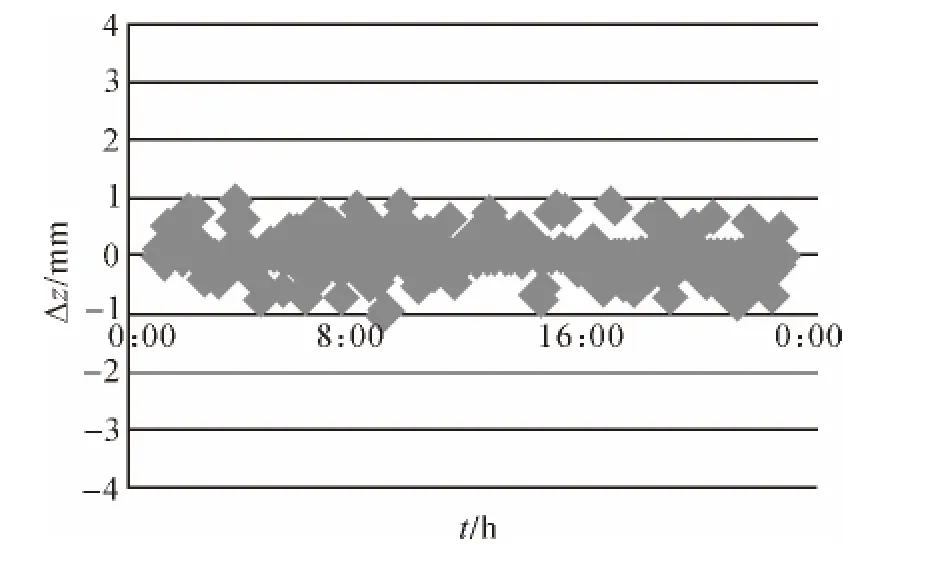
图7 滑动式切比雪夫拟合得到的Z坐标误差

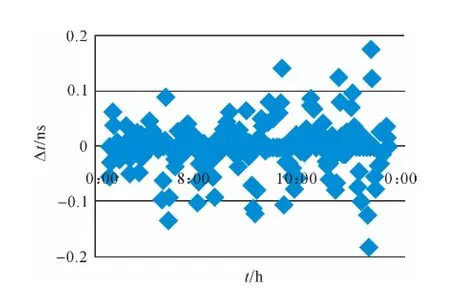
图8 普通的切比雪夫拟合得到的钟差误差

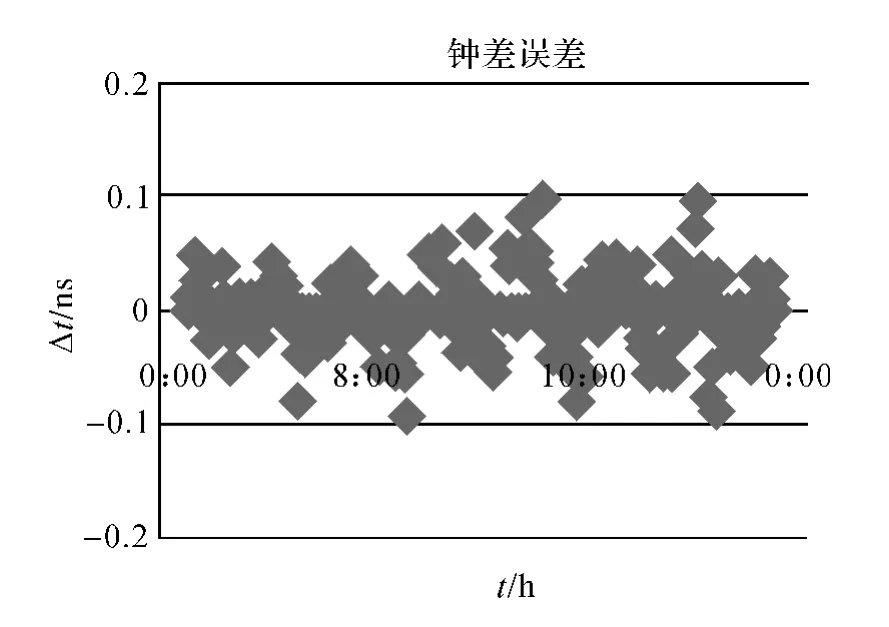
图9 滑动式切比雪夫拟合得到的钟差误差

由表1和表2可以看出，普通的切比雪夫拟合所得到的坐标及钟差的误差绝对值最大值要比滑动式切比雪夫拟合大很多。

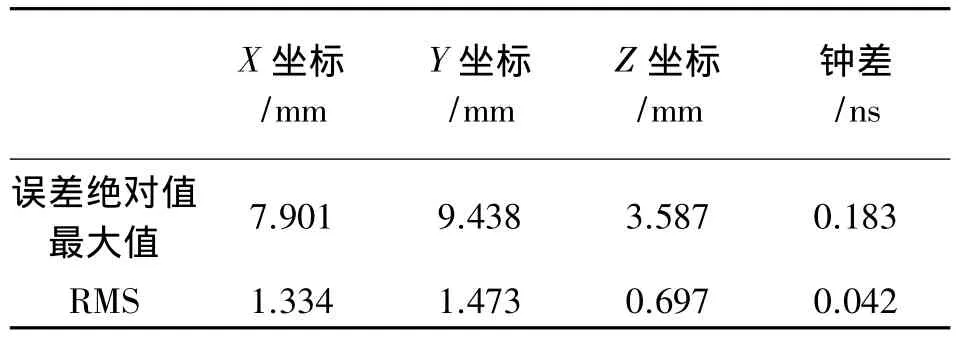
表1 普通的切比雪夫拟合得到的坐标和钟差精度

表2 滑动式切比雪夫拟合得到的坐标和钟差精度

五、结 论

1)总体上来说，滑动式切比雪夫拟合的误差稳定性要远远好于普通的切比雪夫拟合，不会出现明显的跳跃点，坐标的精度提高很多，钟差的精度提高相对较少。

2)从计算效率上看，滑动式切比雪夫拟合算法并不复杂，且与普通的切比雪夫拟合计算量相当，程序实现灵活方便。

3)文中滑动式切比雪夫拟合所得的为1:00—22:45之间的卫星坐标和钟差，若要获取全天的坐标和钟差，可使用当天及前一天、后一天的精密星历进行拟合，也可进行外推，不过精度会有所下降。

［1］李征航，黄劲松.GPS测量与数据处理［M］.武汉:武汉大学出版社，2005.

［2］杨学锋，程鹏飞，方爱平，等.利用切比雪夫多项式拟合卫星轨道坐标的研究［J］.测绘通报，2008(12):1-3.

［3］赖山东，王有亮，黄河清.利用精密星历计算卫星位置方法的比较［J］.江西测绘，2009(2):35-37，40.

［4］冯炜，薛志宏，邵佳妮，等.两种常用GPS星历拟合方法的精度分析［J］.大地测量与地球动力学，2010，30(1):145-149.

［5］洪樱，欧吉坤，彭碧波.GPS卫星精密星历和钟差三种内插方法的比较［J］.武汉大学学报:信息科学版，2006，31(6):516-518.

［6］李明峰，江国焰，张凯.IGS精密星历内插与拟合法精度的比较［J］.大地测量与地球动力学，2008，28(2):77-80.