通过空间相似度设置阈值的Douglas-Peucker算法
贾钰涵,冯建华,蔡昕楠,刘 斌
(1.长安大学地质工程与测绘学院,陕西 西安 710054; 2.西安航天天绘数据技术有限公司,陕西 西安 710065)
地图综合一直以来都是地图学领域的重点和难点之一。根据地图要素的分类,综合主要针对点状要素的取舍、线状要素的化简以及面状要素轮廓的化简与合并3个方面[1]。线状要素作为地图的重要组成部分,对于线状要素的化简方法是研究的热点[2-3]。
线状要素化简的基本思想是在维持其形状的同时减少节点的数量[4]。针对线状要素的化简,前人提出了很多方法,如Douglas-Peucker(DP)算法[5]、Li-Openshaw算法[6]、弯曲组算法[7]等,各种算法的化简效果各有差异,其中DP算法作为最经典的算法,在地图综合中得到了广泛应用,不断有学者对其进行研究[8-10],并且其在除了地图综合外的其他领域也有应用[11]。该算法实现简单,化简效率高,在对整个线状地物进行化简的同时,可以很好地保留其形状特征,并且不会产生多余的点[12]。
尽管如此,DP算法在进行化简时需要人为选取阈值。阈值的设置直接关系到化简结果,若阈值设置过大,那么化简结果会变得粗略,无法保持线状地物的特征;若阈值设置过小,那么化简结果会过于详细,化简结果也不太理想。通常,在使用该算法时,制图人员需要不断调整阈值,并对化简的中间结果进行比较才能够得到最为合适的化简结果[13]。
线状要素的化简过程本质上是一种相似变换,通过研究化简前后线状要素间的空间相似度和DP算法阈值的关系,便可以根据空间相似度来选取合适的阈值,避免不断重复以选取最优阈值的繁琐过程,提高了化简的效率,降低了化简的主观性。
1 Douglas-Peucker算法
Douglas-Peucker算法在1973年由D.Douglas和T.Peucker提出[5],算法的步骤如下:
(1) 首先将线的首尾端点AB连成一条直线,遍历线上其他所有的点,并算出这些点距离这条直线的距离,找到最大距离的点C,最大距离记为dmax。
(2) 比较该最大距离(dmax)与给定的化简阈值Dmax之间的关系,若最大距离小于阈值(dmax (3) 若最大距离大于等于阈值(dmax≥Dmax),那么保留最大距离(dmax)对应的点C,并且以该点为界,把线分为AC和CB两部分,并且对每部分继续重复使用上述方法,直到线上的所有点到对应直线的距离都小于给定的阈值。 空间相似性是人类认知地图中的重要概念,在手工制图阶段,地图综合质量是质检人员通过经验来比对原图和综合结果图之间的相似程度来确定的[14]。 空间相似度是[0,1]区间内的一个值,其基于空间相似关系计算得到,用于度量空间目标之间的相似程度,如果用百分比表示,则是0~100%之间的一个值。该值越大,空间目标间的空间相似度越高,当值为1时代表完全相似[15]。 空间相似度不仅可以评判化简前后空间目标之间的一致性,也可以作为评价制图质量好坏的依据。 吴立新等[16]认为空间相似关系包括了两方面的含义:空间目标几何形态上的相似以及空间目标(群组)结构上的相似。 形状是空间感知以及传递信息的重要因素,也被认为是描述线的最关键因素。通过对象的形状来计算空间相似度,可以有效解决自动综合的问题。对于单个线状地物的研究,并不需要考虑线状地物群之间结构的相似。因此,用线的形状来描述线的相似程度。 两幅地图之间的相似程度可以使用“相同程度”来描述评估。“相同程度”使用两幅地图之间一致或不一致的面积来表示地图间的相似程度[17]。线状地物在图上一般作为半依比例尺符号,由此,在不考虑线状地物的宽度时,长度就成为了最重要的因素,因此在研究中使用线状地物之间的公共长度来计算其化简前后的空间相似度。将化简前后的线状地物相应的端点叠加,就可以得出两者之间的公共长度,基于公共长度也就可以计算出两者之间的空间相似度。 基于公共长度计算相似度最简单的方法是:求得化简前后的线状地物之间的公共长度(两条直线重合的长度),线状地物间的相似度公共长度和化简前的线状地物的比值计算公式为 (1) 其中:a代表化简前的线段;b代表化简后的线段;l代表两条线段的公共长度;L代表化简前线段a的长度。相似度Sim由以上几个参数计算得出。 利用式(1)计算相似度有着很明显的缺陷:计算时并没有考虑到化简前后线状地物之间的邻近关系,只有完全重合的部分被认为是相似部分(如图1所示)。这种情况(实线为化简前,虚线为化简后)计算出来的两条线之间的相似度就会是0,很明显这是不符合人类的认知规律的。 图1 化简前后的线状地物Fig.1 Linear objects before and after simplification 在考虑化简前后线状地物之间的邻近关系后,基于公式(1)对计算相似的方法进行改进。在地图上,线状地物是由一系列的坐标点组成的,利用Douglas-Peucker算法进行化简时保留的是原始线状地物的首尾端点以及各分线段的端点。因此,在计算相似度时,给化简后的线状地物的各分线段赋予一个权重,该权重基于各分线段与化简前的线状地物对应的线段之间的距离,计算公式为 (2) 其中:n代表化简后的线状地物的线段数目;L代表化简前线状地物的长度;li代表化简后的第i段线段的长度;ωi代表该线段基于距离计算出的权重,计算方法为 (3) 其中:di代表化简前后线状地物对应线段之间的距离;li代表化简后该线段的长度。 di的计算方法如图2所示,其中:ABCD(虚线)为化简前的线段;AD(实线)为化简后的线段。计算B、C(除了重合的首尾端点)与化简后的线段AD之间的距离并求出平均数即为di。 图2 化简前后对应的线段Fig.2 Corresponding line segment before and after simplificatio 研究两者间关系的总体思路是首先通过DP算法,选取不同的阈值对线状地物进行化简,然后通过公式计算化简前后的线状地物间的空间相似度,最后通过曲线拟合的方式得到阈值和空间相似度间的关系。 DP算法的阈值是一个绝对的值(长度),对于不同的线状地物,选取相同的阈值进行化简后,得到的结果与原本的线状地物间的空间相似度一般不同。因此,将DP算法化简时选取的阈值转换为一种相对的阈值。 根据DP算法的特点,首先,将DP算法的化简阈值设为0,由此计算出化简时线状地物每一段的最大距离dmax,将最大距离去掉0值之后,形成一个从小到大的序列;然后,将最大距离点绘制在坐标轴上,依次连接成一条折线,并且计算该折线与坐标轴围成的面积Stotal(见图3);最后,计算折线上起点到所设置阈值点与坐标轴围成的面积Spart(见图4),那么该绝对阈值对应的相对阈值为两者面积之比(总面积为分母),即Spart/Stotal。 图3 Stotal的计算Fig.3 The calculation of Stotal 图4 Spart的计算Fig.4 The calculation of Spart 实验对象为一条线状地物,原始形状如图5所示。 图5 实验选取的线状地物Fig.5 Linear objects selected in the experiment 将所选取的线状地物计算出来的dmax中的0值去掉之后,分布情况见表1。 表1 最大距离在各个区间的数量 由表1可以看出,最大距离大部分处于0~1这个区间内,这也符合图上线状地物弯曲度不大,较为平缓的特点。因此,选取较多0~1的阈值进行实验,以此来观察阈值和相似度之间的关系。 首先使用DP算法设置不同的阈值对该线状地物进行化简,得到化简后的结果,部分结果如图6所示。 图6 部分化简结果Fig.6 Part of the simplication results 从化简结果中可以看出,随着阈值的增大,线状地物的形状化简的程度也在增大,当阈值大于3之后,线的形状已经变得十分简单,这也符合最大距离的分布范围。 通过相似度计算方法和阈值转换方法,计算出不同阈值下化简后的线状地物和原本线状地物之间的相似度,部分结果见表2。 通过线性拟合得出两者之间的关系。拟合优度是指拟合结果对观测值的拟合程度。度量拟合优度的统计量是可决系数(亦称确定系数)R2,R2最大值为1。R2的值越接近1,说明回归直线对观测值的拟合程度越好;R2的值越小,说明回归直线对观测值的拟合程度越差。 根据表2中数据,将相对阈值作为自变量,相似度作为因变量,得到的拟合结果如图7所示。 图7 拟合曲线Fig.7 Fitting results curve 表2 化简阈值和空间相似度 构造出的3种曲线的拟合优度R2分别为0.883、0.823 8、0.956 9,可以看出多项式拟合的拟合程度是最好的。 因此,选取多项式拟合的曲线作为计算相似度的结果,计算公式为 (4) 其中:t代表相对阈值,可由绝对阈值计算得来。 通过公式(4)即可建立阈值与空间相似度之间的关系,通过空间相似度可以更快获取到想要的化简结果,避免了频繁地选取阈值和比较。 DP算法是进行线化简时的一种非常经典的算法,但是在进行化简时需要进行多次实验才能确定合适的阈值。通过对DP算法的阈值和化简前后线之间的空间相似度之间的关系进行了研究,将原本的绝对阈值转换为相对阈值,选取线状地物进行实验,建立起DP算法的化简阈值和化简前后线状地物间空间相似度的关系。基于此,通过空间相似度即在利用DP算法进行化简时,避免了以往需要多次实验和比较才能选取到合适阈值的情况,提高了算法的效率。 但是,研究只针对一个线状地物做了实验得出结果,可能只是对某一类线状地物效果较好,若想得到适用于更多类型的线状地物的结果,仍需选取更多的数据进行实验。此外,在进行空间相似度的计算时,只考虑了公共长度这个因素,并没有考虑到空间相似度的其他影响因子,计算方法仍待改进。若能在后续研究中解决以上问题,所得结果也可用于自动制图综合。2 空间相似度
2.1 计算依据
2.2 计算公式

2.3 计算公式改进

3 空间相似度与DP算法阈值间的关系
3.1 阈值的转换
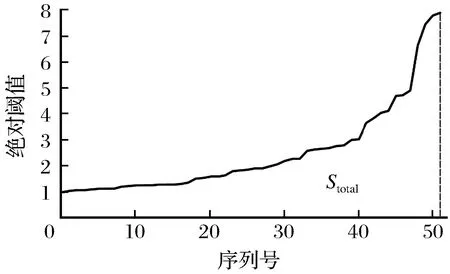

3.2 实验数据

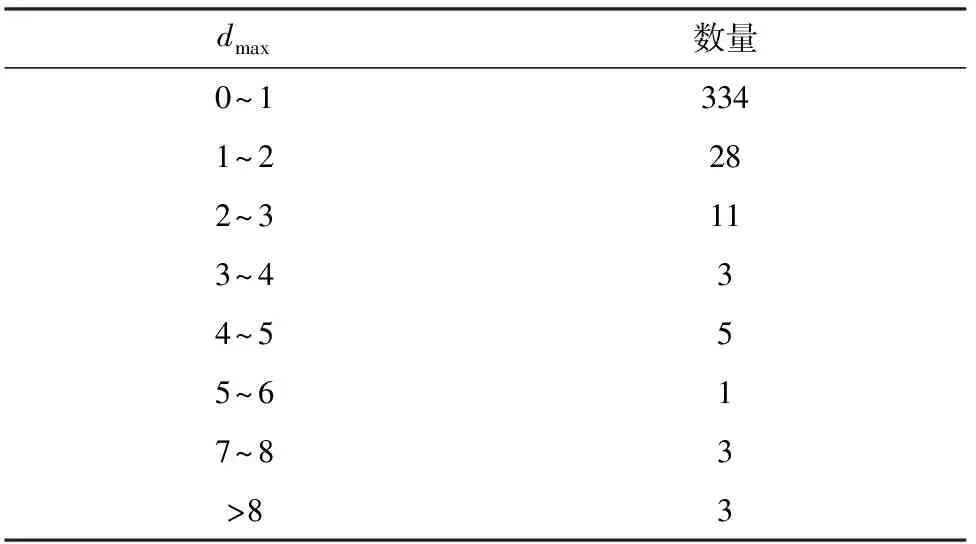
3.3 计算空间相似度

3.4 曲线拟合


4 结语

