信息技术对数学教学的三大促进
叶旭山 康叶红

摘要:当下是信息技术时代,各科教师都应积极促进信息技术与学科教学的融合,充分利用信息技术助力学科教学。结合信息技术的功能以及数学的特点﹑教学的要素,发现在数学教学中,信息技术能促进学习活动可视化、教学评价数据化、内容理解深度化。这三大促进作用能使数学教学具备三大显著特征:更生动直观、更精细准确、更深刻透彻。
关键词:信息技术;数学教学;学习活动;教学评价;内容理解
如今,信息技术对教育的影响日益深入,为教育提供了更多、更优的支持。《义务教育数学课程标准(2022年版)》在“课程理念”和“教学建议”中分别指出:促进信息技术与数学课程的融合②;注重信息技术与数学教学的融合③。也就是要利用信息技术助力数学教学。那么,如何做到这一点呢?
结合信息技术的功能以及数学的特点、教学的要素,我们认识到,在数学教学中,信息技术能促进学习活动可视化、教学评价数据化、内容理解深度化。这三大促进作用能使数学教学具备三大显著特征:更生动直观、更精细准确、更深刻透彻。
一、促进学习活动可视化
学习活动可视化主要是应用丰富多样的视觉表征手段,如图形、照片、动画、视频等,通过多媒体交互,将学生的学习过程和学习结果,以形象直观的方式近距离展现在全体学生面前,打破时空界限,激活思维,引发交流,帮助学生更好地发现数学、理解数学,让数学教学更加生动直观。
(一)学习过程可视化
数学教学中,通过数学软件、投屏工具等,可以将学生学习知识(解决问题)的演示过程直观呈現,降低学生思考的难度,暴露学生思维的过程。
例如,教学《最短路径》一课时,教师出示问题:
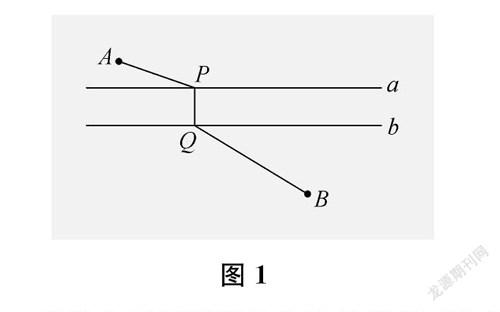
如图1,已知河岸a、b互相平行,村庄A、B在河的两侧。要造一座与河岸垂直的桥PQ,在哪里造才能使村庄A经过桥PQ到村庄B的路线最短?画出此时桥PQ的位置。
一名学生利用折纸的方法确定桥PQ的位置,具体过程如下:折叠画有图1的纸片,使直线a、b重合,连接AB,交直线a(b)于点P(Q);再展开折纸,连接PQ,即得桥PQ的位置。
教师利用iPad和“希沃白板”直播,把学生折纸解决问题的过程动态展现在全体学生面前,将抽象的数学过程直观、形象地展现出来,充分降低思考难度,暴露思维过程,让学生感受到折纸带来的思路创新。
试想,如果这一过程是由学生或教师口述完成的,其他学生可能就不能透彻理解这种解题方法。
(二)学习结果可视化
数学学习离不开解题(知识学习常常通过问题解决完成),解题结果是重要的学习结果。不同的学生在解题过程中,思维常常是多线迸发的,有一题多解的情况。借助信息技术,可以便捷地将有价值的解题结果直接展现,引发学生对思路、方法的分析比较,帮助学生理解思路、方法之间的共性与差异。
例如,一节习题课,教师出示例题:
如图2,在ΔABC中,点D、E是BC边上的两点,AD=AE,/BAD=/CAE。求证: AB=AC。
学生解答时,教师巡视,了解学生审题、解题的过程,及时捕捉现场生成的解答,然后利用iPad拍摄学生的正确解答和典型错误,借助“希沃白板”展示给全体学生(展示时的一个截屏如下页图3所示),从而引导学生分析比较,帮助学生进一步了解解题的规范要求和等腰三角形证明的相关思路。
二、促进教学评价数据化
教学是一项实践活动,需要基于对已有实践的评价,不断作出改进与完善。要让教学评价更客观准确、更充分精细,离不开对量化数据的收集、整理与分析。教学评价可以分为过程维度和结果维度,分别评价教学行为与教学效果。在相应的评价过程中,都可以充分发挥信息技术的作用。
(一)教学行为数据化
教学行为的评价,可以通过课堂观察的方式,直接或间接从课堂情境中收集、整理数据,并依据数据作出判断。课堂观察需要基于一定的观察量表,从具体的角度展开。当然,量表中的角度越多越细,得到的结果就越客观充分,但是观察的工作量也会越大,也就特别需要借助信息技术减轻负担,提高效率。
在实践中,我们借助“智能课堂助手”App观察课堂教学行为,基于特定的观察量表,收集、整理一系列数据进行分析。例如,课题组开展“平行四边形的性质”教学研讨时,借助“智能课堂助手”App,从多个角度表进行课堂观察,得到如图4所示的一系列数据,分析发现:在探究活动“平行四边形有什么性质?”中,学生专注度较高;整节课的用时分配合理,学生思考练习时间占整节课的64%,学生讨论/合作占27%,体现了学生是学习的主体;整节课总共提问72次,其中过渡型提问60次,记忆型提问1次,理解型提问12次,均在正常范围内。
(二)教学效果数据化
教学效果的评价,主要指学习情况的分析,可以通过纸笔测试的方式,根据学生答题情况收集、整理数据,并依据数据作出判断。为此,需要基于教学内容和目标(做好双向细目表)设计相应的测试题并赋予一定的分值。具体可以分为课时测试和阶段测试、教学前测和教学后测。课时测试反映课时学习情况,阶段测试反映阶段学习情况。教学前测可以了解学习基础,指导教学设计;基于教学前测,教学后测可以更好地检验教学效果,进一步指导教学改善。无论哪种测试,都可以借助信息技术处理各种数据,从而分析各题的得分情况,了解各位学生的知识掌握等学习情况(特别是薄弱之处);并且追踪多次测试的数据,了解各位学生学习情况的变化。
例如,一次区级期末考试后,教师借助数据处理软件,对学生的成绩做交互式统计分析,从难度、信度、效度等角度分析试卷,从平均分、最高分、最低分、学业等级、成绩分段等角度分析学情,从知识点(及能力点)、作答情况等角度分析试题,可视化呈现、多角度对比(部分数据如图5—图8所示),形成错题分析及个性化错题库等;进而追踪多次考试数据,依据知识图谱关系,有针对性地推送补偿练习,让不同的学生都能得到有效的发展。
三、促进内容理解深度化
数学作为一门高度抽象的学科,使得学生在学习中遇到了一定的困难:难以想象、体验数学现象发生和发展的过程。借助信息技术(主要是数学软件等工具)开展数学实验(促进数学体验),将数学中的抽象内容、动态内容等直观、具体地呈现给学生,可以帮助学生理解数学现象发生和发展的过程,降低理解难度,促进理解深度,让数学教学更加深刻透彻。
例如,《丰富的图形世界》一课,理解立体图形之间的变化关系是教学难点,对学生的空间想象能力和语言表达能力有较高的要求。对此,教师利用GeoGebra软件帮助学生理解。具体教学过程如下:
教师提问:“类比圆柱和圆锥之间的联系,棱柱和棱锥之间有联系吗?不妨以五棱柱和五棱锥为例,说说棱柱和棱锥之间有什么联系。”在教师的指导下,学生操作GeoGebra软件,感受“五棱柱→五棱锥”的变化过程(如图9所示),并交流形成结论。
教师依次追问:“仔细观察五棱柱变成五棱锥的过程,中途好像出现了一个新的几何体,这个几何体是什么呢?”“既然棱柱和棱錐之间存在棱台,那么,圆柱和圆锥之间有没有新几何体?”“棱柱和圆柱之间、棱锥和圆锥之间、棱台和圆台之间有联系吗?”在教师的指导下,学生操作GeoGebra软件,感受“柱→台→锥”和“棱→圆”的变化过程,并交流形成结论。教师进一步利用GeoGebra软件制作动态视频,让学生观察“点→线→面→三棱柱→50棱柱(近似圆柱)→圆柱→圆台→50棱台(近似圆台)→三棱台→三棱锥→50棱锥(近似圆锥)→圆锥→线一点”的变化过程(如图10所示)①,从而充分感受丰富的图形世界,深刻理解图形之间的关系,学会用动态的眼光观察图形。
再如,《二次函数的图像与性质》一课,苏教版初中数学教材直接从y=x的图像与性质开始,从特殊到一般,逐步研究y=ax、y=ax+n、y=a(x+m)2、y=a(x+m)2+n 的图像与性质,再基于y=ax2+bx+c与y=a(x+m)2+n的关系,研究y=ax2+bx+c 的图像与性质。对此,教师强化整体设计,引导学生基于对y=ax2+bx+c与y=a(x+ m)2+n关系的认识,针对y=a(x+m)2+n图像与性质的研究目标,设计完整的研究路径。在此基础上,教师利用GeoGebra软件增强直观效果,帮助学生理解参数a、m、n对y=a(x+m)2+n图像的影响(即认识不同函数图像之间的联系),明确研究路径,进而高效获得研究结论。大致教学过程如下:
教师提问:对于形如y=a(x+m)2+n的二次函数,如何一步步研究其图像与性质呢?
师生讨论,逐渐形成以下三条主要路径:(1)y=x→y=(x+m)2→y=(x+m)2+n→y =a(x+m)2+n;(2)y=x→y=x+n→y=(x +m)2+n→y=a(x+m)2+n;(3)y=x→y= a.x2→y=ax2+n→y=a(x+m)2+n。
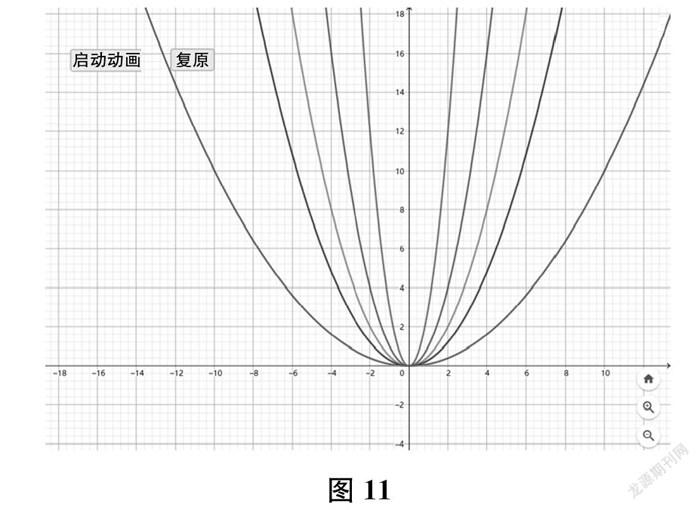
在教师的指导下,学生操作GeoGebra软件画出图像,并更改参数的数值(或通过图像的变化),感受参数a、m、n对y=a(x+m)2+n图像的影响(如图11—图14所示,其中图14为3个参数同时变化的情况),从而总结二次函数的图像与性质特征。
四、结语
当下是信息技术时代,各科教师都应积极促进信息技术与学科教学的融合,充分利用信息技术助力学科教学,发展学生的学科素养,培养学生的信息素养。最后要指出的是,在发挥信息技术对数学教学的三大促进作用的同时,教师还要把握信息技术与学科教学融合的两个基本原则:
一是辅助性原则。信息技术是辅助学科教学的。也就是说,信息技术是手段,学科教学是目的。教师不能为了技术而技术,而要从教学的需要出发使用技术,真正发挥技术的作用,使得技术的使用是有效的。
二是适用性原则。作为教学手段,不同的信息技术有不同的功能特点,适用于不同的教学目标(教学内容和对象)。教师要合理运用信息技术,包括多媒体、数学软件、网络平台等技术及有关资源,实现不同的教学目标。

