基于电压时间换相面积预测的换相失败抑制方法

朱仁龙，周小平，罗 安，洪乐荣，夏海涛，邓凌峰

（国家电能变换与控制工程技术研究中心（湖南大学），湖南省长沙市 410082）

0 引言

中国一次能源与电力需求的逆向分布促使输送距离远、容量大的高压直流输电技术得到了快速发展与广泛应用［1-2］。电网换相换流器型高压直流输电采用的晶闸管元件无自关断能力，在受端电网故障时有较大可能发生换相失败，这会致使直流电流迅速增大、直流电压迅速下降、传输功率迅速减小，故障严重时可能导致直流系统闭锁，对直流输电系统的高效、安全、稳定运行造成严重影响［3-4］。

文献［5-6］对直流输电系统换相失败的影响因素进行了较为全面的分析与总结，前者指出换流母线电压下降、越前触发角减小、直流电流增大、过零点偏移等因素易导致换相失败，后者从单一直流、多回路直流以及复杂系统3 个方面对换相失败的影响因素进行了分析，指出换相失败预测判据及控制措施应考虑多种因素。从控制上抑制换相失败的思路主要有降低直流电流指令和提前触发两大类。针对降低直流电流指令的方法，工程上广泛应用低压限流控制器（voltage dependent current order limiter，VDCOL）来降低换相失败的概率，文献［7-9］针对VDCOL 策略进行了改进使其更加灵敏。此外，文献［10］提出了直流电流预测控制与换相失败预防（commutation failure prevention，CFPREV）相结合的方法，但其电流指令参数较难整定。此外，降低电流指令的方法受到延时的制约，在抑制首次换相失败上具有一定局限性。针对提前触发的方法，根据触发角的求解方式可分为不具有和具有物理意义两类。前一类方法的最大特点就是部分参数需要整定，文献［11］通过宽频带电磁暂态电压在线监测装置测量所求得的电压暂态扰动量来对触发角进行调节，其触发角的提前量根据交流电压变化的幅值而定，且提前触发角控制策略的启动阈值和限幅上限都需要根据不同工程进行仿真来确定最优量。国外工程中所采用的CFPREV 及改进后的CFPREV 也是属于这类方法［12-13］。而后者具有物理意义方法的特点就是没有线性控制环节，通常也不需要进行参数整定。文献［14］对CFPREV 的触发角计算进行了优化，使其具有一定物理意义。文献［15］提出了一种改进预测型定关断角控制，其触发角预测值的表达式具有较为清晰的物理意义，但是该方法对换相过程进行了保守处理，在轻微扰动或者故障下会使得逆变站消耗无功更大，此外，触发角提前量过大还可能使得本来能够抑制换相失败却发生了换相失败。文献［16］在文献［15］的基础上通过泰勒公式的二阶展开更加精准地计及了换相过程直流电流的变化量，但同样对换相过程进行了保守处理。文献［17］利用三点法对故障前后电压波形进行拟合来求出所给触发角表达式中的电气量，但未考虑故障后换相过程中直流电流的变化。文献［18］通过简单测量实现换相面积的估算，但是其估算误差难以忽视，且该方法触发角指令更新时间还可提前。

对于提前触发这类方法的关键点是需要准确获得提前触发量，既要保证提前触发量能够使得下个阀臂成功换相，还要保证其触发量不至于过大使得逆变站无功需求增大、直流电流增大不利于换相过程。为此，本文通过测量换相开始与换相结束时刻，计算出当前换相过程的实际换相面积，间接避免了对故障后等效换相电抗变化的求解；同时，通过预测直流电流来预测下一换相过程需要的换相面积，在当前换相过程结束时刻，结合换相面积理论求解出下一换相过程的触发角预测值以实现抑制换相失败。基于国际大电网会议组织（CIGRE）标准模型对本文所提方法进行仿真验证，结果表明本方法可以在一定程度上抑制换相失败的发生。

1 换相失败发生机理分析

以晶闸管VT6向VT2换相为例，此时其逆变器等效电路如图1 所示。

图1 逆变器换相过程等效电路图Fig.1 Equivalent circuit of inverter during commutation

对换相回路由基尔霍夫电压定律列出式（1）。

式中：ub和uc分别为交流侧B、C 相电压；Lc为换相等效电感；i2和i6分别为通过VT2和VT6的电流。

式（1）移项变换后变为：

定义式（3）等号右边为需求换相面积［9］，有

式中：Aneed为需求换相面积，其值与等效换相电感、直流电流和换相角有关。

式（3）等号左边为实际换相面积：

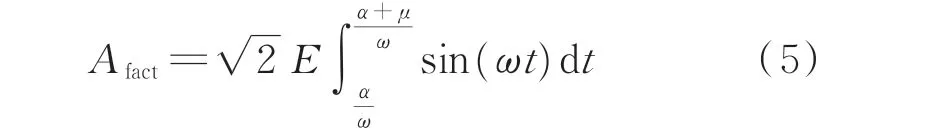
式中：Afact为实际换相面积，其值与换相电压有效值、触发角和换相角有关。

此时关断面积Aγ为：

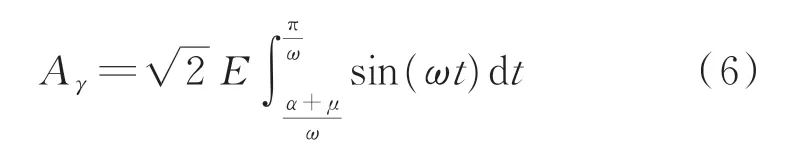
为了保证换相成功，在最小关断角γmin下有最小关断面积为：

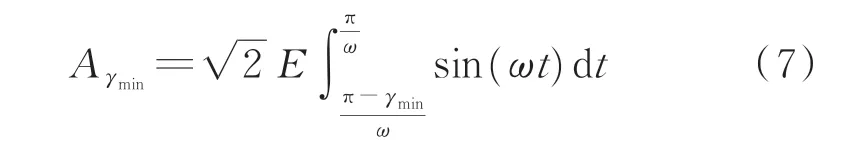
发生故障后，对于需求换相面积而言，直流电流增大导致需求换相面积增大。对于实际换相面积而言，换相电压下降导致实际换相面积减小。为了使得实际换相面积仍然等于需求换相面积以成功换相，换相角会被迫增大以增大实际换相面积。由于故障后短时间内直流电流持续增大，换相角的增大会使得换相过程结束时刻的直流电流更大，进而导致需求换相面积增加，使得换相角进一步增加。但对于换相过程后的关断过程而言，换相角增大后，关断角必然减小，当换相角增大到一定程度使得关断面积小于最小关断面积时，换相失败就发生了。

此外，故障后等效换相电感也会变化，对需求换相面积产生影响；不对称故障下的换相电压偏移则会对实际换相面积产生影响。故障程度不严重时，电压跌落程度不深，直流电流上升较慢、较少，使得控制系统有一定的调节裕量与响应时间。但由于CIGRE 模型中定关断角控制响应不够迅速，所计算的触发角指令也不够准确，系统发生换相失败的概率仍较大。此时，如采取合适的控制，较快地给出较为准确的触发角指令，将提升换相失败抑制成功的概率。如何在提前触发控制中计及故障后换相电压、直流电流、换相电压偏移、换相角和等效换相电感的变化是实现精准提前触发的关键，也是实现换相失败抑制的关键。

2 基于电压换相面积预测的换相失败抑制

在正常运行期间，逆变侧各电气量波形如图2所示。图中，i1至i6分别为通过晶闸管VT1至VT6的电 流，ia、ib、ic分 别 为 变 压 器 阀 侧A 相、B 相、C 相 电流，IdN为额定直流电流。

图2 逆变器换相过程波形Fig.2 Waveforms of commutation process of inverter

2.1 计算当前换相过程的实际换相面积

本文利用触发脉冲和变压器阀侧电流特征分别检测换相开始时刻和换相结束时刻。以VT6向VT2换相为例，通过检测VT2的触发脉冲是否发出得到换相开始时刻t1。在换相结束时刻，流过VT6的电流i6下降至0，同时，变压器阀侧电流ib也从正的额定值下降至0。通过检测ib是否小于阈值（0.01 p.u.）来得到换相结束时刻t2。对于其他换相过程，则检测相应将要开通阀臂的触发脉冲作为换相开始时刻信号，检测相应将要关断阀臂所对应的特征阀侧电流是否小于阈值作为换相结束时刻信号。对于确定的变压器绕组接线方式，其换相过程的阀臂电流与阀侧电流的特征是确定的。

精确的实际换相面积计算公式已由式（5）给出，其几何意义即为图2 中曲边梯形BCEF的面积。在此，以图2 中梯形BCEF的面积来等效曲边梯形BCEF的面积，通过测量换相开始和结束时刻的换相电压来估算实际换相面积，如式（8）所示。

式中：CE、BF、BC分别为梯形BCEF的边长。

定义该估算方法的误差ε为：

以CIGRE 标准模型中正常换相过程为例，取α=142°、μ=23°、γ=15°，根据式（9），此时该方法误差ε1=1.36%。当故障后触发提前时，换相角增大，关断角减小，取α=135°，μ=35°，γ=10°，此时误差ε2=3.13%。误差均不大，说明该估算方法具有可行性。同时，还可以通过补偿估算实际换相面积来降低其误差，有

式中：A′fact.est为补偿后估算的实际换相面积；kc为补偿系数，利用正常换相时的ε1计算，kc=1/（1-ε1）。

2.2 预测下一换相过程的需求换相面积

考虑到换相过程时间较短，且交/直流侧均存在电感，可认为在故障发生后直到换相失败发生前直流电流变化率基本不变，即可实现利用当前直流电流及其变化率来预测较短时间内某一时刻的直流电流，预测直流电流Idpre(t) 的表达式为：

式中：t为预测时刻；t0为当前时刻；kId（t0）为当前时刻直流电流变化率。

根据式（3）可知，任何换相过程的实际换相面积都等于需求换相面积，通过当前换相过程实际换相面积的估算与直流电流的预测可以实现下一换相过程需求换相面积的预测。

若故障已发生，等效换相电感变为L′c，对故障后当前换相过程有：

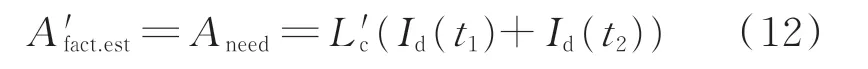
一般逆变站采用12 脉动换流器，对于Y/Y 侧的阀和Y/D 侧的阀而言，其换相需求面积表达式都是一致的，且其阀臂的触发间隔为π/6，则下一个换相过程始于当前换相过程结束后（π/6-μ）/ω，对下一换相过程的需求换相面积进行预测，有

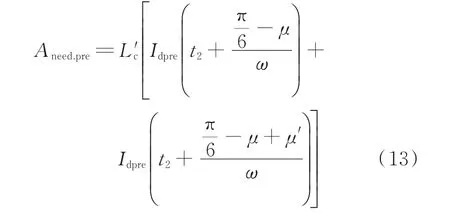
式中：Aneed.pre为下一换相过程需求换相面积预测值；μ和μ′分别为当前换相过程和下个换相过程的换相角。

由于故障后触发角可能已经减小，使得换相角有减小的趋势，且两个换相过程相距较近，换相角略微的差别对直流电流的影响较小，可取下一个换相过程的换相角与当前换相过程换相角相等，再根据式（11）将式（13）转化为：

结合式（12）和式（14）可以预测下个换相过程的需求换相面积为：

2.3 预测触发角指令的求解

对下个换相过程而言，为了保证换相过程结束后仍有足够的关断面积使得换相失败不会发生，在新的触发角指令下有：

式中：E′为故障后电压有效值；αpre为预测触发角指令；Afact.pre为下一换相过程实际换相面积的预测值，其值与Aneed.pre相等。

考虑到不对称故障情况下换相电压的过零点偏移，结合需求换相面积预测值，可以将式（16）修改为：

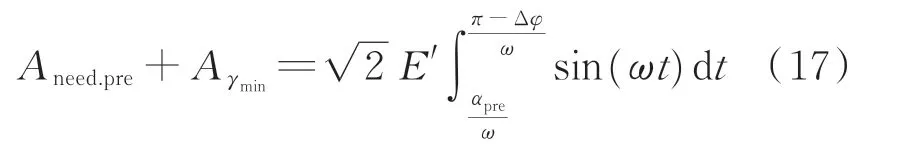
式中：Δφ为换相电压过零点偏移角度。

通过式（17）解得预测触发角指令αpre为：

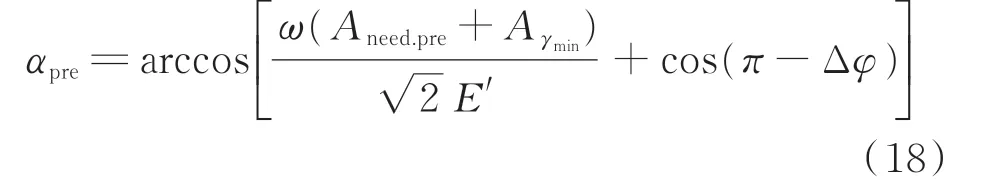
2.4 控制方法的结构框图

根据前文所述过程，引入基于电压换相面积预测的换相失败抑制方法，其控制结构如图3 所示。

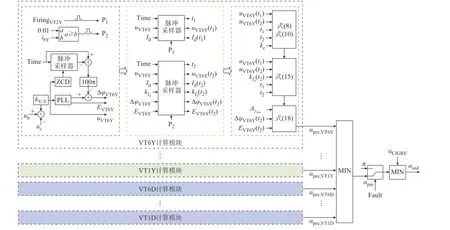
图3 换相失败预测控制结构框图Fig.3 Block diagram of commutation failure prediction control

图3 中，VT1Y 至VT6Y、VT1D 至VT6D 分别为Y 桥和D 桥换流阀；FiringVT2Y为对应换相过程将开通阀臂VT2Y 的触发脉冲信号；Time 为仿真时间；iaY、ibY、icY和iaD、ibD、icD分别为Y/Y 和Y/D 变压器阀侧电流；P1和P2分别为对应换相过程换相开始和结束时刻的检测脉冲；kY/Y为Y/Y 换流变压器变比；uk为换流阀k的换相电压，换相电压的相位θk和有效值Ek采用文献［19］中所提锁相环（PLL）方法进行检测（k=VT1Y，VT2Y，…，VT6Y，VT1D，VT2D，…，VT6D）；ZCD 为过零检测模块；MIN 为取小模块；αpre，k为对应模块计算出的预测触发角指令；Fault 为故障信号；αCIGRE为CIGRE 标准模型控制系统触发角指令；αord为系统实际触发角指令。直流电流通过滑动平均滤波后经过微分环节得到直流电流变化率。此外，通过换相电压过零时刻和额定角频率得到换相电压的正常相位，利用PLL 输出相位与正常相位做差得到换相电压偏移，然后再记录换相结束时刻的换相电压偏移为Δφk。

所提换相失败抑制方法主要步骤如下。

1）测量当前换相过程开始和结束时刻的换相电压值以及起止时刻的时间差，通过式（8）和式（10）计算当前实际换相面积。

2）测量当前换相过程起止时刻的直流电流以及换相结束时刻的直流电流变化率，通过式（11）来预测下一个换相过程起止时刻的直流电流，通过式（15）和当前实际换相面积求解下一换相过程的需求换相面积。

3）为了保证换相失败不发生，利用需求换相面积与实际换相面积相等，再结合实际换相面积和最小关断面积的关系，得到下一换相过程的预测触发角指令表达式如式（18）所示。

同样，其余换相过程的预测触发角指令也是通过上一换相过程结束时对这一换相过程的需求换相面积预测以及最小关断面积来求解的。为了保证每一阀臂都能换相成功，在12 个预测触发角指令中取最小值作为预测触发角指令的输出。在控制启动后，取CIGRE 控制系统的触发角与所提方法输出的触发角中的较小值作为最终触发角指令。除此之外，其他控制方法以及参数均与CIGRE 标准模型保持一致。此外，通过检测零序电压来判断单相故障，基于abc/αβ坐标变换来检测三相故障［20］，以生成故障信号Fault。

3 仿真验证与分析

3.1 仿真模型

本文以CIGRE Benchmark 模型为测试系统［21］，搭建了2.4 节中提出的控制模块。

3.2 交流故障下换相失败抑制性能测试

为了验证本文所提方法对测试系统逆变侧换相失败的改善情况，以交流系统单相接地故障、三相接地故障、两相接地故障和两相短路故障为典型案例进行测试。设置故障持续时间为0.05 s，以0.00 1 s为步长，故障发生时间为3.000 s 至3.009 s。对于A相单相接地故障，接地电感设为0.50～0.98 H；对于三相接地故障，接地电感设为0.94～1.30 H；对于两相接地故障，接地电感设为0.88～1.34 H；对于两相短路故障，接地电感设为1.96～2.84 H。仿真结果如图4 所示。

由图4 可知，所提方法能够在各类故障发生时有效降低换相失败发生的概率。整体来说，不对称故障的抑制效果略微差于三相接地故障的抑制效果，其原因是CIGRE 标准模型中逆变侧交流系统短路比（SCR）为2.5，为弱交流系统。当发生单相接地故障或两相接地故障时，其换相电压畸变比三相故障下更严重。由于本文所提方法抑制效果在一定程度上依赖于换相面积的计算是否准确，而换相面积计算的准确与否又极大地取决于换相电压波形是否仍然保持为正弦波，所以在换相电压畸变较为严重的情况下所提方法的计算准确性有待进一步提升。同时，不对称故障下换相电压偏移的准确测量对所提方法也有一定影响。此外，在不对称故障下，对于换相过程及距离换相开始时刻较近的故障而言［17］，本文所提方法效果一般。

图5（a）为3.000 s 时发生A 相接地故障、接地电感为0.8 H 情况下系统相应电气量波形；图5（b）为3.000 s 时发生三相接地故障、接地电感为1.0 H 情况下系统相应电气量波形。由图5 可以看出，CIGRE标准模型控制策略中的定关断角控制器要在关断角测量更新后通过比例-积分（PI）控制更新触发角指令，而本文所提方法在每一换相过程结束时就更新了触发角指令，比定关断角控制器更早。此外，结合本文所提触发角指令计算方法，其指令值也更加精准，故能比CIGRE 标准模型控制策略更好地抑制换相失败。

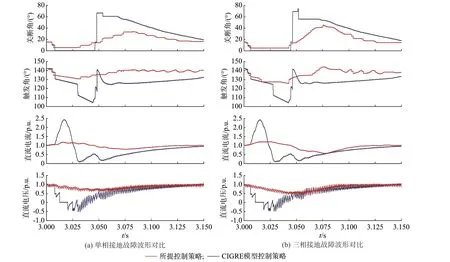
图5 单相和三相接地故障下波形对比Fig.5 Comparison of waveforms under single-phase and three-phase grounding faults

4 结语

本文基于换相电压时间面积理论提出了一种基于电压时间换相面积计算与预测的换相失败抑制方法。该方法考虑了故障后直流电流的变化、等效换相电感的变化、换相电压的变化以及不对称故障下换相电压的过零点偏移，对预测触发角的计算更加精准。该方法具有清晰的物理意义，响应快速，不需要进行参数整定。最后，在PSCAD/EMTDC 中利用CIGRE 标准模型对所提换相失败抑制方法的性能进行了测试。结果表明，所提方法能够有效提高各类故障下系统的换相失败抑制能力。此外，由于已建高压直流工程检测装置采样频率不够高，所提方法测量所得换相开始和结束时刻仍存在一定误差。所提方法具有一定的复杂性，对处理器性能要求较高，实际工程应用效果还有待进一步验证。