计及换流器间动态交互的中压直流配电系统控制参数设计

朱 琳，赵学深，郭 力，李霞林，邓占锋，王成山

（1. 智能电网教育部重点实验室（天津大学），天津市 300072；2. 天津市智慧能源与信息技术重点实验室，天津市 300072；3. 全球能源互联网研究院有限公司，北京市 102209）

0 引言

随着电动汽车、数据中心等负荷的迅猛增加，以及光伏发电、燃料电池等可再生能源的快速发展，中压直流（medium-voltage DC，MVDC）配电系统具有能源效率高、配电容量大、供电质量好等优点，引起了广泛关注［1-2］。恒功率负荷（constant power load，CPL）的负电阻特性容易使MVDC 配电系统出现稳定性问题。合适的控制参数虽然能够充分保证系统的动态稳定性，但各换流器之间存在的动态交互又使得系统的控制参数设计变得非常复杂［3-5］。因此，在计及换流器间动态交互的前提下，如何合理设计MVDC 配电系统的控制参数将成为未来的研究方向。

适用于MVDC 配电系统的常规控制参数设计方法通常包含2 步。第1 步：基于单台换流器在其独立运行时（简称单换流器场景）的开环和闭环传递函数，并利用频域分析法设计其控制参数［6-9］。文献［6］介绍了一种适用于单换流器场景的控制参数设计方法，但没有考虑负荷特性；文献［8-9］则建立了计及阻性负荷特性的开环和闭环传递函数，并根据电流控制环和电压控制环的动态性能指标设计了控制参数。第2 步：基于直流系统的阻抗模型［10-11］、状态空间矩阵［8-9，12］或开关模型［5］，利用数学解析、根轨迹或调试经验等方式再次调整控制参数，使得系统动态达到预期目标［10-14］。文献［10］在忽略电流控制参数的前提下，建立了直流系统二阶阻抗模型，分析了电压控制参数对系统动态稳定性的影响。文献［12］通过参与度分析确定了与电压动态特性强相关的状态变量，但没有给出定性定量设计系统控制参数的方法。当单换流器场景设计的控制参数不能满足系统稳定性需求时，往往会通过附加新型控制器的方式来恢复直流系统稳定性［15-19］，而并非通过优化系统的原有控制参数来解决该问题。综上所述，阻抗模型、状态空间矩阵或开关模型不仅难以直观揭示换流器间动态交互的机理，而且难以提供控制参数设计所需要的开环传递函数［18-19］。

针对上述问题，本文开展了计及换流器间动态交互的MVDC 配电系统控制参数设计工作。以采用下垂双环控制的MVDC 配电系统为例，针对各换流器的电流控制环、电压控制环和下垂控制环，逐步建立了计及换流器间动态交互的开环和闭环传递函数。基于各控制环的开环和闭环传递函数，本文提出一种计及换流器间动态交互的MVDC 配电系统控制参数设计方法，能够定性定量设计MVDC 配电系统的动态特性。在PLECS 软件中搭建了MVDC配电系统开关模型，对本文所建传递函数及所提设计方法的有效性进行了验证。

1 计及换流器间动态交互的传递函数模型

本文以典型的采用下垂双环控制的MVDC 配电系统为研究对象，其拓扑结构如图1 所示。MVDC 配电系统共包含n个电压源换流器（voltage source converter，VSC）和m个CPL。以图1 所示的MVDC 配电系统为例，本章将逐步建立计及换流器间动态交互的开环和闭环传递函数，共包含系统中各换流器的电流控制、电压控制和下垂控制环节。图中：Vrefn和Vdn分别为第n台VSC 的电压参考值及下垂控制环输出信号；Irn和In分别为第n台VSC 的电流内环输出信号和输出滤波电感电流；Dn和Cfn分别为第n台VSC 的占空比和输出滤波电容；Rcm和Lcm分别为第m条电缆线路的线路电阻和线路电感；CLfm为第m个CPL 的输入滤波电容。为方便理解，其余变量含义将在后文予以说明。

图1 MVDC 配电系统拓扑结构Fig.1 Topology of MVDC distribution system

1.1 电流内环传递函数模型

本节将建立计及换流器间动态交互的电流控制环的开环和闭环传递函数，为后续开展MVDC 配电系统中各换流器的电流控制参数设计提供模型支撑。

系统主导振荡频率的选取会受到电缆线路引入的系统固有振荡频率的影响，但当2 个振荡频率之间相差5 倍频时，电缆线路的影响就可以被忽略［18-19］。受篇幅所限，在后续分析中将忽略电缆线路的影响（考虑电缆线路影响的MVDC 配电系统控制参数优化设计将另文阐述）。由图1 可知，第x台VSC 的开环传递函数Gvdx（s）表达式为：

式中：Vsx和Lfx分别为第x台VSC 的输入直流电压和 输 出 滤 波 电 感；Ceq、Leq和Req分 别 为MVDC 配 电系统的等效滤波电容、等效滤波电感和等效电阻。

基于传递函数Gvdx(s)，可得第x台VSC 电流控制环的开环传递函数Gidx(s)表达式为：

定义Giv(s)=Ceqs-1/Req。由式(2)可知，相对于单换流器场景时电流控制环的开环传递函数而言，传递函数Gidx(s)计及了系统中各换流器间的动态交互：不仅计及了第x台VSC 的滤波参数，而且计及了其他VSC 的滤波参数。

定 义 第x台VSC 的 电 流 控 制 器Gicx（s）表 达式为：

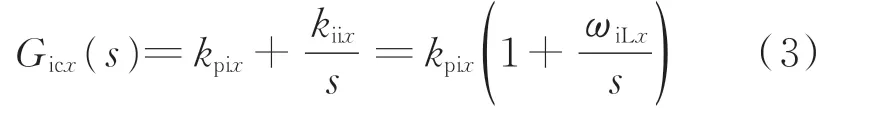
式中：kpix和kiix分别为电流控制器Gicx（s）的比例系数和积分系数；ωiLx为电流控制器Gicx（s）的积分频率。定义ωicx为第x台VSC 的电流控制回路增益的穿越频率，而ηix则定义为ωiLx与ωicx间的比值。

第x台VSC 的电流控制回路增益Tiix（s）和闭环传递函数Giix（s）分别为：

由式（5）可知，相对于单换流器场景时的电流闭环传递函数而言，传递函数Giix（s）计及了系统中各换流器间的动态交互：不仅计及了第x台VSC 的滤波参数及电流控制参数，而且计及了其他VSC 的滤波参数。此外，本文所建立的计及换流器间动态交互的电流控制环的开环和闭环传递函数的零极点数量，完全等于单换流器场景时电流控制环的开环和闭环传递函数的零极点数量，详情如表1 所示。

表1 计及换流器间动态交互的传递函数的零极点数Table 1 Number of zeros and poles of transfer function considering dynamic interaction between converters

1.2 电压外环传递函数模型

本节将建立计及换流器间动态交互的电压控制环的开环及闭环传递函数，为后续开展MVDC 配电系统中各换流器的电压控制参数设计提供模型支撑。

由图1 和式（5）可知，计及换流器的电流控制环后，第x台VSC 的电压控制开环传递函数Givdx（s）表达式为：

定 义 第x台VSC 的 电 压 控 制 器Gvcx（s）表 达式为：

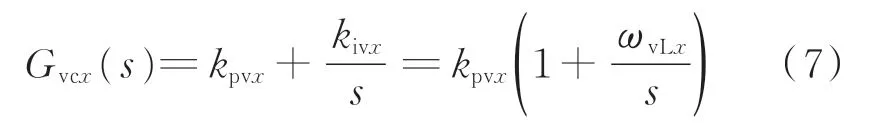
式中：kpvx和kivx分别为电压控制器Gvcx（s）的比例系数和积分系数。定义ωvcx为第x台VSC 的电压控制回 路 增 益 的 穿 越 频 率，而ηvx则 定 义 为ωvLx与ωvcx间的比值。

第x台VSC 的 电 压 控 制 回 路 增 益Tvivx（s）和 闭环传递函数Gvivx（s）分别为：

由式（9）可知，相对于单换流器场景时电压控制闭环传递函数而言，传递函数Gvivx（s）计及了系统中各换流器间的动态交互：不仅计及了第x台VSC 的滤波参数、电流和电压控制参数，而且计及了其他VSC 的滤波参数和电流控制参数。此外，本文所建立的计及换流器间动态交互的电压控制环的开环和闭环传递函数的零极点数量，完全等于单换流器场景时电压控制环的开环和闭环传递函数的零极点数量，详情如表1 所示。

1.3 下垂控制传递函数模型

本节将建立计及换流器间动态交互的下垂控制环的闭环传递函数，为后续开展MVDC 配电系统中各换流器的下垂控制参数设计提供模型支撑。

由 图1 可 知，第x台VSC 的 下 垂 控 制 器Vdx（s）表达式为：

式中：IL为所有恒功率负荷电流ILx的累加和；V为MVDC 配电系统的直流母线电压；k为下垂系数；Kdsx为第x台VSC 的下垂系数，详情如式（11）所示。

计及换流器的电流控制环、电压控制环和下垂控制环后，第x台换流器的电压控制闭环传递函数Gvivrx(s)为：

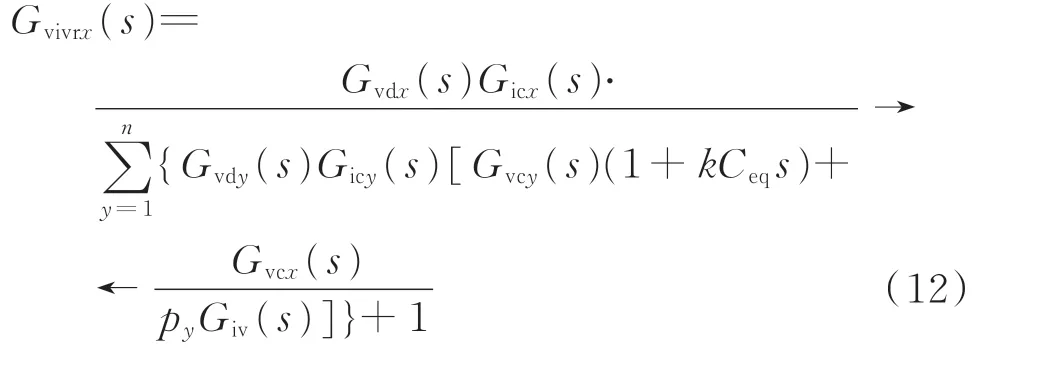
2 MVDC 配电系统控制参数设计方法

基于第1 章所建立的计及换流器间动态交互的开环和闭环传递函数模型，本文提出了一种计及换流器间动态交互的MVDC 配电系统控制参数设计方法，设计流程详情如附录A 图A1 所示。基于对下垂控制、电压外环控制和电流内环控制的信号传递顺序的考虑，该控制参数设计方法共包含3 个步骤：第1 步，设计各换流器电流内环的比例-积分（PI）控制参数；第2 步，设计各换流器电压外环的PI控制参数；第3 步，设计各换流器下垂控制环的下垂系数。

2.1 电流内环控制参数设计

计及换流器间动态交互的MVDC 配电系统控制参数设计方法的第1 步，就是要对各换流器依次进行电流内环的PI 控制参数设计，详情如附录A 图A2 所示。

为方便表述，本文按照MVDC 配电系统中各换流器的编号顺序，依次设计各换流器电流内环的PI控制参数（各换流器的先后设计顺序对最终结果无影响）：首先，设计第1 台换流器电流内环的PI 控制参数；然后，设计第2 台换流器的电流控制参数；按此顺序，最后设计第n台换流器的电流控制参数。下面以第x台换流器为例，详细介绍其电流控制参数的推荐设计方案：首先，建议按照穿越频率ωicx取值为换流器开关频率的10%来设计电流内环的比例系数kpix；然后，建议按照ηix取值为0.1 来设计电流内环的积分系数kiix，进而积分环节的kiix就不会影响ωicx的最终取值。

待MVDC 配电系统中所有换流器均设计完成其电流内环的PI 控制参数后，再进行MVDC 配电系统控制参数设计方法的第2 步：设计MVDC 配电系统中各换流器电压外环的PI 控制参数。

2.2 电压外环控制参数设计

计及换流器间动态交互的MVDC 配电系统控制参数设计方法的第2 步，就是要对各换流器依次进行电压外环的PI 控制参数设计，详情如附录A 图A3 所示。

为方便表述，本文按照MVDC 配电系统中各换流器的编号顺序，依次设计各换流器电压外环的PI控制参数（各换流器的先后设计顺序对最终结果无影响）：首先，设计第1 台换流器电压外环的PI 控制参数，详情如附录A 图A3（a）所示；然后，设计第2 台换流器电压外环的PI 控制参数，详情如图A3（b）所示；按此顺序，最后，设计第n台换流器电压外环的PI 控制参数，详情如图A3（c）所示。下文以第x台换流器为例，详细介绍其电压控制参数的推荐设计方案。若要实现零极点抵消，可按穿越频率ωvcx的取值范围选为ωicx的10%～30%来设计电压外环的比例系数kpvx；然后，建议按照ηvx的取值范围选为0.1～5.0 来设计电压外环的积分系数kivx。

由于每台换流器电压控制的闭环传递函数Gvivx（s）具有相同的特征方程，可将系统内所有换流器的闭环传递函数Gvivx（s）进行累加，并将其累加和定义为传递函数Gvivsys（s）。分析可得，传递函数Gvivsys（s）是一个包含2 个零点和4 个极点的传递函数，可用其分析系统中各换流器电压控制参数对MVDC 配电系统动态稳定性的影响。

待MVDC 配电系统中所有换流器均设计完成其电压电流双环PI 控制参数后，再进行MVDC 配电系统控制参数设计方法的第3 步：设计MVDC 配电系统中各换流器的下垂控制参数。

2.3 下垂控制参数设计

通过式（12），虽然可以分析下垂控制器Vdx（s）对第x台换流器动态特性的影响，但却无法分析所有换流器的下垂控制器对MVDC 配电系统动态特性的综合影响。

由于每台换流器下垂控制的闭环传递函数Gvivrx（s）具有相同的特征方程，可将系统内所有换流器的闭环传递函数Gvivrx（s）进行累加，并将其累加和定义为传递函数Gvivrsys（s）。由于传递函数Gvivrsys（s）是一个包含2 个零点和4 个极点的传递函数，可用其分析下垂控制参数对MVDC 配电系统动态稳定性的影响。若能够实现部分零极点的相互抵消（目的就是简化频率模型），那么就可以利用一对共轭主导极点准确设计系统动态特性。

3 理论分析与仿真验证

本文以系统参数如表2 所示的MVDC 配电系统为例，开展MVDC 配电系统控制参数的理论设计及仿真验证工作。MVDC 配电系统中存在多个辐射状连接的恒功率负荷（含电缆线路）［8］，在PLECS软件上搭建的MVDC 配电系统开环模型拓扑图（含电缆线路）如附录A 图A4 所示。另外，为与常规控制参数设计方法进行对比，附录B 表B1 给出了MVDC 配电系统中某换流器在其单独运行时的参数。

表2 MVDC 配电系统参数Table 2 Parameters of MVDC distribution system

3.1 稳定振荡频率设计与分析

在场景1 中，根据常规控制参数设计方法以及附录B 表B2 所示的具体设计依据，设计了单换流器场景的控制参数。由于单位转换关系，现给出说明：fvcx为ωvcx的 对 应 单 位 为Hz 的 变 量；γvbx为 电 压 控 制环回路增益的相角裕度，单位为（°）；fs和ζs分别为系统振荡频率和阻尼比。

附录B 图B1 所示的电压回路增益Tviv（s）的正相角裕度（γvc=25.8°），以及图2 所示均位于s域的左半平面零极点，均表明常规控制参数设计方法能够确保单换流器场景的动态稳定性。

然而，当2 台换流器（均采用常规控制参数设计方法得到其控制参数）以及恒功率负荷聚合得到MVDC 配电系统后，却出现了稳定性问题。如图2（b）所示，MVDC 配电系统在场景1 时有一对位于s域右半平面的共轭极点，表明MVDC 配电系统是不稳定的。

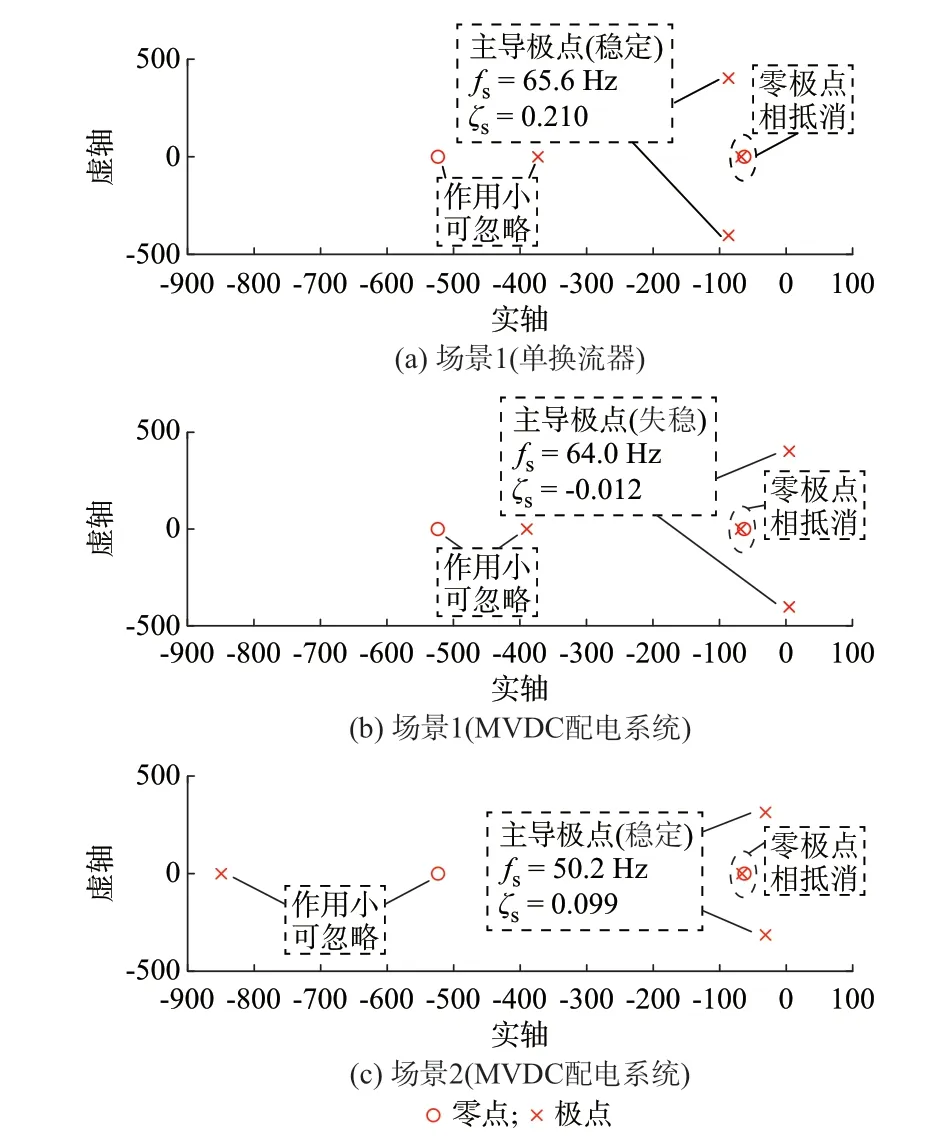
图2 场景1 和场景2 的零极点图Fig.2 Zero-pole diagram of scenario 1 and scenario 2

在场景2 中，根据所建立的计及换流器间动态交互的开环和闭环传递函数以及所提出的MVDC配电系统控制参数设计方法，并以附录B 表B3 所示的具体设计依据（与场景1 相同），设计了MVDC 配电系统的控制参数。附录B 图B1 所示的电压回路增益Tviv1（s）的正相角裕度（γvc1=1.44°），以及图2 所示均位于s域的左半平面零极点，均表明本文所建模型及设计方法能够确保MVDC 配电系统的动态稳定性。

基于PLECS 仿真软件，搭建如表2 所示的MVDC 配电系统仿真算例，以及如附录B 表B1 所示的单换流器场景算例，以验证上述理论分析的有效性。

由图3 可知，场景1 下当单台换流器的负荷功率从0.5 MW 阶跃至1 MW 时，其直流母线电压经过短暂的暂态过程后就能恢复稳定。而且，图3 中单换流器直流母线电压的振荡频率约为67.95 Hz，该值与图2（a）中的理论振荡频率65.6 Hz 基本相同，验证了理论分析的正确性。然而，当MVDC 配电系统中恒功率负荷从1 MW 阶跃至2 MW 时，MVDC配电系统的直流母线电压开始振荡发散。而且，图3中MVDC 配电系统的不稳定振荡频率为66.43 Hz，该值与图2（b）中的理论振荡频率64.0 Hz 基本相同，验证了理论分析的正确性。

图3 场景1 和场景2 的直流母线电压波形Fig.3 DC bus voltage waveforms of scenario 1 and scenario 2

场景2 下当MVDC 配电系统发生与场景1 相同的恒功率负荷扰动时，直流母线电压经过短暂的暂态过程后重新到达稳态。并且，暂态过程的振荡频率为49.57 Hz，该值与图2（c）中的理论振荡频率50.2 Hz 基本相同，验证了理论分析的正确性。

由上述理论分析及仿真验证可知，本文所建立的计及换流器间动态交互的开环和闭环传递函数以及本文所提出的MVDC 配电系统控制参数设计方法，能够有效保证整个MVDC 配电系统的动态稳定性。

3.2 振荡频率宽范围设计能力

本节将介绍所建传递函数及所提控制参数设计方法的系统振荡频率宽范围设计能力，详情如场景3、场景4 和场景5 所示。场景3 至场景5 的控制参数设计方法分别如附录B 表B4 至表B6 所示。

由附录B 图B2 可知，场景3 至场景5 的传递函数Tviv1（s）的穿越频率fvc1会随着fvcx预设值（分别为10、30、40 Hz）的 增 大 而 逐 渐 增 大（分 别 为16.5、42.3、53.1 Hz）。在很多研究文献中ηvx通常取值为0.1，而本文想要通过部分零极点的相互抵消，进一步达到仅由一对共轭极点就能描述MVDC 配电系统动态特性的目的。因此在本文中ηvx取值为1 或1.25，这也就是附录B 图B2 中fvcx实际值不等于其预设值的原因所在。由图4 可知，正是由于部分零极点的相互抵消（虽然部分零极点相近但不完全相等，但消去此对零极点对模型准确度产生的影响可以被忽略），场景3 至场景5 的系统振荡频率fs均可分别由其一对共轭极点计算得到，分别为10.5、36.3、48.9 Hz。

图4 场景3、场景4 和场景5 的零极点图Fig.4 Zero-pole diagram of scenario 3,scenario 4 and scenario 5

为验证上述振荡频率理论设计的有效性，在PLECS 仿真软件上对场景3 至场景5 进行了时域仿真，直流母线电压波形如图5 所示。图中，场景3 至场景5 的直流母线电压时域振荡频率分别为10.39、33.46、47.06 Hz，均与图4 中的理论设计值基本一致。

图5 场景3、场景4 和场景5 的直流母线电压波形Fig.5 DC bus voltage waveforms of scenario 3, scenario 4 and scenario 5

由上述仿真结果可知，本文所建传递函数及所提控制参数设计方法的系统振荡频率宽范围设计能力得以验证。另外，本文所建传递函数及所提控制参数设计方法，能够为计及约束条件（换流器占空比饱和、电缆线路引入的系统固有振荡频率等约束）的MVDC 配电系统全局最优目标设计提供便利：时域仿真（基于PLECS 软件）所体现的系统振荡频率fs（分别为10.39、33.46、47.06 Hz）与理论设计（基于MATLAB 软件）得出的主导极点（分别为10.5、36.3、48.9 Hz）基本一致，为MVDC 配电系统全局最优目标设计节约了大量时间。

4 结语

本文以典型的采用电压电流双环控制的MVDC 配电系统为例，开展了MVDC 配电系统控制参数设计的研究工作，主要贡献和结论如下：

1）针对MVDC 配电系统中各换流器的电流控制环、电压控制环和下垂控制环，逐步建立了适用于各控制环节的计及换流器间动态交互的开环和闭环传递函数。相对于单换流器场景的各控制环节而言，本文所建立的计及换流器间动态交互的开环和闭环传递函数的零极点数量均没有发生改变。

2）计及换流器间动态交互的电压控制闭环传递函数，能够非常直观地揭示其他换流器的电压控制参数对某换流器动态特性的影响机理。

3）基于所建立的计及换流器间动态交互的传递函数，本文提出了一种计及换流器间动态交互的MVDC 配电系统控制参数设计方法，该方法共包含3 步：第1 步，设计所有换流器的电流控制参数；第2步，设计所有换流器的电压控制参数；第3 步，设计所有换流器的下垂控制参数。

4）基于计及换流器间动态交互的MVDC 配电系统控制参数设计方法，不仅能够定性定量地设计系统动态特性（振荡频率及阻尼比），而且能够通过设计各换流器的电压控制参数，使得各换流器间具有不同的动态特性。

本文方法对各换流器滤波参数的准确性要求较高，当滤波参数实际值与理论值出现偏差时，系统理论设计的动态特性与实际动态特性间就会存在差异。另外，当遇到某台换流器突然投入或切除等情况时，系统的动态特性也会偏离预期设定状态，这时也需要重新整定系统控制参数。在MVDC 配电系统中，换流器与电缆线路间也会存在动态交互，并且该动态交互可能会影响系统稳定性，严重时甚至会造成系统失稳，故计及电缆线路影响的系统控制参数优化设计将是未来的研究方向之一。

本文得到了天津大学李鹏飞博士研究生在论文逻辑设计方面的鼎力帮助，以及天津大学卢浩硕士研究生在论文内容校核方面的帮助，特此感谢！十分感谢审稿专家提出的中肯意见！

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。