下垂并网逆变器网络的慢同调与聚合方法

刘鸿鹏，刘佳耕，张 伟，陈继开，曹云峰

（1. 现代电力系统仿真控制与绿色电能新技术教育部重点实验室（东北电力大学），吉林省吉林市 132012；2. 国网新疆电力有限公司营销服务中心，新疆维吾尔自治区乌鲁木齐市 830001）

0 引言

由于间歇性且波动的可再生能源大规模接入电力系统，电力系统面临着更多的复杂性和不确定性，给系统稳定性带来了很大影响［1-3］。在大型电力系统中进行动态研究时，同调等值法常被用于减少系统仿真计算量，得到的等值项充分保留了整个系统的动态特性［4-6］，故可用于研究故障等运行条件下的暂态稳定性。同调分群算法也可用于主动解列控制等情况［7-8］。

目前，基于逆变器的分布式发电网络降阶模型的研究主要采用基于模型的方法。文献［9］根据扰动时转子偏差角度判别的方法，识别虚拟同步机控制的电压源型逆变器。文献［10］提出一种基于哈密顿作用的方法，采用暂态条件下电流的偏差关系识别同调性。文献［11］将这种方法用于识别两级光伏系统模型的同调性。但以上两种方法均需要比较暂态条件下参数的变化量来进行同调识别，对于电源数量较多的分布式发电网络，其计算速度较慢。文献［12］将广义特征值摄动的方法应用于并网逆变器的同调性识别，该方法能够保留原网络的负载母线和网络结构，但不能应用于混合电源（逆变器与发电机）的同调性识别。

文献［13］对PQ控制的逆变器和下垂控制的逆变器分别建立降阶模型，但该方法只是简单假设相同控制的逆变器具有同调性。文献［14］基于逆变器到电网的电气距离，采用k均值算法来寻找同调区域，但需要假设电气距离相同的逆变器动态一致，存在很大的局限性。

除此之外，还有一些基于测量的方法，其动态等值项主要通过数据集导出。文献［15］采用黑箱的方法，将输入输出导入MATLAB 中以确定等值模型参数。文献［16-18］通过灰箱方法提出了有源分布式网络的动态等值模型。虽然这种基于测量的方法无需模型的拓扑结构，但它受扰动位置影响较大，测量容易受到噪声和数据质量问题的影响［19-20］。

而此前应用于同步发电机的慢同调算法［21-22］，主要根据弱连接性质识别具有相同振荡频率的电源，具有计算速度快、不受扰动大小影响的特点。本文提出一种基于改进慢同调算法的同调等值方法，创新点具体体现在以下4 个方面：

1）将之前仅用于同步发电机的慢同调算法应用于下垂控制逆变器，扩展了慢同调算法的应用范围；

2）针对传统慢同调算法忽略了同步发电机阻尼系数的问题，提出了考虑下垂控制逆变器中阻尼影响的改进慢同调算法，提升了慢同调算法结果的准确性；

3）针对传统慢同调算法在某些情况下准确性差的问题，将模糊C均值（fuzzyC-means，FCM）空间聚类算法应用于慢模式对应的特征子空间基矩阵，分析验证了所提方法的有效性；

4）针对传统聚合方法［9-13］存在的忽略控制方程中解耦项对等值参数影响的问题，详细分析了解耦项和虚拟阻抗与其控制参数的关系，并据此求取相应的等值参数。

最后，通过PLECS 仿真平台验证了不同故障下等值模型与详细模型的一致性。

1 系统模型

1.1 逆变器控制模型

1.1.1 下垂控制

下垂控制是模仿同步发电机的调速器，在常规电力系统中，同步发电机将根据其调速器下垂特性通过降低频率来分担负载的功率。首先，通过逆变器输出电压和输出电流计算三相瞬时有功功率P～ 和瞬时无功功率Q～，并经过低通滤波器可以得到有功和无功功率。

式中：τp为低通滤波时间常数。

本文以感性网络为例进行分析，故采用感性下垂方程计算电压和频率如式（2）所示。通过调节逆变器输出电压的相位和幅值，就能够分别调节有功和无功功率的大小。此外在逆变器并网时，由于阻抗压降的作用，即使电网为额定值，输出的无功功率也不等于所期望的QN，所以无功下垂方程采用比例-积分（PI）控制。

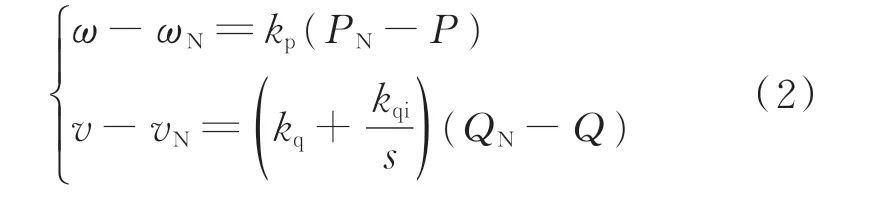
式中：ω和ωN分别为逆变器参考角频率和额定角频率；PN和QN分别为额定有功和无功功率；vN为额定电压；v为逆变器参考电压幅值；kp为有功功率下垂方程的增益系数；kq和kqi分别为无功功率下垂方程的比例和积分系数。通过参考电压幅值v和角频率ω计算用于电压环的dq旋转坐标系下的参考电压。

1.1.2 电压电流控制

电压控制和电流控制均采用PI 控制器，并采用如式（3）和式（4）所示的反馈项进行解耦［23］。此外，为抑制逆变器并联产生的环流加入了感性虚拟阻抗。

1.2 LCL 滤波网络模型

逆变器的状态方程是在各自参考框架下的表示形式，因此要将逆变器连接到整个系统，需要将输出变量转换为公共参考系［13］。变换角度δ为：

式中：vpcc，d为d轴旋转坐标系下的节点电压；vl，d为d轴旋转坐标系下的逆变器桥臂输出电压；ωcom为公共参考系坐标轴角频率。

根据图1 所示的三相逆变器的LCL 滤波结构，可以得到LCL 滤波d轴状态变量的动态方程如式（6）所示，q轴同理。

图1 下垂控制三相并网逆变器单线图Fig.1 Single-line diagram of three-phase grid-connected inverter with droop control

2 适用于逆变器的慢同调与聚合方法

2.1 慢同调模型

电力系统的非线性机电模型通常为常规发电机的二阶动态方程，是研究暂态稳定性的最简单模型。

式中：δ′为发电机转子角度；ω′为发电机角速度；Pm为原动机输入的机械功率；Pe为发电机输出的电磁功率；H为发电机惯性常数；d′为发电机阻尼常数；Ω为额定角频率。

通过表征其振荡频率和初始相位角来反映发电机转子的摆动状态，发电机的输出功率表示为：

式中：E为发电机暂态电抗后的电压且假设其为定值；x′d为暂态电抗；V为母线电压幅值；θ′为母线电压相角。

慢同调模型的建立主要由以下3 个步骤组成：1）化简网络为只有发电机内部节点的网络［24］，计算导纳矩阵；2）忽略转子运动方程的阻尼系数；3）线性化动态方程并计算同步转矩系数K的值。对于包含n台发电机的系统，其慢同调模型为：

式中：M为包含惯性时间常数的对角矩阵；符号Δ 代表此变量与特定稳态操作点的偏差。

该模型使用以下假设［21］：发电机的同调群与扰动的大小无关。因此，可以通过考虑线性化系统模型来确定同调性。同调群与发电机模型中的细节量无关，故考虑了传统的同步电机模型，而忽略了励磁、无功功率或电压控制。

2.2 适用于下垂控制逆变器的慢同调模型

慢同调算法产生于区域间模式。在振荡频率下发电机不同的同调群之间的摆动模式要比同调群内的局部模式慢得多，即同调区域内的连接较强，而区域间的传输线阻抗较高、负载较重或连接较少。这些系统属性允许使用奇异摄动来显示区域间模式和局部模式的时间尺度差异，从而产生基于特征向量的算法来识别同调发电机。

该算法主要分为4 个步骤：1）选择g个分群数，建立慢同调模型；2）计算M-1K的特征值，得到g个最小特征值对应的特征子空间基矩阵；3）将高斯消去法应用于特征子空间基矩阵找到参考发电机；4）构造分群矩阵L进行同调分群。

根据传统慢同调算法的步骤可知，应用慢同调算法的关键在于建立慢同调模型并计算同步转矩系数K。根据2.1 节所述，该模型在逆变器网络中的应用受到两个方面的限制：1）下垂控制逆变器没有类似于转子运动方程的二阶动态方程；2）传统慢同调算法没有考虑阻尼的影响。因此，建立下垂控制并网逆变器的慢同调模型，首先需要建立与式（7）类似的二阶动态方程。

根据系统特征值的模值可知，下垂控制逆变器为三时间尺度模型，其中滤波网络的LCL 部分与电压电流控制所属的时间尺度相对较短［25］。根据奇异摄动理论，对于多时间尺度的系统，可以将系统的动态过程分为快时间尺度和慢时间尺度，并且令ε=diag{ε1，ε2，ε3，ε4，ε5}=diag{Kpi/Kii，Kpu/Kiu，Lf，Cf，Lt}。对于长期研究，通过设置ε=0 来忽略快动态变量，并假设忽略无功下垂控制的动态过程，保留慢时间尺度下的有功功率下垂控制与坐标变换的动态方程得到慢时间尺度模型［12］。将下垂方程进行变换，并将其线性化后得到的方程如式（10）所示。

以式（10）所示的下垂控制转换的虚拟同步机二阶动态方程作为慢同调模型，可以得到虚拟惯性时间常数T和虚拟阻尼转矩系数d：

为得到同步转矩系数K，需要推导有功功率与虚拟转子角度的关系。当逆变器并网且无滤波电感以外的线路阻抗时，根据下垂方程的推导过程可以得到有功功率的表达式如式（12）所示。

式中：Upcc为PCC 处的电压幅值，假设电压相角为零；v为逆变器参考电压幅值；Xt和Xv分别为网侧滤波电感与虚拟电感对应的电抗。

将式（12）与式（8）进行比较，可以将Xt+Xv作为虚拟暂态电抗，v作为虚拟暂态电抗后的电压，δ作为虚拟转子角度，其表达式为：

但在基于下垂控制逆变器的系统中，有功下垂系数kp的数量级通常很小，使得阻尼转矩系数较大，对于不同逆变器的转矩系数可能存在无法忽略的差值。而由于同步发电机的阻尼转矩很小，传统慢同调算法忽略了阻尼系数产生的影响，故考虑阻尼转矩的影响十分必要。

考虑阻尼的慢同调模型为：

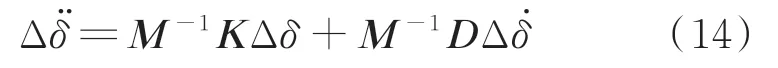
式中：D为包含各电源阻尼系数的对角矩阵。

根据动态方程可知，下垂控制逆变器的阻尼主要由M-1D决定，因此，需要在传统慢同调算法的基础上额外考虑其对系统的影响。采用设置阈值x的方法对M-1D进行额外分群，即

式中：ai为矩阵M-1D对角线中的第i个元素。可以根据经验和希望的精度来设置x，并认为同调群内的电源M-1D相同。

2.3 基于FCM 空间聚类的慢同调算法

尽管在2.2 节中已经建立了适用于下垂控制逆变器网络的慢同调模型并达到了算法的使用条件，但由于传统慢同调算法的分群结果不够准确，导致其应用于逆变器网络的效果较差。

为解决这个问题，本文在传统慢同调算法的基础上提出一个新的计算步骤。慢同调算法通过慢模式选择分群数：计算M-1K的特征值并按升序排列，寻找第r个特征值λr与第r+1 个特征值λr+1的最大间隔，选出这r个特征值即得到慢模式σa（σa=[λ1，λ2，…，λr]）。其非零模式的大小等于外部连接的总和，外部连接越弱、区域内连接越强，则该模式越接近于零。因此，分群数量的最佳选择为小于等于r。

在传统慢同调算法中，若希望的系统电源分群数为g，会采用g个最小特征值对应的分群矩阵L进行同调识别。当慢模式σa中存在r个不同的模式且g≤r时，根据分群矩阵对发电机组进行分群，能够保证系统的优化分群。但若因降阶模型准确度不够或其他情况时g＞r，则此时特征子空间基矩阵涉及慢模式外的特征值，得到的分群矩阵只是分群模式的一种，因而难以得到准确的分群结果。

因此，为改善慢同调算法的分群结果，宜采用慢模式中子模式对应的模态矩阵进行同调分群。因为特征值和特征向量对应系统的模式与模式形状，则特征子空间基矩阵的行向量对应电源不同模式下的形状，故将FCM 空间聚类算法应用于慢模式σa中子模式对应模态矩阵V的行向量。当想要的分群数g≤r时，采用g个最小特征值对应模态矩阵Vg的行向量进行聚类，得到的分群结果与传统慢同调算法一致。当g＞r时，采用慢模式σa对应模态矩阵Va的行向量进行聚类，可以将分群数为r时的分群结果进一步划分，而这也是传统慢同调算法难以达到的。这种方法的优势在于，对于不同的分群数量采用相同的模态矩阵，因而具有计算速度快的特点。除此之外，更重要的是能够产生相对准确的同调分群结果。

改进的慢同调算法具体流程如下：

1）选择分群数g，建立慢同调模型。该分群数不考虑阻尼的额外分群。

2）考虑阻尼的影响计算一次分群。比较M-1D中各元素大小，得到一次分群结果。

3）根据弱连接计算分群数r。计算M-1K的特征值并将其按升序排列，寻找λr/λr+1的最小值，得到慢模式σa。这个过程有利于确保同调分群之间弱连接，而区域内的状态牢固连接。

4）根据状态变量的给定顺序，若g≤r则计算g个最小特征值的模态矩阵Vg；若g＞r则计算慢模式σa的模态矩阵Va。

5）将FCM 空间聚类算法用于模态矩阵的行向量，根据分群数g确定第2 次分群结果。

6）在第2 次分群结果的基础上，结合一次分群再次划分得到最终结果。

2.4 聚合方法

如附录A 图A1 所示，同调识别算法得到的结果将用于聚合方法。将每个同调群等值为一个独立电源，用等值模型来代替原本的详细模型从而达到降低模型阶数的目的。

由于下垂控制已经转换为虚拟同步机动态方程的形式，因此，可以采用同步机的聚合方法，如式（16）所示。其中，下标i表示n台电源中的第i台，下标eq 表示对应变量的等值参数。

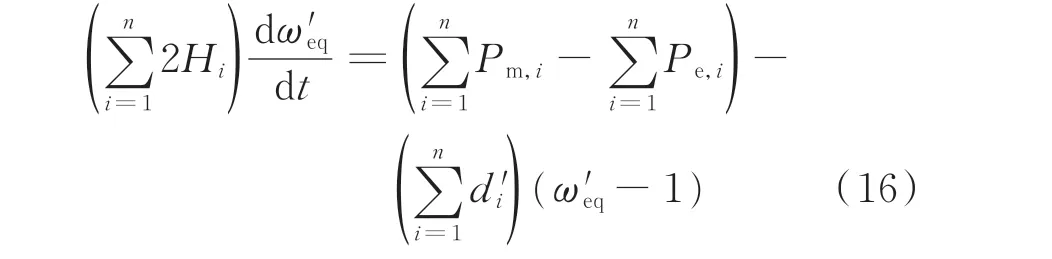
根据慢同调算法，假设同一区域内逆变器的虚拟转子角度以相同的速率变化。等值惯性时间常数、等值阻尼转矩系数、等值机械功率和等值电磁功率均为各个分群参数的和，如式（17）所示。最终，可以得到下垂方程中的等值参数，如式（18）所示，为每个逆变器下垂系数并联后的值。

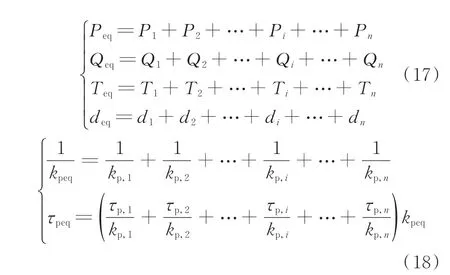
无功下垂系数与有功下垂系数采取相同的计算方法。对于电压控制参数的聚合方法，其d轴动态方程的求和如式（19）所示，等值模型动态方程如式（20）所示。

比较式（19）和式（20），因为等值模型的电压与各逆变器输出电压相同，输出电流为各逆变器之和，且使得ωiLv，iio，qi等于ωeqLveqio，q，eq，可以得到等值模型的控制参数为各逆变器之和，如式（21）所示。在线路差别不大的情况下，输出电流主要受到电源容量的影响，所以采用容量加权如式（22）所示，其中S为逆变器容量，γ为加权系数。而在线路差距明显的情况下，宜采用电流值作为加权因子。等值虚拟电感Lveq和等值滤波电容Cfeq的计算方法如式（23）所示。

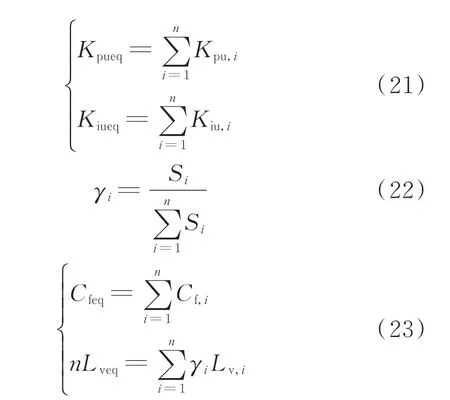
对于电流控制参数的聚合方法，其d轴动态方程的求和如式（24）所示，等值模型电流控制的动态方程如式（25）所示。

比较式（25）和式（26），同样将电源容量作为加权因子，可以得到电压控制中PI 控制参数和滤波电感Lf的聚合方法：

LCL 的其他滤波参数和线路参数的聚合方法可以看作是多个逆变器的并联：

式中：Rl和Ll分别为输电线路电阻和电感。

3 仿真分析

3.1 仿真设置

为验证模型降阶方法得到的等值模型与详细模型在仿真结果上的区别，通过两种不同的系统扰动故障情况进行验证。仿真结构采用10 台三相下垂控制并网逆变器并联，如附录A 图A2 所示。在PLECS 仿真平台中建立了详细的模型，其中所有逆变器采用相同的控制策略和结构。

各逆变器控制参数和滤波参数如表1 所示，线路电感Lline11和Lline22均为2 mH，其他线路电感均为1 mH，虚拟电感均为10 mH。本文方法适用于采用感性下垂控制的逆变器系统，并且该同调结果不会受到电压电流控制方法的影响，不同电压等级或容量的情况同样适用。此外，该同调算法不仅适用于放射网络，而且适用于网状网络，但聚合方法需要额外对电源间线路进行处理。

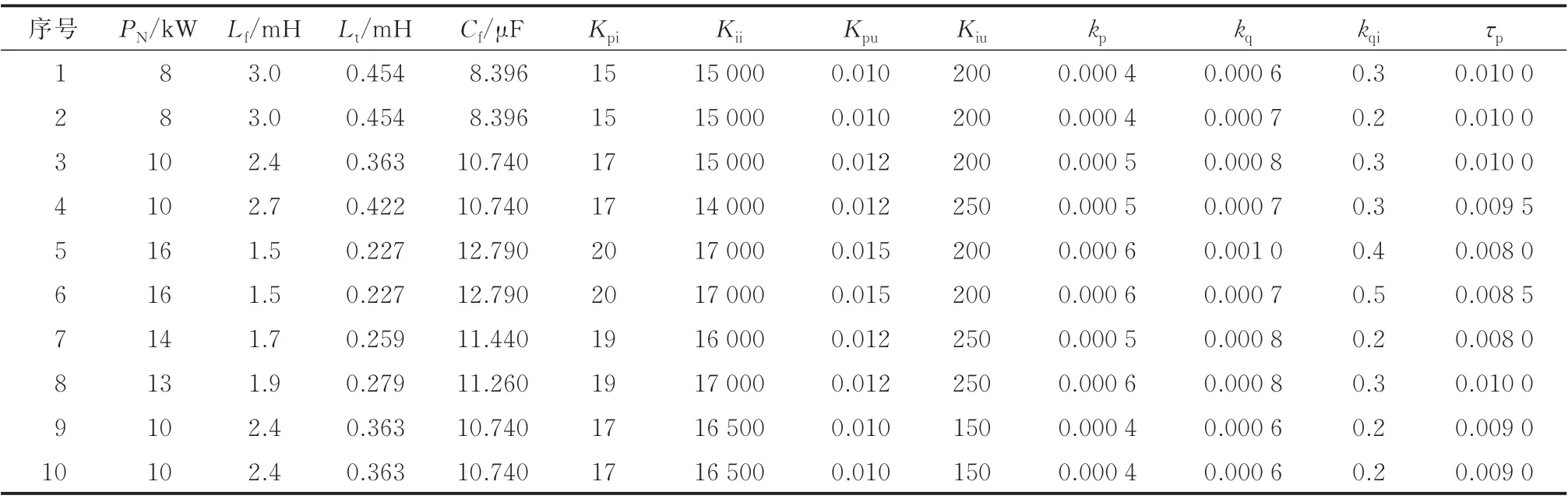
表1 10 台逆变器的详细模型参数Table 1 Detailed model parameters of 10 inverters

3.2 同调算法验证

仿真中，所有逆变器均为稳定运行。各逆变器的|M-1D| 分 别 为［125，125，100，105.3，78.13，73.53，89.29，76.92，111.11，111.11］，由于仿真中逆变器数量有限，所以将x设为12，使得逆变器1 和2分为一组，其余为一组。

系统区域之间的弱连接虽没有确切定义，但可以简单地从以下情况进行判断［26］：1）机群之间由大阻抗线路相连；2）机群内部出线度高，而机群之间出线度低。因此在线路差距较大的情况下，采用如附录A 图A2 所示的仿真模型，可以明显看出慢同调分群结果，有利于与计算结果进行验证。

通过传统慢同调算法得到的分群矩阵L见表2，特征值为［0，±j11.891 0，±j22.298 7，±j22.545 5，±j22.932 3，±j22.925 0，±j23.467 0，±j23.489 5，±j23.670 4，±j24.167 7］，所以应分为2 组，模态矩阵Va如表3 所示。

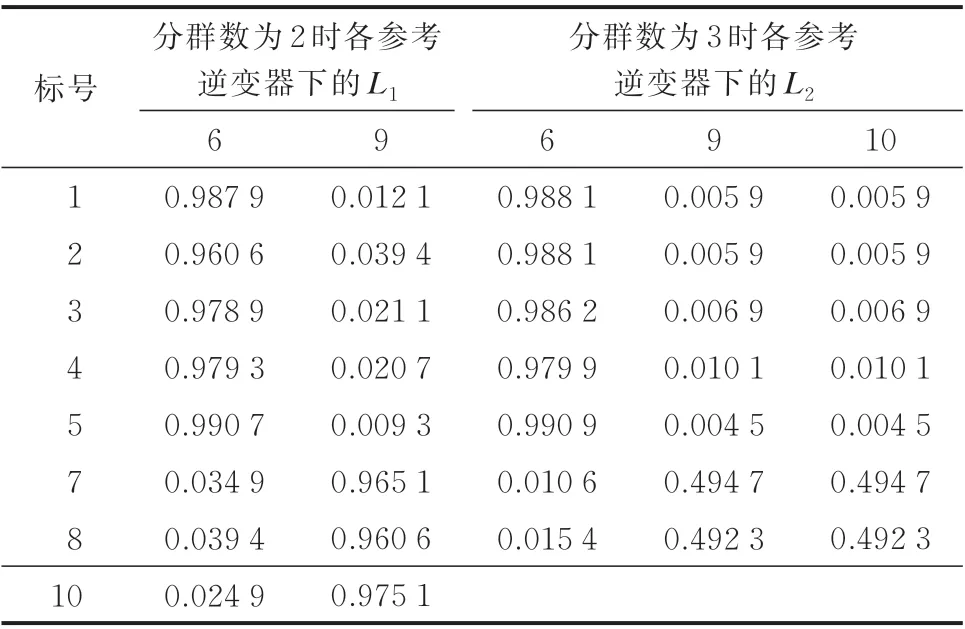
表2 分群矩阵LTable 2 Grouping matrix L

根据表2 中的L1矩阵可以看出，参考逆变器为6和9，分群结果如表4 所示，与附录A 图A2 所示的弱连接结果一致。将FCM 聚类算法应用于模态矩阵Va，当分群数为2 时结果相同，当分群数为3 时，传统慢同调分群结果如表2 中的L2矩阵，但这个结果是错误的，因为本文为了检验传统慢同调算法的准确性，仿真中设置逆变器9 与逆变器10 的所有参数均相同，应分为一组。将FCM 聚类算法同样应用于表3 的模态矩阵，选取隶属度最佳的分群结果如表4 所示。可以看出，将FCM 聚类算法应用于模态矩阵，相对于传统慢同调算法，其准确性显著提升。

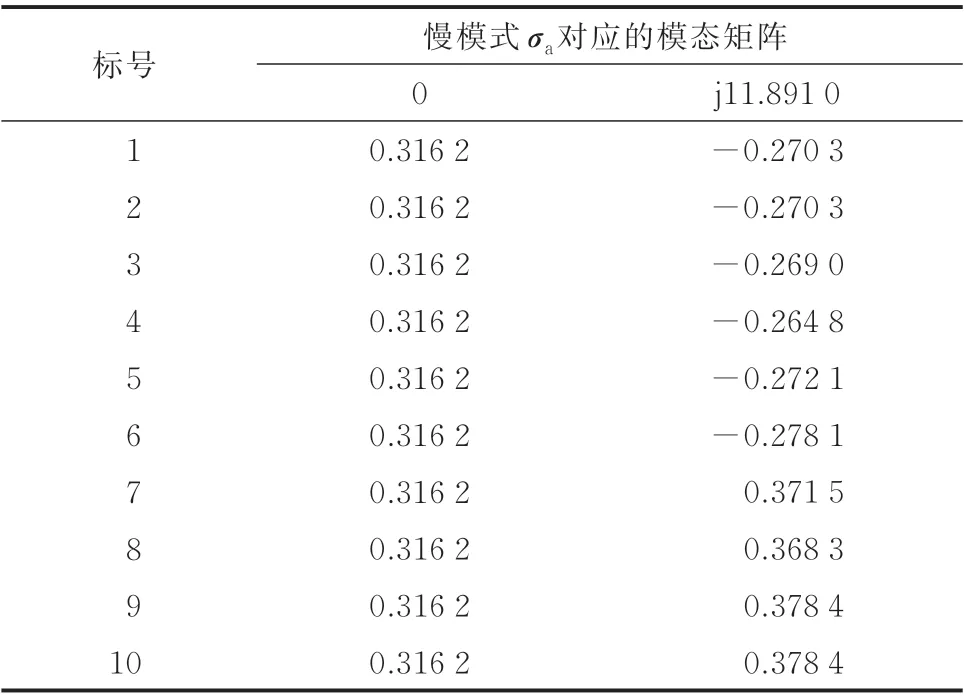
表3 模态矩阵VaTable 3 Modal matrix Va

表4 分群结果Table 4 Grouping results

在PCC 处投切负载可以得到虚拟同步机角度偏差波形如图2 和图3 所示。可以看出，基于FCM聚类算法的慢同调算法得到的同调区域中，各波形相似度较高，等值后的波形能够较好地反映详细模型。而在传统慢同调算法的同调区域中，由于逆变器9 的存在，使得等值后的波形与详细模型相差较大，不利于提高降阶模型的准确性。

图2 传统慢同调算法的分群结果Fig.2 Grouping results of traditional slow coherency algorithm

图3 改进慢同调算法的分群结果Fig.3 Grouping results of improved slow coherency algorithm

3.3 等值模型验证

3.3.1 三相短路

三相短路为电力系统中最严重的故障，以三相短路为例验证同调等值方法在大扰动下的适用性。当仿真时间为4 s 时，在PCC 处加入一个时间为0.1 s 的三相短路故障。对详细模型和等值模型仿真后得到的有功功率波形如图4 所示，无功功率波形见附录A 图A3。

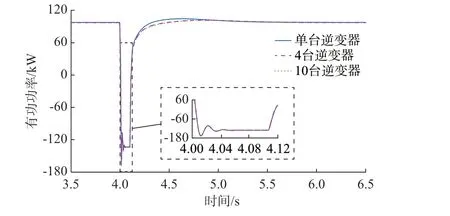
图4 三相短路故障下的有功功率波形Fig.4 Waveforms of active power under three-phase short-circuit fault

从图中可以看出，4 台逆变器等值模型的有功和无功功率曲线均显示出与详细模型几乎一致的动态特性，而单台逆变器的等值模型在故障清除后的一段时间内存在较大的误差。因此，在三相短路故障的情况下，考虑同调性降阶模型的准确度要远高于不考虑同调性的模型，并且随着分群数的增多，结果也越准确。

3.3.2 单相接地短路

单相接地短路是电力系统中最常见的故障类型，因此，本文以单相接地短路故障为例验证同调等值算法的适用性。当仿真时间为4 s 时，在PCC 处发生单相接地短路故障。对详细模型和等值模型仿真后得到的有功功率波形如图5 所示，无功功率波形见附录A 图A4。

图5 单相接地短路故障下的有功功率波形Fig.5 Waveforms of active power under singlephase grounding short-circuit fault

从有功和无功功率的响应速度来看，各波形动态几乎一致，但由于单相接地短路属于不对称故障，相对于三相短路存在更多的偏差。从图中可以看出，4 机群降阶模型有功功率的平均绝对误差为0.11%，无功功率的平均绝对误差为0.18%，可以较准确地描述详细模型的动态响应状态。而单机群降阶模型有功功率的平均绝对误差为1.29%，无功功率的平均绝对误差为2.17%。总体而言，同调等值模型在这两种扰动下均可以较准确地反映详细模型的动态特性。

4 结语

本文提出了基于改进慢同调算法的同调等值方法，并根据慢时间尺度模型以及非线性节点电压方程，将其应用范围扩展到基于下垂控制逆变器的分布式网络。改进的慢同调算法将FCM 空间聚类算法应用于慢模式对应的特征子空间基矩阵，并根据阻尼系数进行额外分群，使其更适用于阻尼较大的分布式发电网络。此外，根据慢同调区域中各逆变器状态变量的特点，提出了适用于该模型的聚合方法。同时，通过比较10 台并联下垂控制逆变器的详细模型与降阶模型在不同类型大扰动故障场景下的仿真结果，证实了同调等值算法可以有效地简化大型下垂控制逆变器网络的分析。此外，由于本文采用的同调等值算法仅适用于相同结构的电源模型，未来的工作将会集中于建立具有不同控制方式的降阶模型。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。