基于互转换Ornstein-Uhlenbeck 过程的风速仿真模型及应用

缪书唯，蒋 晨，李 丹，柯其志

（1. 三峡大学电气与新能源学院，湖北省宜昌市 443002；2. 海南电网有限责任公司海口供电局，海南省海口市 570000）

0 引言

风能具有储量巨大、分布广、成本低、开发技术成熟等优势，截至2020 年，全球风电装机容量已达742.7 GW，且中国风电装机容量位居世界前列［1］。风电场等新能源站接入高负荷密度地区，能减少区域间的碳排放不平衡量，收获可观的环境效益［2］。近年来，中国风电渗透率保持高速增长［3］，计划在“十四五”期间建设多座含风能在内的多能互补清洁能源基地，风能等非化石能源消费总量比重将提高到20%左右［4］。

对风速进行准确仿真，是对含风能发电系统进行模拟和评估的重要且基础的环节。许多文献围绕风速仿真模型展开研究，试图得到与实测风速样本特性一致的仿真风速样本。例如，文献［5］应用Johnson 分布拟合风速概率分布，进而准确计及风速概率分布特征，仿真中国甘肃某风电场的小时级风速样本。文献［6］应用混合半云模型计及两座风电场的风速相关性和概率分布特征，进而仿真中国淮安两地区的风速样本。文献［7］将风速和风向定义为风矢量，提出计及两座风电场风速风向相关性的风矢量仿真模型，并仿真荷兰两座风电场的小时级风矢量样本。文献［8］使用改进的一阶Markov 链，模拟产生具有日特性、季特性、自相关特性的小时级风速样本。文献［9］提出非参数R 藤Copula 模型，仿真产生6 处风电场的风速样本，这些仿真风速样本具有与实测风速样本类似的相关性结构。文献［10］提出改进交叉熵重要性抽样方法，该方法可计及风速波动性，用于抽样产生中国酒泉两地区的风速样本。文献［11］基于一阶连续状态Markov 链和Copula 模型产生具有自相关性的仿真风速样本，并对比仿真风速样本和实测风速样本的自相关系数曲线，发现两类曲线的变化趋势相似。文献［12］结合经验模态分解、样本熵和Markov 链，提出一种中长期风速仿真方法，进而仿真某风电场某月的风速样本。结果表明，仿真风速样本能较好地集成实测风速样本的时序性和概率特性。

现有文献从多个角度建立了风速仿真模型，能较好地处理风速仿真问题，但仍难以仿真任意时间步长的风速样本，且仿真风速样本的时间步长常受限于实测风速样本的时间步长。例如，基于小时级实测风速样本的风速仿真模型通常仅能产生小时级仿 真 风 速 样 本。 为 此，文 献［13］将Ornstein-Uhlenbeck（下文简称OU）过程引入风速仿真模型中，可产生任意时间步长的仿真风速样本，但OU 过程服从正态分布，且可能产生数值为负的仿真风速样本，与实测风速样本的物理属性相悖。

因此，本文提出基于互转换OU 过程的风速仿真模型，应用风速概率分布和正态分布将实测风速样本转换为风速高斯随机过程样本，进而便于OU过程对其建模和替代，随后将OU 过程的仿真样本逆转换为仿真风速样本。本文将此OU 过程的转换-逆转换流程称为互转换OU 过程，该过程可确保仿真风速样本服从合适的参数型风速概率分布，消除取值为负的仿真风速样本，且OU 过程可为仿真风速样本设定任意时间步长，进而克服文献［13］的不足。

此外，将本文基于互转换OU 过程的风速仿真模型与时序Monte Carlo 模拟法结合，提出仿真时间步长可变的含风能发电系统充裕度评估方法，研究不同仿真时间步长和风况对含风能发电系统充裕度评估精度和结果的影响，进而展示本文风速仿真模型的应用性和实用性。

1 基于互转换OU 过程的风速仿真模型

由于OU 过程服从正态分布［14］，难以直接用于风速随机过程建模，故本文提出基于互转换OU 过程的风速仿真模型，总体建模思路如图1 所示。

图1 基于互转换OU 过程的风速仿真建模Fig.1 Wind speed simulation modeling based on mutual conversion based OU process

1.1 风速高斯随机过程

记vt为风速随机过程样本，则可应用风速累积分布函数将vt转换为过渡随机过程样本rt，即

式中：F(·)为风速累积分布函数；rt服从［0，1］均匀分布。

进一步，应用标准正态逆累积分布函数将过渡随机过程样本rt转换为风速高斯随机过程样本zt，即

式中：Φ-1(·)为标准正态逆累积分布函数。

1.2 应用OU 过程表示风速高斯随机过程

OU 过程是描述高斯随机过程的常用模型之一，且OU 过程具有均值回复特性，本文应用OU 过程替代表示风速高斯随机过程，则OU 过程可表示为以下随机微分方程［14］。

上式表明，若以OU 过程替代表示风速高斯随机过程，会改变风速高斯随机过程的分布参数，由标准正态分布变换为均值和方差分别为μz和σ2z/2τz的正态分布。

上式表明，随着相距时段的增大，t1和t2时刻间的OU 过程相关性呈现指数衰减趋势，这与不同时刻风速间相距时段越长，相关性递减的物理现象类似。

记v1，v2，…，vN为收集到的N组实测风速样本，相邻实测风速样本间的时间步长为Δt，该时间步长由实测风速样本的来源数据库决定，可为1 min、1 h等。将实测风速样本代入式（1），可得N组过渡随机 过 程 样 本r1，r2，…，rN。而 后 再 将r1，r2，…，rN代入式（2），可得N组风速高斯随机过程样本z1，z2，…，zN。记OU 过程的仿真时间步长为Δs，则可根据z1，z2，…，zN和最大似然估计法［16］，得到式（3）中OU 过程的参数μz、τz和σz，详细参数估计公式如下［16］。

其中，参数Zx、Zy、Zxx、Zxy和Zyy分别为［16］：

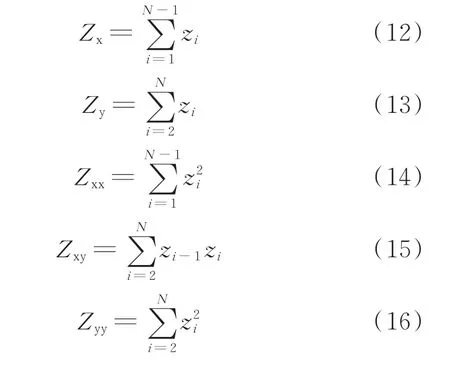
值得注意的是，OU 过程的仿真时间步长Δs可小于Δt，即OU 过程可产生比实测风速样本时间步长更短的OU 过程仿真样本。

1.3 基于互转换OU 过程的风速仿真算法

在1.2 节从实测风速样本转换和估计得到OU过程参数的基础上，采用文献［17］的方法，从OU 过程中抽样时间步长为Δs的任意组OU 过程仿真样本，用以替代风速高斯随机过程仿真样本。然后，对这些样本进行逆转换，则可得到时间步长为Δs的任意组仿真风速样本，所以，本文中变量Δs同时表示OU 过程仿真样本的时间步长和仿真风速样本的时间步长。将该风速仿真过程总结为基于互转换OU过程的风速仿真算法，详细步骤如下。

步骤1：确定待产生的仿真风速样本数量M和仿真风速时间步长Δs。

步骤2：应用式（1）—式（16）将N组实测风速样本转换为N组风速高斯随机过程样本，并从中估计OU 过程参数，进而使用OU 过程替代表示风速高斯随机过程。

步骤3：抽样产生M组时间步长为Δs的标准正态分布随机数nΔs，n2Δs，…，nMΔs，将其代入式（17），得到M组时间步长为Δs的Wiener 过程增量仿真样本ΔWΔs，ΔW2Δs，…，ΔWMΔs［17］，即

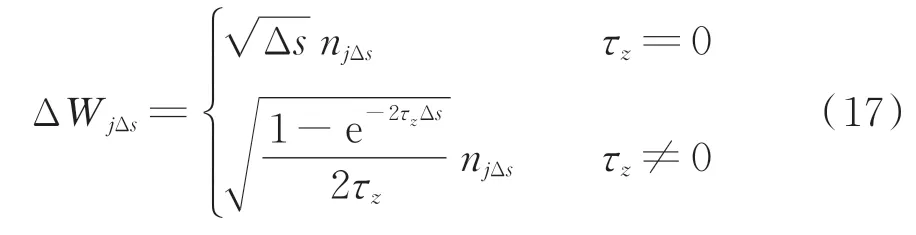
式 中：njΔs和ΔWjΔs分 别 为 时 刻jΔs(j=1，2，…，M)的标准正态分布随机数和Wiener 过程增量仿真样本。

2 仿真时间步长可变的含风能发电系统充裕度评估方法

在应用发电系统充裕度评估的时序Monte Carlo 模拟法前，需设定仿真时间步长，并假设单位仿真时间步长内系统可用容量和负荷需求维持恒定［18］，仿真时间步长的取值会影响充裕度评估精度和结果，也能凸显风能的短期波动性。

2.1 仿真时间步长对充裕度评估结果的影响

图2（a）和（b）所示分别为仿真时间步长取值Δs和0.5Δs下时刻jΔs至时刻（j+2）Δs间含风能发电系统可用容量和系统负荷需求仿真曲线的两组典型场景，图中阴影部分为失电量βENS。在图2（a）中，可用容量始终高于负荷需求，所以失电持续时间βLLD、失电频次βLLO和失电量βENS均为0。假设仿真时间步长缩短为0.5Δs后，可用容量的均值不变并在较短时间步长内围绕均值波动，则由图2（b）中看到，失电 持 续 时 间βLLD和 失 电 频 次βLLO分 别 增 至Δs和2 次，失电量βENS大于0。

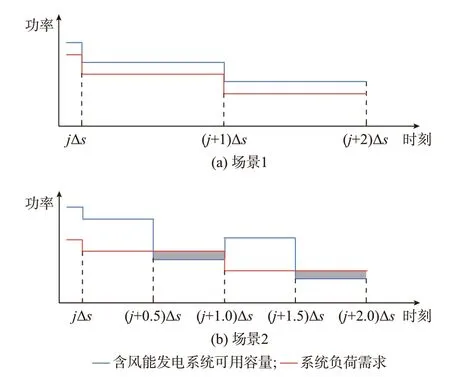
图2 可用容量高于负荷需求时含风能发电系统充裕度评估的两组典型场景Fig.2 Two typical scenarios of adequacy assessment of wind-integrated generation system when available capacity is higher than load demand

图3（a）和（b）所示分别为仿真时间步长取值Δs和0.5Δs下时刻jΔs至（j+2）Δs间含风能发电系统可用容量和系统负荷需求仿真曲线的另外两组典型场景。在图3（a）中，可用容量始终低于负荷需求，所以失电持续时间βLLD和失电频次βLLO分别为2Δs和0 次，失电量βENS大于0。图3（b）中，可用容量在更短时间步长内围绕均值波动，使得失电持续时间βLLD降 至Δs，失 电 频 次βLLO增 至2 次，失 电 量βENS大于0。

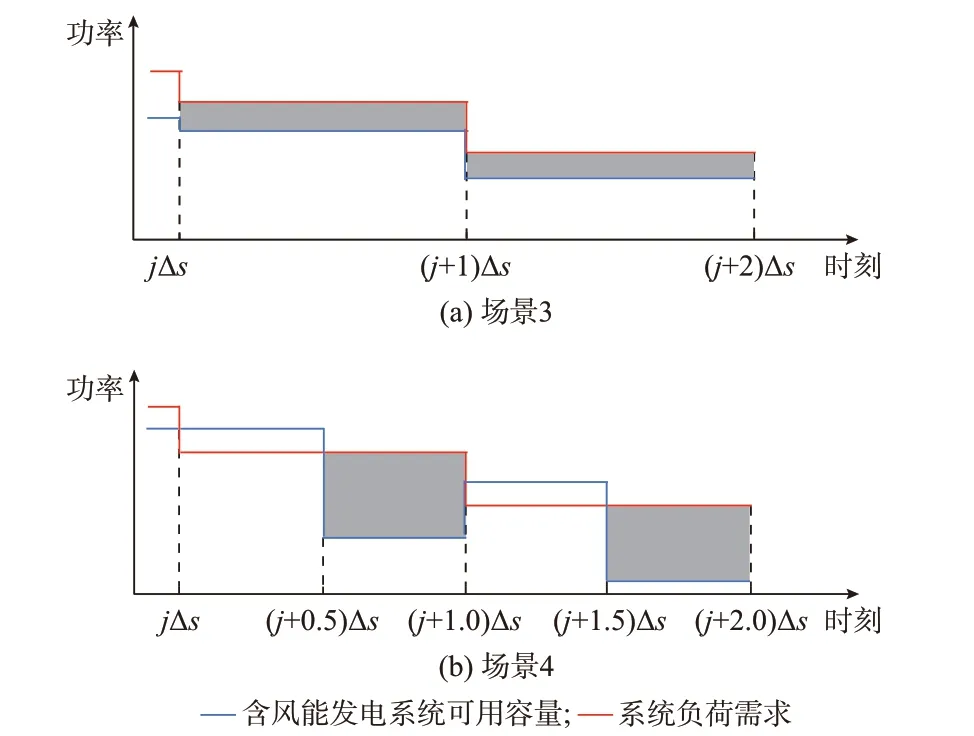
图3 可用容量低于负荷需求时含风能发电系统充裕度评估的两组典型场景Fig.3 Two typical scenarios of adequacy assessment of wind-integrated generation system when available capacity is lower than load demand

综上，在图2 和图3 的场景下，失电频次βLLO会随着仿真时间步长的减小而增大，而失电持续时间βLLD和失电量βENS则随着仿真时间步长的减小而改变。所以，期望失电频率γLOLF会随着仿真时间步长的减小而增大，期望失电持续时间γLOLE和期望失电量γLOEE会随着仿真时间步长的减小而改变。

2.2 充裕度评估步骤

当发电系统中风电渗透率较高时，由于风速不确定性，可能导致较短时间内系统可用容量发生波动，因此，需在充裕度评估中设定较短仿真时间步长，以便充分评估风速不确定性对系统充裕度的影响。本文提出的基于互转换OU 过程的风速仿真模型能应对该挑战，为含风能发电系统充裕度评估提供任意仿真时间步长下的任意组仿真风速样本。为此，本文将基于互转换OU 过程的风速仿真模型与时序Monte Carlo 模拟法结合，提出仿真时间步长可变的含风能发电系统充裕度评估方法，详细步骤如下：

步骤1：初始时刻，假设所有发电机组（常规机组和风电机组）均处于正常运行状态，并根据充裕度评估精度设定仿真风速样本的时间步长Δs。

步骤2：抽样所有发电机组的状态持续时间步长数。

1）如果第k台发电机组处于运行状态，则该机组处于运行状态的时间步长数θk，Δs可由式（21）抽样确定。

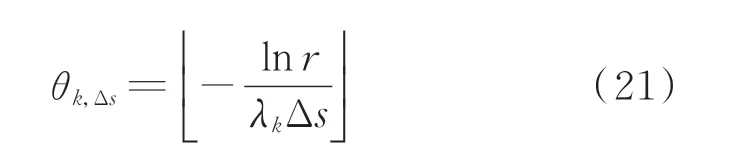
式中：λk为第k台发电机组的故障率；r为［0，1］区间均匀分布的随机数表示对数据进行向下取整的运算。

2）如果第k台发电机组处于停运状态，则该机组处于停运状态的时间步长数ηk，Δs可由式（22）抽样确定。

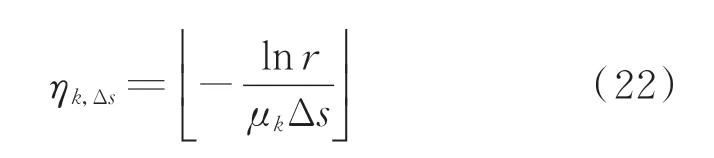
式中：μk为第k台发电机组的修复率。

步骤3：基于1.3 节步骤1 至步骤6，产生时间步长为Δs的仿真风速样本。

步骤4：根据常规发电机组的运行状态，计算所有常规发电机组的可用容量PG。

式中：Gk为第k台处于运行状态的常规发电机组的额定容量；NG为处于运行状态的常规发电机组数量。

步骤5：根据风电机组的运行状态、仿真风速样本和风电转换函数，计算风电场的可用容量PWF。

式中：NWF为处于运行状态的风电机组的数量；Pg(·)为第g台处于运行状态的风电机组的风电转换函数［19］，具体如式（25）所示。

式中：v为瞬时风速；vci、vr、vco和Pr分别为第g台风电机组的切入、额定、切出风速和额定容量；系数A、B和C可由vci和vr计算得到，详细计算公式可参见文献［20］。

步骤6：根据PG、PWF和系统年负荷，计算第q组仿真年度内的失电持续时间βLLD，q、失电频次βLLO，q和失电量βENS，q。

步骤7：当仿真至Q年度后，计算系统充裕度指标（γLOLE、γLOLF、γLOEE），计算公式如下［18］。

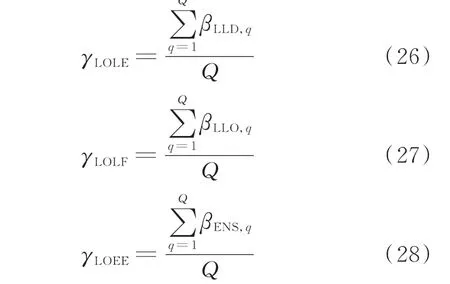
步骤8：重复步骤2 至步骤7，直到γLOEE的方差系数低于0.02 或Q大于最大仿真年数，则停止仿真，输出充裕度指标γLOLE、γLOLF和γLOEE。

3 算例分析

本章将应用实测风速样本验证本文基于互转换OU 过程的风速仿真模型，评估含风能IEEE-RTS发电系统充裕度，分析不同仿真时间步长和不同风况对充裕度评估精度和结果的影响。

3.1 基于互转换OU 过程的风速仿真模型验证

通过访问开放气象数据库北达科他州农业气象网 络（North Dakota agricultural weather network，NDAWN），收集Bottineau 观测站2011 年至2020 年间每小时的实测风速样本［21］，故实测风速样本的时间步长Δt为1 h。应用文献［22］提供的风速Weibull分布等9 类参数型非混合分布和最大似然估计法拟合Bottineau 观测站的风速概率分布，并根据赤池信息准则选取拟合优度最高的参数型概率分布。图4所示为Bottineau 观测站的实测风速样本频率直方图、风速Weibull、风速广义极值（generalized extreme value，GEV）和风速Gamma（用GA 表示）概率密度曲线。AWeibull、AGEV和AGA分别表示3 类参数分布的赤池信息，可得AWeibull=523 178，AGEV=526 241，AGA=523 248。可以看出，AWeibull最低，表明从赤池信息的角度，风速Weibull 分布的拟合优度高于另外两类分布。在图4 中，虽然风速GA 概率密度曲线较风速Weibull 概率密度曲线更贴近实测风速样本频率直方图的峰值区域，但风速Weibull 概率密度曲线较风速GA 概率密度曲线更贴近5 mph（1 mph=1.6 km/h）至20 mph 间的实测风速样本频率直方图。总体上，风速Weibull 分布能较高精度地拟合Bottineau 观测站的风速概率分布，故采用风速Weibull 分布表示Bottineau 观测站的风速概率分布。Bottineau 观测站的实测风速样本均值、标准差、偏度和峰度分别为8.66 mph、5.37 mph、0.93 和3.79，其风速Weibull 尺度和形状参数分别为9.723 2和1.679 8。

图4 Bottineau 观测站的实测风速样本频率直方图、风速Weibull、风速GEV 和风速GA 概率密度曲线Fig.4 Histogram of measured wind speed frequency,probability density curves of Weibull, GEV, GA for wind speed at Bottineau observatory

应用1.1 节方法将Bottineau 观测站的实测风速样本转换为风速高斯随机过程样本，而后设定仿真时间步长Δs分别为1、0.5、0.25、0.125 h，应用式（7）—式（16）估计互转换OU 过程的参数，对应取值见附录A 表A1。可以看到，互转换OU 过程的均值和方差不随仿真时间步长的改变而改变，且与标准正态分布的均值和方差相差较小，表明互转换OU 过程的概率分布特征与风速高斯随机过程的概率分布特征相似。另一方面，互转换OU 过程的均值回复速度和瞬时波动参数随着仿真时间步长的减小而增大。

设 定 仿 真 时 间 步 长Δs分 别 为1、0.5、0.25、0.125 h，应用1.3 节步骤1 至6 产生1 年8 760 h 的仿真风速样本。作为对比，应用基于传统OU 过程的风速仿真模型产生相同时段的仿真风速样本，该仿真风速样本的抽样步骤与1.3 节步骤1 至6 类似，但不使用步骤2 中实测风速样本的转换和步骤6 中仿真风速样本的逆转换操作。假设在单位时间步长内风速恒定，则可得出其中第1 585 h 至1 633 h 间的48 h 本文仿真风速曲线、基于传统OU 过程仿真风速曲线和实测风速曲线，如附录A 图A1（a）至（d）所示。可以看到，在图A1（a）中基于传统OU 过程仿真风速曲线在两处时段内取值为负，与实测风速样本的物理属性相悖，而本文仿真风速曲线始终保持为非负值，与实测风速样本的物理属性一致，在图A1（b）至（d）中也能观察到类似现象。同时，随着仿真时间步长的缩短，本文仿真风速曲线逐渐接近于连续变化的风速曲线，更能凸显风速短期随机波动性，当仿真时间步长设定足够小时，本文仿真风速曲线可近似替代连续变化的风速曲线。另一方面，本文仿真风速曲线不是预测风速曲线，故本文仿真风速曲线与实测风速曲线在相同时段内存在较大差异。类似地，也可得到其他时段的仿真风速曲线和实测风速曲线，但限于篇幅，故不在文中展示。

附录A 图A2（a）和（b）所示分别为不同仿真时间步长下，本文仿真风速样本、基于传统OU 过程仿真风速样本和实测风速样本在滞后10 h 内的自相关系数曲线。其中，自相关系数曲线上相邻散点间的横向距离代表该风速样本的时间步长。可以得出以下结论。

1）当时间步长同为1 h 且滞后时段为0 至2 h之间时，本文仿真风速样本和基于传统OU 过程仿真风速样本的自相关系数曲线均接近实测风速样本的自相关系数曲线，但随着滞后时段增加，两类仿真风速样本的自相关系数曲线均偏离实测风速样本的自相关系数曲线，前者的偏离程度小于后者的偏离程度。

2）由于均值回复速度参数τz和τ*z随着仿真时间步长的减小而增大，使得式（6）中不同时刻间OU过程协方差的指数项减小，进而使得两类仿真风速样本的自相关系数曲线随着仿真时间步长的减小向下移动。

以上现象表明，可通过改变时间步长，调整仿真风速样本自相关系数曲线的上下位置。例如，当时间步长同为1 h 时，基于传统OU 过程仿真风速样本的自相关系数曲线在大部分滞后时段高于实测风速样本的自相关系数曲线，如将时间步长减小为0.5 h，则基于传统OU 过程仿真风速样本的自相关系数曲线向下移动，更贴近时间步长为1 h 下实测风速样本的自相关系数曲线。值得注意的是，当时间步长同为1 h 时，本文仿真风速样本的自相关系数曲线已较贴近实测风速样本的自相关系数曲线，无须再改变时间步长。

附录A 图A3（a）至（d）所示分别为不同仿真时间步长下，基于传统OU 过程仿真风速样本频率直方图和Bottineau 观测站的风速Weibull 概率密度曲线。可以看到，基于传统OU 过程仿真风速样本频率直方图与风速Weibull 概率密度曲线的契合度较低，部分频率直方图出现在负半轴上，表明基于传统OU 过程仿真风速样本未能保留风速Weibull 分布特征。

附录A 图A4（a）至（d）所示分别为不同仿真时间步长下，本文仿真风速样本频率直方图和Bottineau 观测站的风速Weibull 概率密度曲线。可以看到，尽管仿真时间步长不同，本文仿真风速样本频率直方图始终与风速Weibull 概率密度曲线保持较高程度的契合，表明本文仿真风速样本能较高精度地保持风速Weibull 分布特征。

表1 所示为不同仿真时间步长下，本文仿真风速样本和基于传统OU 过程仿真风速样本的均值、标准差、偏度和峰度。与实测风速样本的均值、标准差、偏度和峰度对比可以看到，基于传统OU 过程仿真风速样本的偏度和峰度与实测风速样本的偏度和峰度相差较大。尽管仿真时间步长不同，本文仿真风速样本的均值、标准差、偏度和峰度仍与实测风速样本的均值、标准差、偏度和峰度相差较小。

表1 不同仿真时间步长下，Bottineau 观测站仿真风速样本的均值、标准差、偏度和峰度Table 1 Mean value, standard deviation, skewness,and kurtosis of simulated wind speeds from Bottineau observatory with different simulation time steps

至此，通过以上分析，表明本文基于互转换OU过程的风速仿真模型能产生任意时间步长下的仿真风速样本，且仿真风速样本具备与实测风速样本类似的概率分布特征和统计指标，仿真风速样本的自相关系数随着滞后时段的增大而减小，也与实测风速样本的自相关系数递减的规律类似。同时，本文仿真风速样本可克服基于传统OU 过程仿真风速样本中含负值仿真风速样本和概率分布特征与实测风速样本概率分布特征契合度较低的不足，进而验证本文风速仿真模型的准确性和有效性。

3.2 含风能IEEE-RTS 发电系统的变仿真时间步长充裕度评估

原始IEEE-RTS 发电系统含有总装机容量为3 405 MW 的32 台常规发电机组，系统峰值负荷为2 850 MW，详细的机组和负荷数据可参见文献［18］。文献［18］中设定仿真时间步长为1 h，评估原始IEEE-RTS 发电系统的充裕度指标γLOLE、γLOEE和γLOLF分 别 为9.371 6 h/a、1 197.444 8 MW·h/a 和1.919 2 次/a。

假设在Bottineau 观测站建设由300 台相同型号风电机组组成的风电场，风电机组的切入、额定、切出风速、额定功率和轮毂高度分别为3 m/s、10 m/s、25 m/s、2 MW 和100 m，风电机组故障率和修复时间分别为2 次/a 和480 h/次，所以Bottineau 风电场的总装机容量为600 MW。

假设Bottineau 风电场接入原始IEEE-RTS 发电系统，应用2.2 节步骤1 至8 评估仿真时间步长分别为1、0.5、0.25、0.125 h 下的含风能IEEE-RTS 发电系统充裕度指标。作为对比，分别使用基于传统OU 过程的风速仿真模型和实测风速样本，评估不同仿真时间步长下的含风能IEEE-RTS 发电系统充裕度指标，结果如表2 所示。其中，括号内的百分数为当前仿真时间步长下充裕度指标相对于前一仿真时间步长下充裕度指标的变化百分比。值得注意的是，根据式（25），取值为负的仿真风速样本不会使风电机组产生功率输出。此外，由于Bottineau 观测站的风速测量高度为3 m，因此本文应用插值方法将仿真风速转换至100 m 风电机组轮毂高度处的仿真风速，详细转换公式可参见文献［23］。对比原始IEEE-RTS 发电系统充裕度指标和表2，可以得到以下结论：

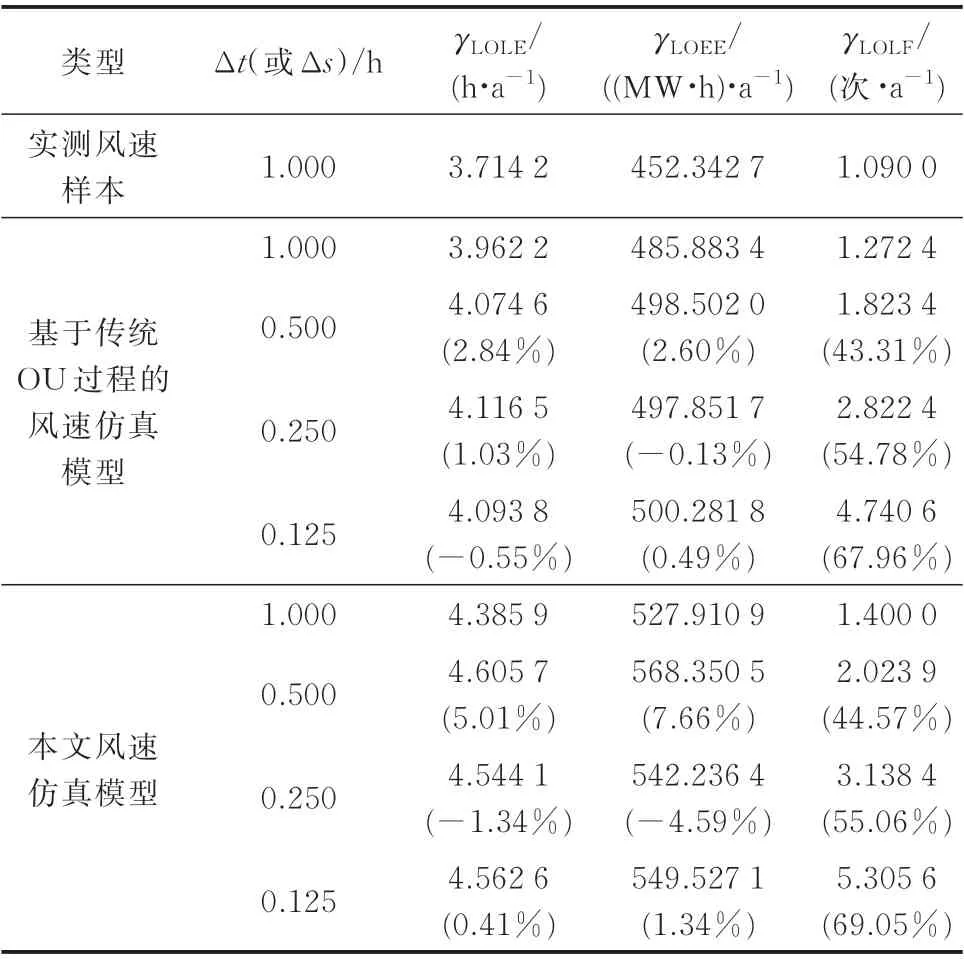
表2 不同仿真时间步长下，含风能IEEE-RTS 发电系统充裕度指标Table 2 Adequacy indices of wind-integrated IEEERTS generation system with different simulation time steps

1）当仿真时间步长为1 h 时，风电场接入后，γLOLE、γLOEE和γLOLF指标均减小，表明风电场并网具有一定的充裕度效益。

2）当仿真时间步长为1 h 时，基于本文风速仿真模型和基于传统OU 过程的风速仿真模型评估所得的γLOLE、γLOEE和γLOLF指标均高于基于实测风速样本评估所得的γLOLE、γLOEE和γLOLF指标。

3）随着仿真时间步长的减小，基于本文风速仿真模型和基于传统OU 过程的风速仿真模型评估所得的γLOLF指标均以43.31%～69.05% 的比例大幅增大。

4）随着仿真时间步长的减小，基于本文风速仿真模型和基于传统OU 过程的风速仿真模型评估所得的γLOLE和γLOEE指标以-4.59%～7.66%的比例小幅波动。

以上现象表明，基于实测风速样本的充裕度评估结果与基于仿真风速样本的充裕度评估结果间具有一定差距，该差距可能源于仿真风速样本未能完全保持实测风速样本的概率分布特征和自相关系数曲线。在充裕度评估中设定较大的仿真时间步长，将导致对γLOLF指标较大程度低估，但对γLOLE和γLOEE指标的错估程度较小。另一方面，γLOLF指标对仿真时间步长的敏感度高于γLOLE和γLOEE指标对仿真时间步长的敏感度。可根据该敏感度关系，为含风能发电系统充裕度评估选定精度和复杂度折中的仿真时间步长。

3.3 不同风况对充裕度评估结果的影响

为评估不同风况对充裕度评估结果的影响，从NDAWN 收 集Crosby 和Linton 观 测 站2011 年 至2020 年间每小时的实测风速样本［21］，应用文献［22］的方法拟合两座观测站的风速概率分布，发现GEV分布和GA 分布分别能以最小的赤池信息拟合两座观测站的风速概率分布，所以，选择GEV 分布和GA 分布分别表示两座观测站的风速概率分布。

附录A 图A5 和图A6 所示分别为Crosby 和Linton 观测站的实测风速样本频率直方图、风速Weibull、风速GEV、风速GA 概率密度曲线和3 类参数分布的赤池信息。可以看到，在附录A 图A5中，AGEV最低，且风速GEV 概率密度曲线较另外两类概率密度曲线更贴近实测风速样本频率直方图的峰值和尾部区域，表明在Crosby 观测站，风速GEV分布的拟合优度高于另外两类分布的拟合优度。在附录A 图A6 中也能看到类似现象，即AGA最低，风速GA 概率密度曲线较另外两类概率密度曲线更贴近实测风速样本频率直方图的峰值和尾部区域，表明在Linton 观测站，风速GA 分布的拟合优度高于另外两类分布的拟合优度。

以上现象表明，不同观测站的风况各异，风速Weibull 分布难以适用于所有观测站，应根据拟合优度从多类候选参数型分布中优选最合适的参数型分布，用以表示特定观测站的风速概率分布。另一方面，通过将式（1）和式（20）中的风速累积分布函数及其逆函数替换为拟合优度最高的风速GEV 分布和风速GA 分布的累积分布函数及其逆函数，则本文风速仿真模型可为Crosby 和Linton 观测站提供服从风速GEV 分布和GA 分布的仿真风速样本，体现本文风速仿真模型在处理风速概率分布多样性问题上的灵活性。应用本文风速仿真模型和基于传统OU 过程的风速仿真模型产生不同仿真时间步长下Crosby 和Linton 观测站8 760 h 内的仿真风速样本，并计算仿真风速样本与实测风速样本的均值、标准差、偏度和峰度，结果如附录A 表A3 所示。可以看到，尽管观测站不同，相较基于传统OU 过程仿真风速样本，本文仿真风速样本的均值、标准差、偏度和峰度仍与实测风速样本的均值、标准差、偏度和峰度更接近。这表明本文风速仿真模型可较为准确地计及不同观测站的风速概率分布特征。另外，从Bottineau 观测站实测风速样本的统计指标和表A3看到，Linton 观测站的风速均值最高，表明该观测站风能资源最充沛。

假设Crosby 和Linton 观测站分别建有由300 台相同型号风电机组组成的风电场，两观测站的风速分别服从风速GEV 分布和风速GA 分布，风电机组的参数与3.2 节的风电机组参数相同，且两处风电场分别接入原始IEEE-RTS 发电系统，应用2.2 节步骤1 至8 评估不同仿真时间步长下的含风能IEEE-RTS 发电系统充裕度指标。类似地，作为对比，分别使用基于传统OU 过程的风速仿真模型和实测风速样本，评估不同仿真时间步长下的含风能IEEE-RTS 发电系统充裕度指标。结果如附录A 表A4 所示，其中，观测站名称旁括号内的GEV 和GA分别表示对应观测站的风速概率分布类型。对比表2 和附录A 表A4 可以得到以下结论。

1）Linton 风 电 场 接 入IEEE-RTS 发 电 系 统 后，在相同仿真时间步长下，系统的γLOLE、γLOEE和γLOLF指标均低于另外两座风电场接入后系统的γLOLE、γLOEE和γLOLF指标。

2）尽管风况不同，随着仿真时间步长的减小，γLOLF指标仍以46.62%～77.55%的比例大幅增大。

3）尽管风况不同，随着仿真时间步长的减小，γLOLE和γLOEE指标仍保持-3.69%～5.20%的比例小幅波动。

4）尽管风况不同，当仿真时间步长为1 h 时，基于仿真风速样本评估所得的γLOLE、γLOEE和γLOLF指标均高于基于实测风速样本评估所得的γLOLE、γLOEE和γLOLF指标。

以上现象表明，风能资源越充沛，则风电场并网的充裕度效益越显著。另一方面，尽管风况不同，若在充裕度评估中设定较大仿真时间步长，仍会造成γLOLF指标被较大程度低估，但对γLOLE和γLOEE指标的错估程度较小。另一方面，即使风况不同，γLOLF指标对仿真时间步长高敏感和γLOLE、γLOEE指标对仿真时间步长低敏感的现象依然存在。为准确评估γLOLF指标，应选取较小的仿真时间步长。另外，即使风况不同，由于仿真风速样本未能完全保留实测风速样本的不确定性特征，仍会造成充裕度评估结果存在一定差距。

在附录A 表A4 算例的基础上，应用风速Weibull 分布替换Crosby 和Linton 观测站的风速GEV 分布和风速GA 分布，再应用2.2 节步骤1 至8评估不同仿真时间步长下含风能IEEE-RTS 发电系统充裕度指标，结果如表A5 所示。表A5 中充裕度指标随仿真时间步长减小后的变化趋势与表A4 中相应指标的变化趋势类似，采用拟合优度欠佳的风速Weibull 分布会导致充裕度指标的小幅误差。

4 结语

本文提出基于互转换OU 过程的风速仿真模型，可产生任意时间步长的仿真风速样本，且仿真风速样本具有与实测风速样本类似的概率分布特征和自相关特征。同时，将本文风速仿真模型与时序Monte Carlo 模拟法结合，提出仿真时间步长可变的含风能发电系统充裕度评估方法，可评估任意仿真时间步长下的含风能发电系统充裕度指标。

应用Bottineau 观测站多年实测风速样本验证本文风速仿真模型，并评估不同仿真时间步长和风况下含风能IEEE-RTS 发电系统充裕度指标，得出以下结论。

1）本文风速仿真模型能产生与实测风速样本概率分布特征和自相关特征类似的任意时间步长下的仿真风速样本，克服基于传统OU 过程的风速仿真模型产生负值仿真风速样本和概率分布特征契合度欠佳的不足。

2）风电场并网将对发电系统产生充裕度效益，不同风况将影响风电场并网的充裕度效益，该充裕度效益与风能资源充沛程度正相关。

3）γLOLF指标对仿真时间步长的敏感度高于γLOLE、γLOEE指标对仿真时间步长的敏感度，在充裕度评估中设定较大的仿真时间步长，将导致对γLOLF指标的低估程度较大和对γLOLE、γLOEE指标的错估程度较小。

本文下一步的研究方向拟将Markov 链与互转换OU 过程结合，进而更准确地仿真风速在不同风级或风速尺度间的随机转移关系。此外，也可将相关系数矩阵法与互转换OU 过程结合，进而计及多个风电场风速的互相关性。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。