基于逆变型电源暂态电流回代的系统级故障暂态解析

贾 科，杨 彬，刘 浅，郑黎明，毕天姝

（新能源电力系统国家重点实验室（华北电力大学），北京市 102206）

0 引言

在中国电力系统高比例电力电子设备和新能源接入的发展趋势下［1-2］，系统短路电流呈现幅值受限且低次谐波含量丰富等特征，导致传统工频量保护动作性能下降，基于故障全时域量的保护将成为未来 保 护 发 展 趋 势 之 一［3-6］。 对 含 逆 变 型 电 源（inverter interfaced generator，IIG）的电力系统故障暂态特征的精准刻画是全时域量保护的研究基础。

国内外有关IIG 单机故障暂态解析的研究经历了仿真分析、频域传递函数解析和时域方程解析3 个阶段。早期研究基于故障仿真对IIG 的故障暂态过程和主导因素展开了定性分析［7-9］，但该类研究依赖于电磁仿真，无法从机理层面揭示IIG 故障暂态规律；频域传递函数解析［10-13］以输出电流与端电压、电流指令值间的频域传递函数展开分析，但由于多机互联系统的频域模型难以求解，单机暂态电流解析结论并不适于推广至多机系统分析。时域方程解析对IIG 不同故障控制下的暂态电流分别进行了解析分析。文献［5，14-15］通过建立关于输出电流的二阶微分方程推导了低电压穿越（low voltage ride through，LVRT）控制下机组故障暂态电流的时域解；文献［16-17］通过计算直流电压动态，进而对故障后仍处于常规控制下的机组暂态输出实现了解析分析。采用上述方法，针对单机-无穷大系统中IIG的暂态电流已得到了较为完备的解析结论。但不同于单机解析，多机系统故障暂态解析需考虑不同时间尺度下机组间的交互作用［18］和各机组输出电流的相位换算［19］。现有多机系统故障分析研究仅停留于稳态分析［19-20］，尚未见暂态解析研究，这将使全时域量保护发展受碍于无法整定。

多机系统故障暂态解析主要面临2 个挑战：一是IIG 输出电流均以机端电压为相位参考调制得到，IIG 单机解析所得暂态电流并非实际多机并网系统中各机组的输出值，因此需计及端电压相位动态，对机组暂态电流进行向统一参考系下的动态相位换算；二是多IIG 接入网络构成多输入多输出系统（multiple-input multiple-output，MIMO）［21］，其动态方程呈高阶非线性，难以求解。

本文针对高比例并网型IIG 接入系统的对称故障，提出一种基于动态相位换算与系统方程暂态修正的系统级故障电流全时域解析方法。以IIG 单机故障暂态解析为基础，根据功角关系对不同故障控制策略下IIG 的暂态输出实现动态相位换算；通过对系统方程进行暂态修正，避免多机系统动态方程的高阶运算；在此基础上，IIG 暂态电流可进行直接回代，从而得到故障点及全网暂态电流的全时域精确解。采用PSCAD/EMTDC 搭建IEEE 33 节点仿真系统，验证了所提方法的有效性，可为高比例电力电子设备和新能源接入电力系统的全时域量保护研究提供参考。

1 新能源接入电力系统故障暂态解析方法

1.1 不同故障控制策略下IIG 单机暂态解析

对于新能源多机接入的电力系统，故障后不同空间分布的机组所感知到的机端电压降落程度不同，系统内势必将出现常规控制机组（远故障处）与LVRT 控制机组（近故障处）共存的情况。对不同故障控制策略下的IIG 单机暂态电流的解析是多机系统暂态解析的基础。

本节以经典双闭环控制结构的IIG 为例进行介绍，其常见的一次回路拓扑和双闭环控制主回路如图1 所示。

图1 IIG 一次回路与控制回路示意图Fig.1 Schematic diagram of primary circuit and control loop of IIG

图1 中，PWM 表示脉宽调制；PI 表示比例-积分环节；udc为直流电压；id、iq分别为交流电流d、q轴分量；ud、uq分别为公共连接点（PCC）处电压d、q轴分量；上角标“*”表示相应的指令值；ω为电气角频率；Lf为滤波器电感；e*d、e*q分别为电流内环输出电压d、q轴分量指令值。当故障后端电压高于0.9 p.u.时，IIG 仍保持常规控制，直流电压外环与电流内环均作用，其故障暂态输出由直流电容动态和电压外环主导。基于逆变器交直流侧功率关系，即可求解故障后直流电压暂态量如式（1）所示，代入内环控制方程即可得到交流侧故障电流d轴分量的暂态解析式（2）（常规控制下IIG 运行在单位功率因数状态，q轴电流被控制为0）：

式中：Δudc为直流电压故障分量；Uf为机端电压故障后幅值；udc0直流电压故障前初始值；Pout0为故障前IIG 输出有功功率初始值；kup、kui分别为电压外环PI控制器的比例、积分系数；K、K1、K2、μ1、μ2、λ1和λ2分别为与IIG 控制参数、初始运行状态相关的各项系数，具体推导详见文献［16］，其中K与Pout、Uf、udc0、C相关，K1和K2与kup、kui、K相关；C为直流电容。

对于机组端电压降落严重的IIG，故障后进入LVRT 控制，其故障暂态输出由端电压和内环控制决定。通过联立内环控制与外电路方程得到关于输出电流id、iq的二阶微分方程，从而解得LVRT 控制下IIG 的暂态电流解析式：

式中：UN、IN分别为IIG 正常运行时PCC 处的稳态电压、电流幅值。

借助系统故障稳态计算方法［19］可求解各机组接入节点电压故障后稳态幅值Uf，从而依据式（2）至式（5）得到多机互联系统内各IIG 单机暂态电流。

但上述单机解析方法均以IIG 机端电压为参考相位求得暂态输出电流id、iq。在实际多机互联系统中由于各机组输出的相位参考（即机端电压）互不相同，因此，IIG 单机暂态解析结论无法直接应用于多机系统的故障暂态电流计算，需将各IIG 暂态电流换算至统一参考坐标系下分析。如图2（a）所示，任一并网IIG 输出电流I∠θI均以其机端电压U∠θU为相位参考，而在进行系统计算时又往往需在统一相位参考（通常为无穷大系统电势E∠0°）下对所有电气量进行计算。因此，在进行系统级暂态计算时须计及电压之间相对相位的动态变化过程。另外，暂态期间节点电压相位也存在暂态过渡过程，与电流动态叠加后，将导致IIG 实际输出电流不同于单机解析结论，如图2（b）、（c）所示。因此，在进行系统级暂态分析时需要对单机暂态解析电流进行统一参考系下的动态相位换算。

图2 单机与多机系统中IIG 输出电流Fig.2 Output currents of IIG in single-generator and multi-generator systems

1.2 面向暂态解析的IIG 电流动态相位换算

首先，定义IIG 单机暂态电流id、iq为局部量，将换算至统一参考系（以电势E为该参考系d轴方向）下的电流iD、iQ定义为全局量。局部量与全局量实质为同一电流，但二者之间存在因观测参考系不同而产生的相角差（等于机端电压Upcc与E之间的相位差），在系统级分析时需计及相位换算：

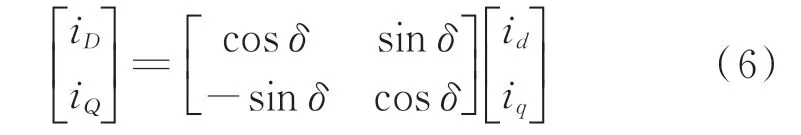
式中：δ为两参考系间的动态相角差。多机故障稳态计算将相位换算计入IIG 的数学模型［19］，可依赖迭代优化和收敛判据对其处理。但对于故障暂态分析而言，动态期间网络各节点电压相位受机组输出动态决定，难以解析。

依据交流网络功角关系可知，IIG 机端电压相位过渡过程取决于暂态期间其有功功率的动态。分析故障发生至故障稳态过程，IIG 机组输出功率从Pout0变化为Poutf。对于故障后机组进入LVRT 控制的情况，由于内环响应较快，可近似认为故障后相位呈阶跃变化；而对于故障后机组仍处于常规控制下的情况，IIG 输出主要受直流电压外环影响，其动态过程需进一步讨论。

忽略逆变器功耗，可得故障暂态期间IIG 输出有功功率Pout为：

式中：Pin为逆变电源直流侧输入功率，故障期间可认为恒定不变；r1、r2为指数项的衰减系数。

依据逆变器参数整定原则［16］，通常有r2＞10r1。因此，式（7）可以进一步简化为：

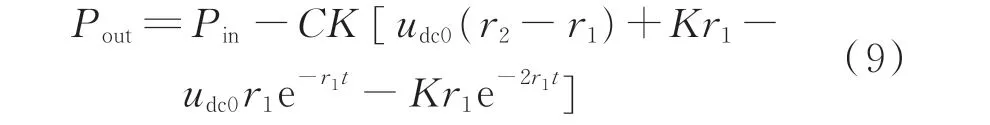
对于故障后仍处于常规控制下的IIG，由于其距故障点较远，故障前后机端电压幅值及相位变化不大。因此，故障暂态期间相位增量可进行线性化，则可得机组出口线路的传输功率增量ΔPtr：

式中：U、U′分别为机端电压幅值和传输线末端电压幅值；ΔPout为IIG 有功输出增量；Δδ为暂态期间机端电压相位增量。鉴于常规控制下IIG 仅输出有功功率，因此故障暂态期间常规控制的IIG 机端电压相位变化趋势与机组有功输出间近似呈线性关系，即dδ/dt与dPout/dt成正比。

基于上述推导，可对故障暂态期间不同故障控制策略下IIG 机组端电压相位变化做如下假设：

式中：δ0、δf分别为机组端电压相位故障前后稳态值；ε（t）为单位阶跃。借助式（6）可实现IIG 输出电流向统一参考系下的动态相位换算。

1.3 基于暂态电流回代的系统方程暂态修正

为避免构建高阶难解的动态方程［21］，本节提出了一种针对多IIG 接入系统方程的暂态修正方法。针对故障暂态分析，构建时变的节点阻抗矩阵，从而使节点电压与注入电流在形式上仍保持线性关系，使方程具有可解性。

传统系统方程如式（12）所示，仅适用于表征稳态下节点电压所构成向量U与注入电流所构成向量I间的数值关系。

式中：Z为稳态节点阻抗矩阵。

故障暂态期间线路元件在dq旋转坐标系下的伏安特性为：

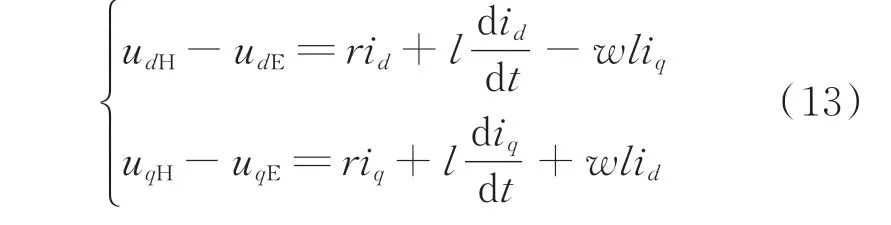
式中：udH、uqH分别为线路首端电压d、q轴分量；udE、uqE分别为线路末端电压d、q轴分量；r、l分别为线路电阻、电感值；w为电角速度。

线路阻抗z的计算公式如式（14）所示。

即故障暂态期间线路等效阻抗为稳态阻抗与暂态附加项之和，后者与线路流过的暂态电流值相关。通过对系统内各线路阻抗进行暂态修正，即可得到适用于暂态分析的等效节点阻抗矩阵Z（t）。暂态期间各节点电压与注入电流向量间通过时变的Z（t）仍保持线性映射关系，节点暂态电压即可线性求解。利用暂态电压即可通过式（16）进一步得到故障点处暂态电流iF。

式中：RFault为故障接地电阻；uF为故障点处电压；ZFk为Z（t）中第F行（故障节点对应行）、第k列对应元素（这里阻抗矩阵元素为经过暂态修正后的时变量）；ik为节点k处接入的IIG 暂态输出电流（对于无电源接入的联络节点其对应电流值为0）。

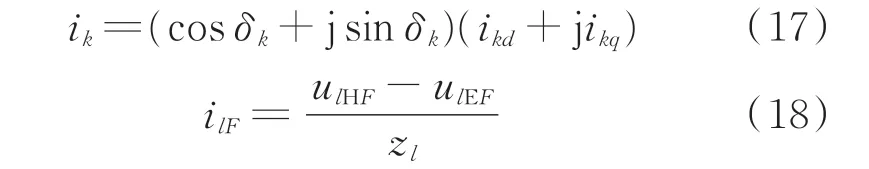
式中：δk为节点k的暂态电压相位；ikd和ikq分别为节点k接入的IIG 电流d、q轴分量的局部量；ilF为线路l流过的暂态电流；ulHF和ulEF分别为线路l首端和末端的暂态电压；zl为线路l的暂态等效阻抗。

利用式（18）可求解系统内任意线路的故障暂态电流，从而为保护设计提供支持。综上，基于IIG 暂态电流回代的系统级故障暂态解析方法［22］具体流程如图3 所示。

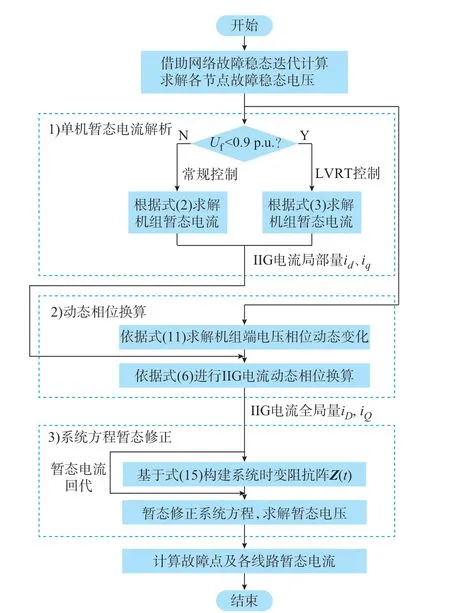
图3 系统级故障暂态解析流程图Fig.3 Flow chart of system-level fault transient analysis

2 仿真验证

为验证本文所提的系统级故障暂态解析方法的有效性，在PSCAD/EMTDC 中搭建了有6 台IIG（IIG1、IIG2、…、IIG6）接入的IEEE 33 节点仿真系统，线路参数详见文献［23］。不失一般性，在母线8、12、15 和32 分别接入4 台双级式光伏电源，在母线7 和24 分别接入2 台直驱风机，如图4 所示。考虑实际各接入机组容量可能存在差异，设置IIG3、IIG4 的额定有功功率为300 kW，其余机组有功功率均为100 kW，各IIG 控制参数见附录A 表A1，参数整定原则参照文献［24］。以节点17 处发生三相经1 Ω 过渡电阻接地短路故障为例，进行系统故障暂态计算。

图4 IEEE 33 节点仿真系统拓扑Fig.4 Topology of IEEE 33-bus simulation system

根据稳态计算方法［19］计算并汇总故障稳态数据如附录A 表A2 所示。IIG3 和IIG4 距离故障点较近，故障后节点电压分别为5.274、2.308 kV（小于90%额定值），这两台机组进入LVRT 控制；IIG1 和IIG2 故障后端电压依然高于90%额定值，故障期间处于常规控制；IIG5 和IIG6 距离故障点较远，故障期间输出几乎未受影响。在此基础上，进行多IIG接入系统的故障暂态计算。需要注意，鉴于本文所提暂态解析方法是基于旋转两相坐标系下分析的，网络内各三相电气量均需经Park 变换换算至统一坐标下，本仿真中采用外电源等效内电势E为坐标参考。

2.1 各IIG 故障暂态电流与相位换算验证

以IIG2 与IIG4 为例对1.1 节单机暂态电流解析结论进行计算验证。

对于距故障点较远的IIG2，故障后其接入节点电压降落至8.306 kV（稳态电压的0. 904），故障期间该机组保持稳态工况下常规双闭环控制。故障后端电压降落，将导致IIG 机组直流侧功率出现不平衡态，从而导致直流电压经历先抬升后降落的暂态过程，进一步地通过双闭环控制对交流侧电流输出产生影响。

附录B 图B1、图B2 分别为IIG2 直流电压udc和端电压参考系下交流电流d、q轴分量波形的仿真值与计算值对比（电流d、q轴分量均为故障暂态电流瞬时值），忽略直流电压仿真值毛刺，其计算结果与仿真值误差较小。直流电压仿真值中的高频分量来源于电力电子元件的高频通断，本文不对此深入讨论。

对于距离故障点较近的IIG4，故障后端电压跌落严重，逆变器控制切换为LVRT 控制。根据LVRT 策略计算可得，故障后d、q轴电流指令值分别为0.446 8 kA 和0.623 8 kA，在内环调制作用下交流侧输出电流迅速跟踪指令值，如附录B 图B3 所示。单机故障暂态电流波形与电磁仿真波形基本重合，验证了前文单机解析的正确性。

将计算所得IIG 故障暂态电流局部量动态换算至系统统一参考系。根据式（11）可得：

式中：δ2、δ4分别为IIG2 和IIG4 机端节点暂态 电压相位；δ20、δ40、δ2f和δ4f分别为IIG2 和IIG4 机端节点电压相位故障前初值和故障稳态值；r21为IIG2 暂态电流的衰减系数。

IIG2的衰减系数r21、r22分别为35.309 和595.831。同时计及机端升压变压器变比10 kV/0.38 kV，可得统一参考系下IIG2、IIG4 的电流波形，分别如附录B图B4、图B5 所示。相位差异问题在IIG4 的暂态波形对比（图B3 和图B5）中较为明显。从电流曲线对比可直观看出，相位换算前后IIG4 输出电流的d、q轴分量比例存在差异，这说明已有IIG 单机暂态解析结论（式（2）和式（3））须借助本文所提动态相位换算至统一旋转坐标下才能进行多机系统故障暂态计算。

2.2 故障点及线路暂态电流计算验证

本节通过对故障点处及网络内暂态电流分布进行计算验证，以展示所提方法的系统级解析效果。将各IIG 故障暂态电流全局量回代入暂态修正后的系统方程，求解节点电压暂态，从而进一步根据式（16）和式（17）分别求解故障点及各线路暂态电流。附录B 图B6 为故障点暂态电流的d、q轴分量的仿真与计算结果对比，其相位参考为系统电源内电势E。由图B6 可见采用现有稳态计算方法［19］的故障电流计算结果与仿真电流波形区别很大，其暂态解析精度无法满足全时域量保护（如波形相似度保护）的研究需求。对2 种方法下故障点处三相电流iA、iB、iC的计算结果进行对比，结果如图5 所示。图5（a）为本文所提系统级故障暂态解析方法计算值与仿真波形对比，图5（b）为现有多机稳态计算方法［19］计算值与仿真波形对比。对比结果直观地说明本文所提方法对于故障点处暂态电流解析的有效性。

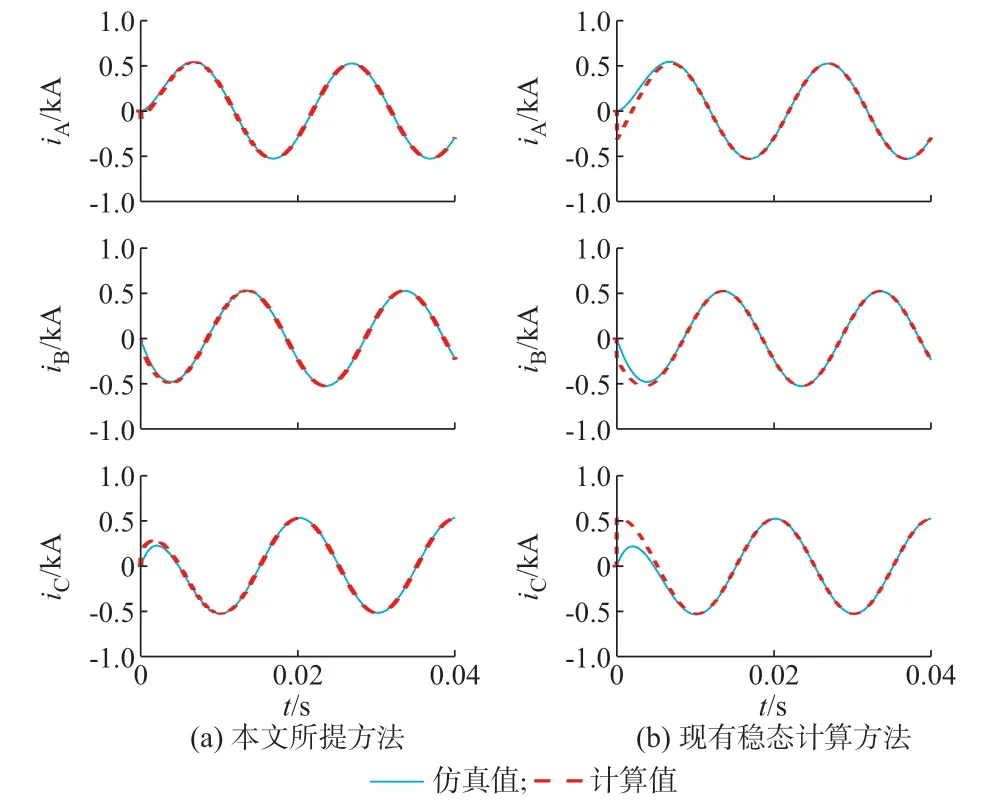
图5 故障点处三相暂态电流计算结果对比Fig.5 Comparison of calculation results of three-phase transient currents at fault point

不失一般性，从仿真系统中选取了3 条非故障线路3-4、9-10 和16-17，对其暂态电流进行仿真验证，结果如附录B 图B7 所示。线路暂态电流计算值与仿真值间误差较小，说明本文所提方法具有针对多IIG 接入网络的系统级故障暂态解析计算能力，可为基于线路电气量的保护研究提供较为可靠的依据。

2.3 误差分析

为进一步量化分析本文所提解析算法的计算精度，对故障后10 ms 内暂态期间故障点电流与线路暂态电流的计算误差进行分析。为合理评估暂态电流计算精度，分别取故障后10 个离散时刻（间隔10 ms）计算各电流量的瞬时误差：

对10 个时刻的瞬时误差求均值可得到该电流暂态计算波形的平均误差。汇总线路3-4、9-10 和16-17 以及故障点处暂态电流的10 ms 内计算和仿真值结果以及各暂态电流计算结果平均误差如附录B 表B1 所示。可见，本文所提解析方法可对多IIG接入系统的故障暂态实现精确计算，故障后10 ms内电流解析结果平均误差均低于5%。

3 结语

本文提出了一种针对高比例可再生能源接入的系统级故障电流全时域解析方法。通过对IIG 暂态输出电流的动态相位换算和系统方程的暂态修正，为现有IIG 单机暂态解析结论用于多机系统计算提供了桥梁，解决了多机系统动态方程的高阶难解问题，实现了对多机系统故障点及线路暂态电流的精确解析。仿真验证结果表明所提方法对故障后10 ms内暂态电流的平均计算误差低于5%，可为全时域量保护的设计与定值整定研究提供较为可靠的依据。

本文研究的计算精度受IIG 单机解析结论影响以及未考虑不对称故障解析计算，后续工作将展开进一步研究。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。