基于改进生成式对抗网络的电气数据升频重建方法

李富盛，林 丹，余 涛，王克英，吴毓峰，杨家俊

（华南理工大学电力学院，广东省广州市 510640）

0 引言

物联网的目的之一是实现不同对象间的物理连接与信息交互［1］，对数据采集、数据清洗［2］、数据通信［3］、数据高级应用［4］等方面提出更高的要求。信息与通信技术是提高电网自动化水平的重要手段，也使电网产生大量高频和低频数据［5］。相比于低频电气数据，高频电气数据具有更丰富的多源异构的特征，能够更清晰地反映用户用电行为，形成更准确的用户画像和标签体系。其次，高频电气数据涉及更多的维度，能够提高相关性挖掘能力，提升预测水平。另一方面，由于通信和储存技术限制，高频数据常通过压缩感知技术转化为低频数据，应用前再进行 升 频 重 建（frequency-increased reconstruction，FIR），还原数据细节［6］。同时，如果数据采集与监控（SCADA）系统［7］将高频数据压缩为低频后再传输，则能在受到信息攻击后通过数据重建而降低数据损坏程度。综上，升频重建是提高数据质量和挖掘电网数据潜在价值的支撑技术之一。

电气领域中已有的重建算法着力于缺失片段重建问题［8-10］，而不是提高数据的采样频率（即升频重建）。例如，文献［8］利用一维电气数据和基于浅层神经网络的生成式对抗网络（GAN）［11］实现高精度的缺失片段重建，但未讨论该模型在升频重建问题的适用性。缺失片段重建问题一般是整体完整、局部缺失，为了保证重建精度，缺失片段的数据量一般不超过原始数据总量的50%，即重建倍数不超过2 倍［8］。而升频重建的目的在于提高整个数据集的采样频率，重建倍数一般不低于2 倍。

目前，电气领域常用插值方法对一维时序电气数据进行升频重建［12-13］，但重建精度不高，且缺乏高频细节。图像领域的超分辨率重建方法主要有3 类：基于插值的方法［14］、基于建模的方法［15-16］和基于学习［17］的方法，但这些方法的高频细节还原度不高。近年来，GAN 在图像、文本、能源等领域取得突破性进展［18-21］。因此，有必要设计一种将一维时序电气数据转化为电气图像的方法，利用GAN 在图像超分辨率重建问题的优势，提高电气数据的升频重建精度。同时，电气数据升频重建涉及数据从低维向高维转化，是一个具有大量可能解的高病态逆问题［22-23］，有必要设计适用于该问题的GAN 的生成器、判别器和损失函数。

综上，为了解决低频电气数据的升频重建问题，提高重建精度和高频细节还原度，本文设计了电气数据转化为电气图像的方法，引入了GAN，损失函数考虑对抗损失、实际损失、感知损失和电气图像的低维特征或高维特征，生成器引入了深层残差网络并对残差块（residual block）进行改进。最后，以国外公开可用的数据集为例，验证所提方法的有效性。

1 基于GAN 的电气数据升频重建

1.1 新型数据通信机制

近年来智能电表项目被大力推广，但国际公开的电力数据集中大部分的采集频率较低，采集周期级别大多为15 min、30 min、1 h 等［24］，只有少数达到了1 min 或者1 s 级别［25-28］。由于电网设备数量大、类型多，导致电气测量数据规模大，高频采样面临投入成本高、通信难度大、数据存储成本高等限制，所以电网已有的数据集一般是低频。传统的数据通信机制是直接传输低频或高频数据。直接传输低频数据会忽略部分数据细节，传输高频数据会增大通信和储存的压力。

显然，该模式难以满足数据量激增的现代电网的要求。因此，本文提出一种新型数据通信机制，高频数据在数据发送端压缩为低频，低频数据在数据接收端就地进行升频重建。该模式解决了传统模式的不足：一是分布式的数据处理方式减轻了数据中心的计算和存储压力；二是通信网只需传输低频数据，相同带宽下可以传输更多的数据集，通信效率高。

1.2 数据升频重建的总体框架

本文设计了低频电气数据的升频重建框架，如图1 所示。

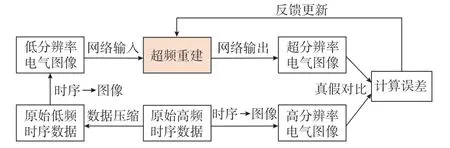
图1 数据升频重建的总体框架Fig.1 Overall framework of data FIR

首先对原始高频数据集下采样得到低频数据集，然后将时序形式的电气数据转化为电气图像，利用电气图像进行升频重建，最后比较升频数据集与原始高频数据集的误差，根据误差反馈更新重建模型的参数。本文中“高频”不是绝对的，而是相对的概念。升频重建是指将数据采样频率以一定的重建倍数进行提高。本文定义仿真用的原始数据为高频数据，对原始数据进行下采样得到低频数据，重建后的数据称为升频数据，升频数据与高频数据的采样率相同。此外，原始数据采样率的高低不是限制本文方法的因素。

1.3 电气数据转化为电气图像

为了充分利用先进机器学习方法在图像特征提取上的优势，本文设计了电气数据转化为电气图像的通用方法。设高频电气数据集有L个采样时刻，每个采样时刻有n种类型的电气数据，包括有功功率、无功功率、电压、电流、频率、功率因数等，则高频电气数据集可以表示为L×n的矩阵。每张电气图像的n个通道分别对应电气数据的n种类型。图2和附录A 表A1 分别为时序数据转化为电气图像的示意图和步骤。图2 中，l为电气图像每个通道的边长。电气图像形式不改变时序形式的数据大小，仅改变数据的排列位置。电气图像的颜色深浅与时序数据的大小正相关，其纹理变化与时序数据的变化趋势正相关，根据电气图像能够从视觉上比较高频细节还原度。

图2 时序数据转化为电气图像示意图Fig.2 Schematic diagram of transforming time series data into electrical image

1.4 GAN

GAN 通过生成器生成超分辨率电气图像，再通过判别器从大量可能解中筛选出与实际情况差异最小的生成样本，从而解决高病态逆问题，实现高精度重建［29］。GAN 只是一种框架，其生成器和判别器的内部算法、连接方式、损失函数等在不同的问题上会有较大的区别。

设已有高分辨率电气图像集、低分辨率电气图像集和超分辨率电气图像集分别为xHR、xLR和xSR，其数据单元分别为xHRj、xLRj和xSRj，其中xSRj表示生成器GθG以xLR为输入得到的生成样本，xSRj也可以表示为GθG(xLR)，其中θG为生成器参数。判别器输入为生成样本或真实样本，输出为输入被判定为真实样本的概率，为DθD(GθG(xLR))或DθD(xHR)，其中θD为判别器参数，DθD(xSR)或DθD(xHR)分别表示判别器DθD以xSR或xHR为输入得到的输出。基于GAN的升频重建架构如附录A 图A1 所示。

1.5 生成器

1.5.1 生成器结构

电力系统是巨维且复杂的，其电气数据具有高维潜在特征。一般思路是引入深度神经网络对电气数据进行特征挖掘，但是由于深度神经网络存在梯度消失问题，本文引入学习能力更强的深度残差网络（DRN）作为生成器。DRN 内部的残差块使用了残差跳跃式的结构，打破了深度神经网络某一层的输出只能给下一层作为输入的惯例，使某一层的输出可以跨过几层作为后面某一层的输入，缓解了深度神经网络深度增加带来的梯度消失问题，并能通过叠加多层残差块提高模型的特征学习能力和准确率［30］。生成器结构如图3 所示。其中，K为重建倍数。为了加速训练，利用VGG-19 模型［31］的预训练结果初始化DRN。

图3 数据升频重建的生成器结构Fig.3 Structure of generator for data FIR

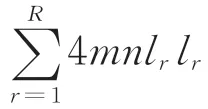
1.5.2 生成器损失函数

为了提高重建精度和高频细节还原能力，生成器损失函数设计为以下几种损失函数的加权组合。

为了使得生成器能够欺骗判别器，生成对抗损失lGen考虑了判别结果，计算如下：

实际损失为生成样本和真实样本的均方误差（MSE），定义为lMSE，其表达式为：

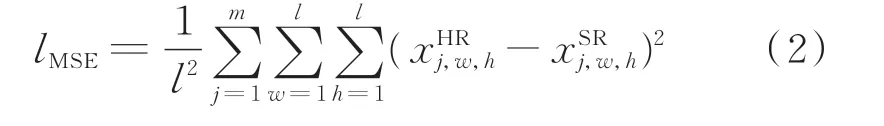
式中：w和h分别为每一个通道中矩阵的宽和高；h和分 别 为 第j个 真 实 样 本、生 成 样 本 的 每个通道矩阵中宽为w和高为h的像素点的数值。

使用实际损失训练生成器会导致生成样本过于平滑，重建结果过于保守，不利于高频细节的还原。因此，本文引入感知损失衡量生成样本和真实样本在局部特征上的差异。具体地，考虑到VGG-19 模型具有提取电气图像局部特征的能力，本文在已经训练好的VGG-19 模型中分别输入生成样本和真实样本，并提取电气图像的特征图φa，b，其中φa，b的含义为VGG-19 模型在第a次池化操作之前得到的第b个特征图。本文将真实样本特征图和生成样本特征图在对应位置上各像素点数值的均方误差定义为感知损失lVGG。对于基于低维特征的本文方法，感知损失使用特征图φ2，1进行计算，对于基于高维特征的本文方法，感知损失使用特征图φ5，4进行计算。lVGG的计算公式为：

1.6 判别器

1.6.1 判别器结构

DCN 作为判别器，能够实现真实样本与生成样本的有效分类。生成器实现以假乱真，而判别器实现去伪存真。通过二者的对抗博弈，生成器的生成能力和判别器的判别能力会同步提高，使得生成样本更接近真实样本，最终实现更高的重建精度。判别器结构如附录A 图A3 所示。

1.6.2 判别器损失函数

为了使得判别器能够辨别真假，判别对抗损失lD考虑了判别结果，计算式如下：

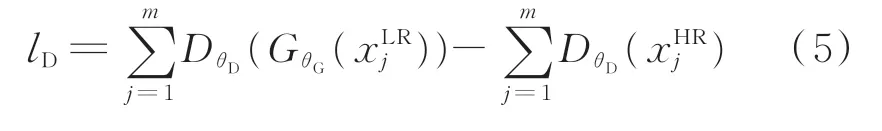
2 仿真实验

本章通过3 个案例验证所提升频重建方法的效果。案例1 对比本文方法与其他方法的高频细节还原度；案例2 对比本文方法与其他方法的重建精度。案例3 研究本文方法对同一个地理位置的不同数据集的泛化性。

迭代次数设为5 000 次，使用Adam 优化器，初始学习率设为1×10-4，Adam 优化器的一阶矩估计的指数衰减率设为0.9，每500 次迭代后学习率变为原来的1/10。

2.1 数据准备

2.1.1 缺失值填补

截取数据量比较完整的片段作为实验数据。由于每个缺口的缺失数量对数据总量而言可以忽略，本文使用线性插值方法进行缺失值填补。

2.1.2 归一化处理

为了提高电力图像的可视化效果，先利用最大最小归一化方法将电气测量数据的取值范围调整为［0，1］，然后所有数据乘以255，变换到图像处理的常用取值范围［0，255］。相同类型电气数据在归一化和反归一化中使用相同的最大值和最小值。

2.1.3 仿真用数据集

以国外公开可用的数据集I-BLEND［28］为例，对3 个案例进行仿真验证。I-BLEND 是某大学校园内不同建筑的用电数据集，建筑类型包括教学楼、图书馆、设备房、报告厅、男生宿舍、女生宿舍和餐厅，采样时长为52 个月（每座建筑的单个电气量的数据集为200 万数量级），电气参数包括电压、电流、功率、频率和功率因数，采样频率为1 min。仿真用的数据集片段截取为当地时间2014-01-08T00：00 到2015-05-02T23：59，共有691 200 个采样点，建筑类型为教学楼、男生宿舍、女生宿舍和餐厅，电气参数为有功功率、电流和电压。

本文取低频和高频电气测量数据的采样频率分别为15 min/次和1 min/次。为了方便构造电气图像，在高频电气测量数据的每15 个数据后添加一个0 值，使重建倍数K变为16，K的结果为整数。加零操作不会对低分辨率电气图像造成影响。根据上述处理，每64 h 的电气测量数据转化1 张电气图像。本文仿真中，高分辨率电气图像和重建后的超分辨率电气图像的大小均为64×64×3，低分辨率电气图像的大小为16×16×3。每个数据集都转化为180 张高分辨率电气图像和180 张低分辨率电气图像，并按照8∶1 的比例划分训练集和验证集。

2.2 数据重建精度评估指标

2.2.1 时序数据层面

平均绝对误差（MAE）的范围为［0，+∞），MAE 越小，误差越小，计算式如下：

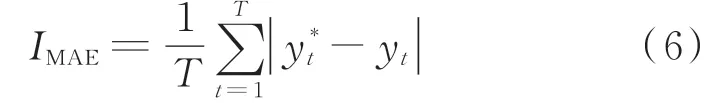
式中：IMAE为MAE 值；、yt分别为验证集的原始时序电气数据和重建时序电气数据，其中t表示验证集的第t个数据；T为验证集的数据总量。

平均绝对误差百分数（MAPE）的范围为［0，+∞），MAPE 越小，误差越小，计算式如下：

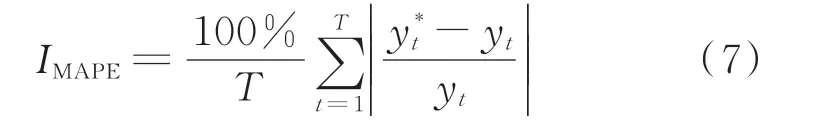
式中：IMAPE为MAPE 值。

2.2.2 图像层面

峰值信噪比（PSNR）［34］是重建领域的常见评价指标。PSNR 常用MSE 定义，即基于像素点的误差进行图像质量评价。PSNR 通过非线性运算将MSE 转化为单位为dB，范围为（-∞，+∞）的值。根据文献［23］，当前技术水平下可认为PSNR 大于20 dB 为较高的重建精度。PSNR 的计算式为：

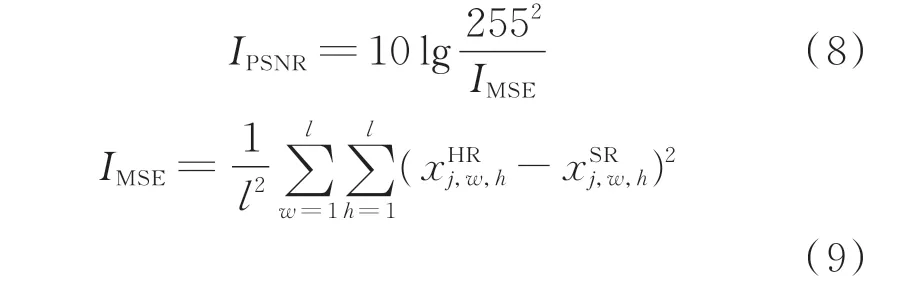
式中：IPSNR为PSNR 值；IMSE为MSE 值。

电气图像是高度结构化的，相邻像素之间有很强的关联性。结构相似性（SSIM）［35］可以抵消MAE 和MAPE 无法衡量图像结构相似性的缺陷。SSIM 从图像组成的角度将图像信息定义为亮度、对比度和结构3 个不同因素的组合，用均值作为亮度的估计，标准差作为对比度的估计，协方差作为结构相似程度的评估指标，详细推导参考文献［35］。SSIM 的简化计算式如下：

由1.3 节可知，电气时序数据的变化趋势和数值分别对应电气图像的纹理和色调。SSIM 值的范围是［0，1］，越大表示电气图像的纹理与色调越接近，即时序形式的电气数据的变化趋势与数值越接近。

2.3 高频细节还原度评估

对双三次插值（BI）［36］、传统GAN［8］和深度卷积神经网络（DCNN）［31］以及本文基于低维、高维特征的数据重建方法进行高频细节还原度评估。

2.3.1 电气图像

以教学楼数据集为例，附录A 图A4 为电气图像形式的重建结果。高分辨率电气图像在视觉上具有丰富的高频细节和清晰的纹理。插值重建的电气图像虽然像素增大了，但是在视觉上趋于平滑，重建效果相对保守，表明了插值重建方法不具备高频细节还原能力。采用传统GAN 和DCNN 方法重建的电气图像比插值方法有更清晰的纹理，但是与原始高分辨率电气图像相比，整体色调以及局部纹理细节仍有明显差别。基于低维特征或高维特征的超分辨率电气图像的高频细节还原度都很高，其生成的纹理和色调与高分辨率电气图像高度相似，但是基于高维特征的电气图像比基于低维特征的电气图像具有更丰富的纹理。

2.3.2 时序数据变化曲线

以教学楼数据集为例，将验证集的电气图像还原为时序形式的电气测量数据，数据重建结果如图4 所示。采用本文方法得到的重建曲线与真实曲线相比，除了个别区间的峰值较低或谷值较高外，2 条曲线的变化趋势基本相同，整体重建效果良好。

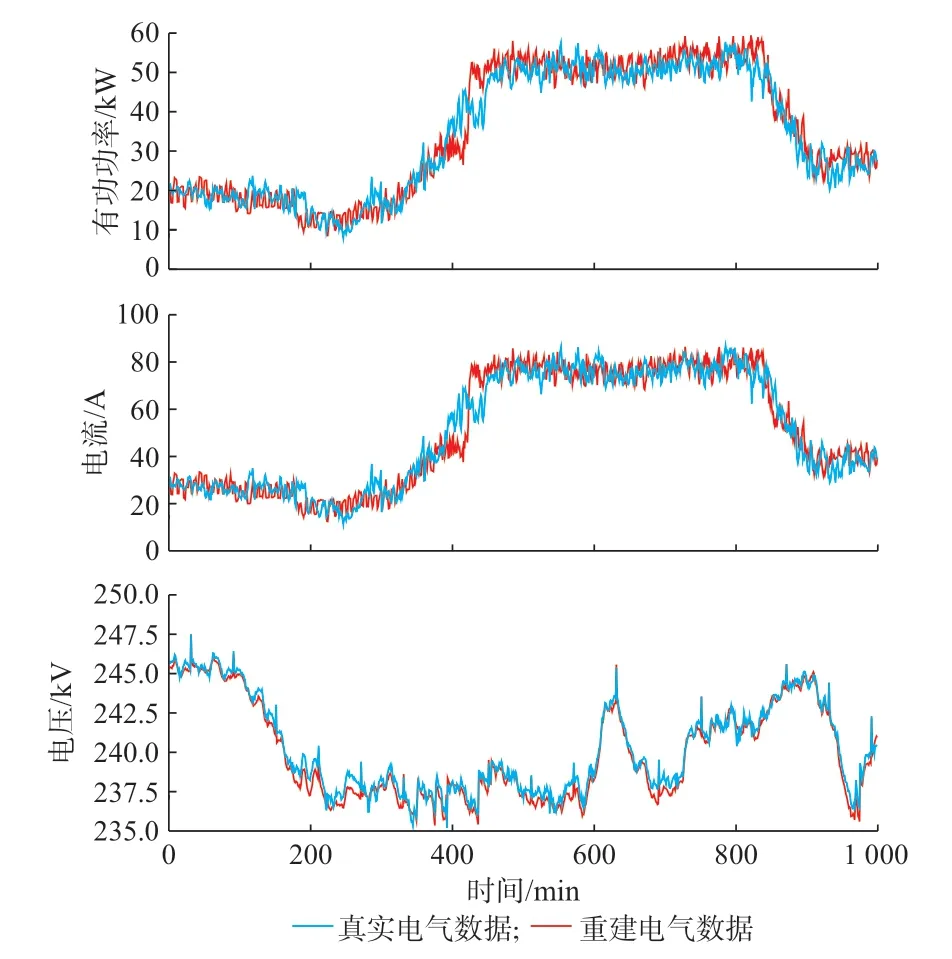
图4 数据FIR 结果Fig.4 Results of data FIR

2.4 数据重建精度评估

由于高频细节的多样性和随机性，侧重于对点与点之间的片段进行重建会导致无穷多解。因此实现重建应该分两步走，先重建整体相似的分布，再还原高频细节。GAN 能够学习原始数据的潜在分布，有助于对解空间进行降维，再加上本文设计的提高高频细节还原能力的手段，最终实现高精度重建。以下从分布相似性和评估指标方面进行重建精度评估。

2.4.1 分布相似性

本研究验证了重建数据具有与真实数据相同的统计特性。图5 为关于教学楼有功功率的真实数据和重建数据的累积分布函数（CDF），即小于等于当前数据值的所有数据的概率分布。对于给定的数据集，累积分布函数是唯一的，不会丢失任何数据信息。由图5 可见，重建数据的累积分布除了峰值较低或谷值较高外，其他部分与真实数据的累积分布基本相同。此外，本研究利用JS 距离［37］计算真实数据与重建数据的累积分布的相似程度。JS 距离是信息论中常用于衡量概率分布相似性的指标，取值范围为［0，1］，越接近0 表示两分布差异越小。本实验的JS 距离计算结果为0.18，接近于0，表明真实数据和重建数据的累积分布有小部分存在差别，但整体相似度较高。

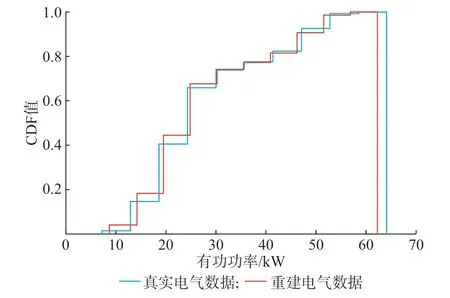
图5 CDF 评估结果Fig.5 CDF assessment results

2.4.2 评估指标

根据式（7）至式（11），计算验证集的评估指标。表1 为在单次验证中各项指标的平均评估值，表2为在单次验证中各图像的各个指标评估值。可见，针对不同建筑的电气数据集，插值重建方法的PSNR 和SSIM 的数值都比较小，表明该方法无法有效挖掘电气数据的数据结构关系，高频细节还原能力不足。插值重建方法的MAE 和MAPE 的数值都比较大，表明该方法重建精度较低，无法准确还原高随机性的高频细节。传统GAN 方法的PSNR 不是特别突出，SSIM 比较高，表明传统GAN 方法能够在一定程度上挖掘电气数据的数据结构关系，但是没有经过改进的GAN 的高频细节还原能力不理想。传统GAN 方法和DCNN 的MAE 和MAPE 在3 种方法中处于中间水平，表明该方法具有一定的重建精度。相对地，本文方法的PSNR 比较高，表明该方法的重建结果失真比较小。超分辨率重建方法的SSIM 接近1，表明该方法能够有效地重建电力图像的纹理和色调，即能够学习到电气测量数据的结构关系，进而有效地还原高频细节。本文方法的MAE 和MAPE 与其他2 种方法相比最小，重建精度最高。对于本文方法，基于高维特征的重建结果比基于低维特征的重建结果具有更高的PSNR、SSIM和更低的MAE、MAPE，表明基于高维特征的数据重建方法更适用于本研究的数据集。

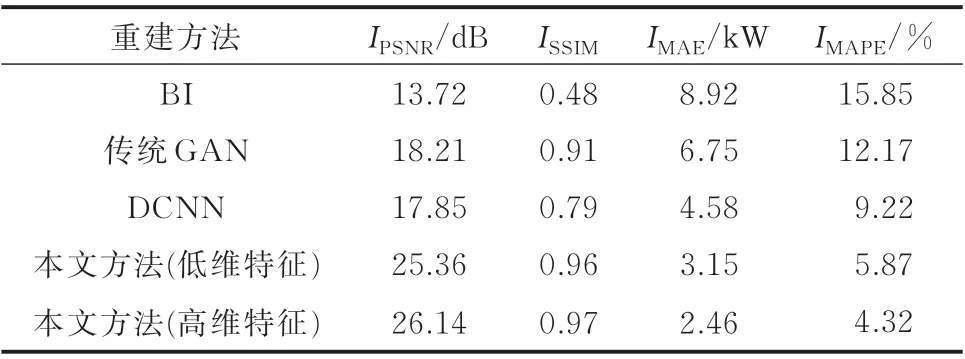
表1 不同方法的数据FIR 精度Table 1 Data FIR accuracy of different methods

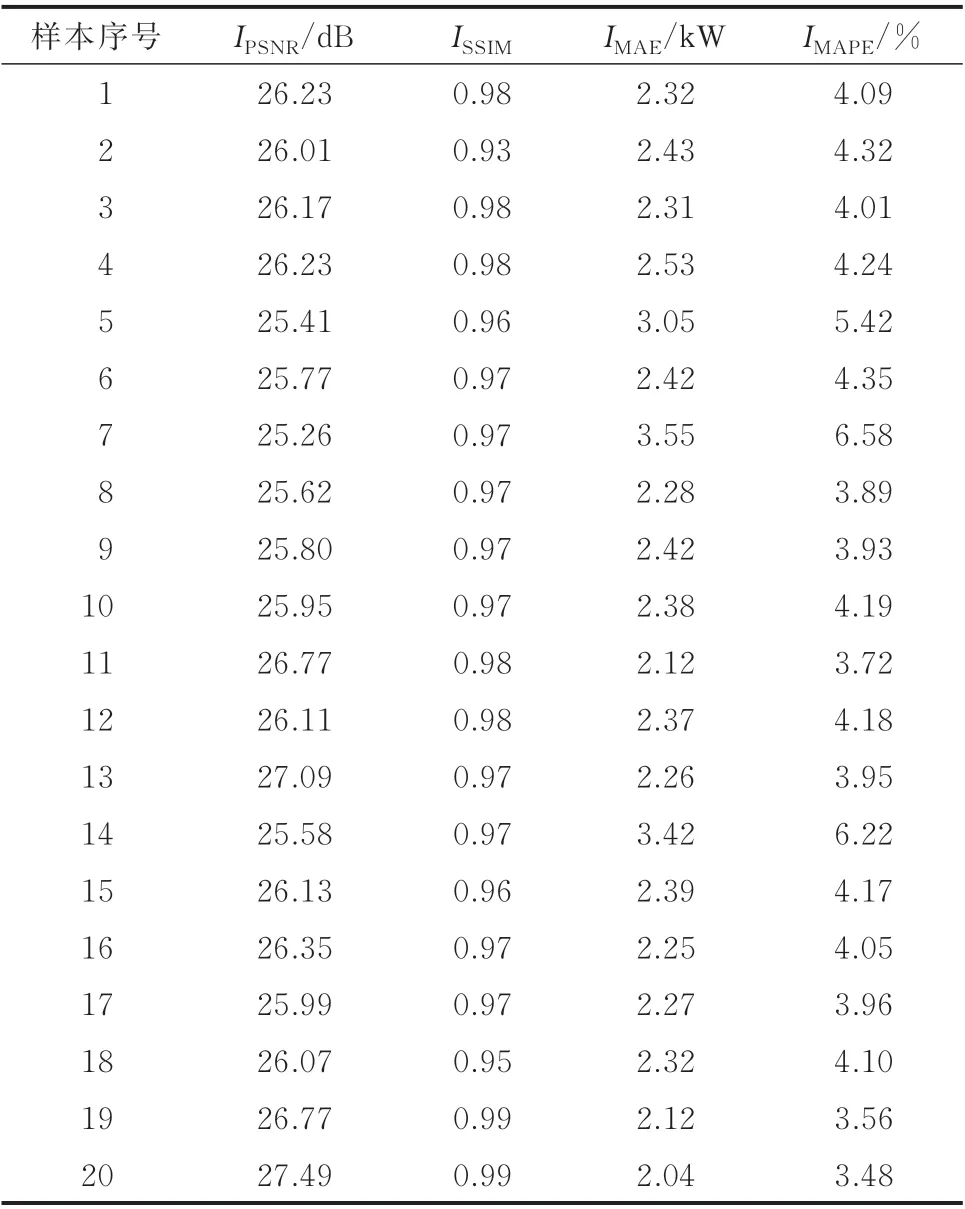
表2 基于高维特征的数据FIR 精度Table 2 Data FIR accuracy based on highdimensional features

2.5 重建模型在区域内不同数据集间的泛化性

为了研究相同地理位置下不同建筑的电气数据单独训练得到的模型对于其他建筑的泛化性，本节将上文中教学楼、男生宿舍、女生宿舍和餐厅的生成器作为已训练的重建模型，将4 个建筑的验证集交叉输入到4 个重建模型中，得到新的超分辨率电气图像。附录A 图A5 为某一验证集在区域内不同数据重建模型下的升频重建结果。结果表明，教学楼和女生宿舍的验证集，在教学楼重建模型和女生宿舍重建模型上都能恢复相似的纹理和色调。类似地，男生宿舍和餐厅的验证集，在男生宿舍重建模型和餐厅重建模型上都能够恢复相似的纹理和色调。不同建筑模型之间存在泛化性是因为GAN 从不同建筑数据集学到了相似的潜在分布。用电数据的潜在分布与用电行为是强关联的，因此，I-BLEND 数据集中，教学楼和女生宿舍具有相似的用电行为，男生宿舍和餐厅具有相似的用电行为。

除了视觉上对高频细节还原度的比较，附录A表A2 展示了区域内不同数据集的重建精度评估结果。教学楼和女生宿舍验证集，在教学楼重建模型和女生宿舍重建模型上均具有较高的PSNR、SSIM和较低的MAE、MAPE。男生宿舍和餐厅验证集，在男生宿舍重建模型和餐厅重建模型上，均具有较高的PSNR、SSIM 和较低的MAE、MAPE。结果表明，本文方法能够在相同区域内的不同数据集间进行泛化。

3 结语

本文将改进GAN 应用于低频电气数据的升频重建问题，其主要贡献如下：

1）设计了时序形式的电气数据转化为电气图像的方法，利用先进神经网络方法实现了对电气图像特征的高效挖掘；

2）通过采用基于深层残差网络的生成器解决了深度神经网络的梯度消失问题，通过设计残差块的结构降低了计算复杂度，并在生成器损失函数中考虑电气图像的低维特征或高维特征，提高了生成器学习能力；

3）本文方法是基于数据驱动的无监督训练方法，具有一定的通用性，仿真结果表明该方法在相同的模型参数下能够对不同的数据集实现高精度升频重建，且训练好的重建模型对同一个地理位置的不同数据集具有可泛化性。

本文未将数据压缩与重建方法进行综合考虑，且未研究对不同地区的电气数据集均具有泛化性的升频重建方法，未来需要进一步加深该方面研究。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。