基于虚拟能量变化率的谐振接地系统高阻接地故障选线方法

王尊贤，武守远，栾晓明

（山东大学电气工程学院，山东省济南市 250061）

0 引言

在配电网接地故障中，高阻接地故障发生的比例可达10%左右［1-2］。常见的高阻接地介质包含沙地、草地、水泥和树枝等，过渡电阻通常在几百欧到几十千欧范围［3］。在目前中国配电网采用的中性点接地方式中，谐振接地系统的非高阻故障检测定位的理论及应用已较为成熟，但对于高阻故障，这些方法一般在过渡电阻达到2 kΩ 以上时可靠性就难以保证［4］。

高阻接地故障高频暂态特征会随着过渡电阻升高而逐渐衰减［5］，且故障具有发展性，在故障初始阶段过渡电阻较高可达几十千欧以上，待接地点表面不断烧蚀、碳化后其值逐渐降低。因为高阻故障信号在过渡过程中幅值较低且存在非线性特征，故障定位较为困难。考虑系统中三相对地参数不对称，可能会导致非故障线路的零序分量较大［6］，与故障线路混淆进而造成误判。

为解决高阻接地故障检测难、精度差的问题，国内外专家学者提出了一系列针对稳态和暂态分量的检测及选线方法［4，7］。基于稳态分量的选线方法一般适用于过渡电阻较低时的接地故障，此时故障的稳态分量含量大且易提取，但是消弧线圈的过补偿可能会改变稳态电流分布，造成故障特征消失，导致无法检测出故障。5 次谐波法［8-10］在故障电阻超过1 kΩ 时难以提取5 次谐波；负序分量法［11］受系统三相不平衡的影响较大。文献［12-13］利用线路零序分量计算线路能量流动方向来选线，在故障电阻达数千欧时也有一定的效果，但是对测量设备的精度要求较高。故障时暂态分量相较于稳态分量更加明显，包含的故障信息也更丰富，受消弧线圈的影响也较小［7］。在暂态分量选线算法中，首半波法［14］和暂态零流比幅比相法［15］所需的特征量捕捉时间较短，易受故障电阻和故障初始角的影响；瞬时功率［16］和暂态能量法［17-18］受线路中存在的固有零序分量的影响较大。此外，行波法［19-21］和神经网络算法［22-23］也被应用于高阻故障的选线，取得了一定的效果。

本文从谐振接地系统发生高阻接地后故障线路对地结构参数发生的瞬时和永久性改变着手，总结出暂、稳态过程中故障线路对地电容参数的变化规律，据此构造出反映故障前后对地电容变化的虚拟能量及其变化率，提出了基于虚拟能量变化率的高阻接地故障选线算法的具体判据和选线流程。仿真结果和现场实测数据表明，本文方法具有较高的准确性和适用性，并且与暂态能量法的对比表明其可克服一定程度三相对地参数不对称造成的影响，提高了检测的可靠性。

1 配电网高阻接地故障特征分析

当配电网谐振接地系统发生高阻故障时可近似认为电阻R等于3 倍的实际接地点过渡电阻Rf，此时暂态谐振频率较低，可忽略线路等效电感。当系统电容电流较小或故障点距母线较近时才可能存在过阻尼状态［7，24-25］，系统的高阻故障大部分处于欠阻尼状态，此时过渡电阻值远大于线路的电阻值，为简化运算，可忽略线路电阻［26-27］。据此可建立谐振接地系统发生高阻接地故障时的等效电路图，如图1所示。图中：uf=Umsin(ω0t+φ)为故障虚拟电源，其中，Um为故障相电压幅值，ω0为工频角频率，φ为故障初始角；C0l为第l（l=1，2，…，n）条线路的对地分布电容；ucl为第l条线路的对地分布电容电压；icl为第l条线路的对地分布电容电流；i0l为第l条线路的零序电流；uof为母线零序电压；i0f为流经故障点的零序电流；io为流经中性点的零序电流；L为消弧线圈电感；R为接地故障电阻。

图1 高阻接地故障的等效电路图Fig.1 Equivalent circuit diagram of high-impedance grounding fault

当高阻接地故障发生在图1 中最后一条线路n上时，由其等效电路图可列出：

式中：CΣ为所有线路对地分布电容之和。

求解上式可得故障点的电压为：

谐振接地系统有io=iL，其中iL为流经消弧线圈的电感电流，可列出二阶线性非齐次微分方程为：

该微分方程的特征根p1和p2分别为：

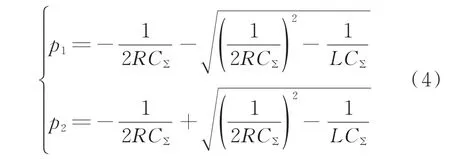
根据接地故障过渡电阻的不同，谐振接地系统会运行在欠阻尼或过阻尼两种状态。

式中：B、Z、A1和A2均为中间变量。

母线的零序电压为：

第k条健全线路的零序电流为：

第n条线路故障后的出口零序电流为：

式中：δ为衰减因子；ω1为自由振荡角频率；A3和A4为中间变量。

母线的零序电压为：

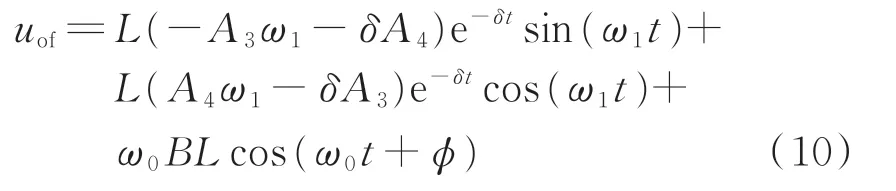
第k条健全线路的零序电流为：

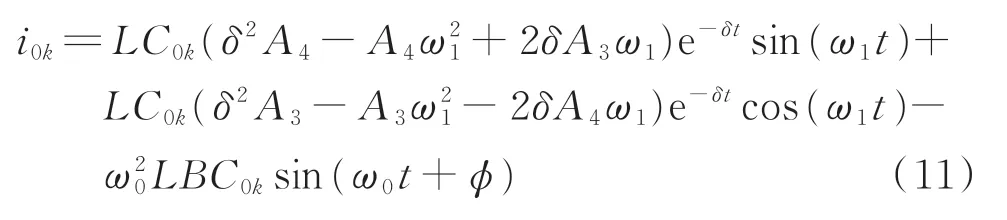
第n条线路故障后的出口零序电流为：

由推导可以看出，在谐振接地系统中过阻尼状态下线路的零序电压和零序电流的分量均为衰减的直流分量和工频稳态分量的叠加，暂态过程持续时间较短；欠阻尼状态下暂态零序电压和零序电流为衰减的交流分量和工频稳态分量的叠加，暂态过程持续时间长。

由零序电压和零序电流暂态分量表达式可见，高阻故障下二者均以衰减因子δ的指数形式衰减，时间常数为τ=1/δ=2RCΣ。因此，达到3 倍时间常数时暂态信号基本衰减至5%左右，可认为暂态过程结束开始进入稳定状态。故障过渡电阻越大，暂态信号的衰减速度越慢，暂态过程持续的时间就越长。

2 高阻接地故障对地电容参数变化分析

2.1 高阻故障对地电容参数变化规律

在接地故障发生时，系统零序网络对地支路的结构改变，其平衡状态被打破，故障线路的对地电容参数发生显著的变化。故障发生后，在过阻尼状态下健全线路对地电容参数基本不变，为：

式中：ik0T为第k条健全线路的零序电流暂态分量；uofT为母线零序电压的暂态分量。

故障线路的对地电容参数i0nTdt/duofT为：

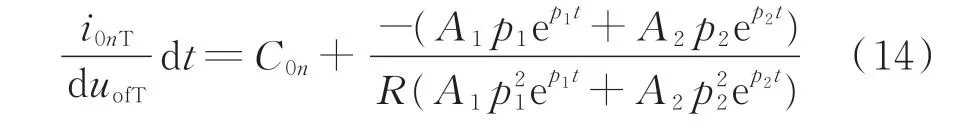
式中：i0nT为故障线路n的零序电流暂态分量。

由式（4）中p1和p2的表达式可得：

则在故障开始时刻式（14）等号右侧最后一项满足：

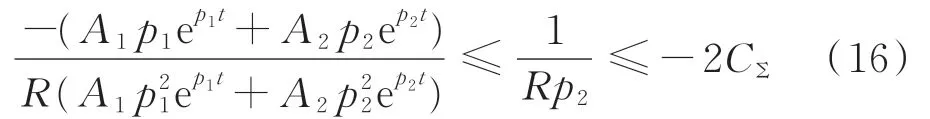
进一步可得：

由上式（17）可知故障线路对地电容参数在故障初期会下降至负值，并伴随着衰减过程最终到达稳定状态。

同理，对于欠阻尼状态，健全线路的对地电容参数等于此线路的对地电容值，同时可求得故障线路的对地电容参数i0nTdt/duofT。

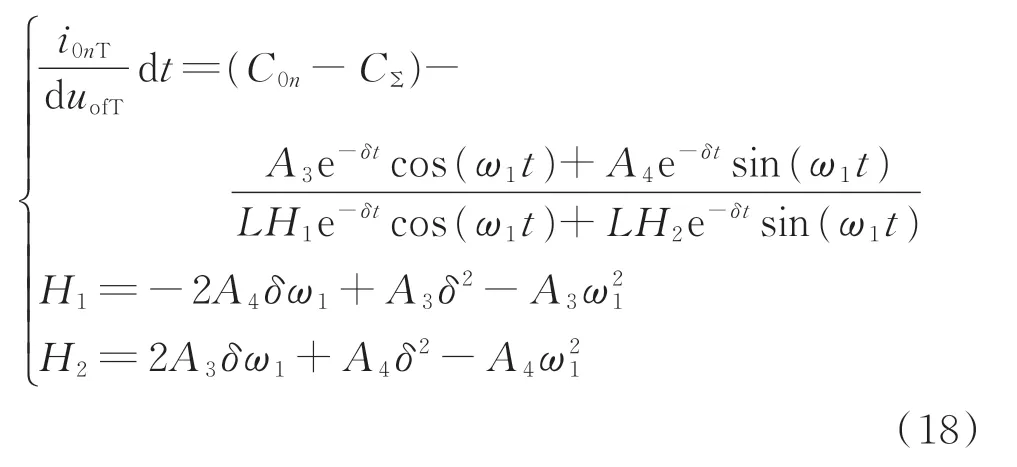
式中：H1和H2均为中间变量。

将式（9）代入式（18）等号右侧中的最后一项分式得：

式 中：RM=2Lδω1e-δt(A3sin(ω1t)-A4cos(ω1t))为衰减的交流分量之差，时间达到3 倍时间常数时基本衰减至零。

在故障开始时刻t=0，代入RM表达式得：

其中

由此可得式（18）满足关系：

欠阻尼状态下，在故障初期暂态过程中故障线路的对地电容参数会发生瞬时性突降的现象，并存在衰减过程。对地电容参数变化量ΔC先迅速增大再逐渐减小，衰减过程受衰减因子δ的影响，其趋势与过阻尼状态基本一致，过渡电阻越大衰减越慢。

一般谐振接地系统采取过补偿方式且过补偿度不超过10%，在系统达到稳态后，故障所在线路的对地电容参数为：

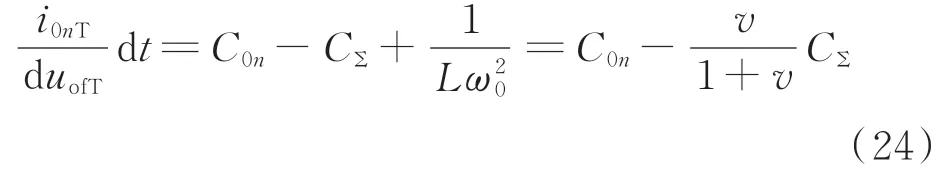
式中：v为系统消弧线圈的脱谐度，通常-0.1≤v≤0。

由此可知，故障暂态过程结束到达稳态后，故障线路对地电容参数会略大于故障前本线路的对地电容值，且此增量会受系统过补偿度的影响。在规定的补偿范围内，过补偿度越高，稳态下线路对地电容参数增量就越大。

2.2 非线性电弧对对地参数变化规律的影响

考虑到在实际故障中高阻接地故障一般伴随电弧的重燃和熄灭，采用基于汤逊空气间隙击穿原理的对数电弧模型［28］来模拟高阻接地故障伴随的非线性电弧现象，将故障支路过渡电阻视为塔基固定电阻和非线性电弧电阻的串联，如图2 所示。图中：R1为塔基固定电阻；R2为非线性电弧电阻；uarc为非线性电弧电阻两端电压。

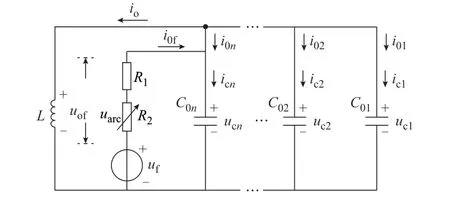
图2 弧光高阻接地故障的等效电路图Fig.2 Equivalent circuit diagram of arc high-impedance grounding fault

对电弧的伏安特性曲线采用二分段线性等效方法，得到电弧电阻的表达式为［24］：

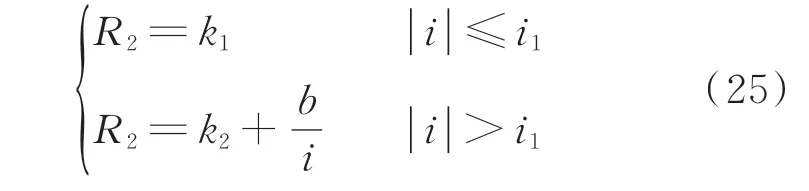
式中：k1为第1 段拟合直线斜率；k2和b分别为第2段拟合直线的斜率和截距；i为电弧电流；i1为分段点电流。

当电弧电阻R2为固定电阻值k1时，总过渡电阻等效为(R1+k1)，因为等同于增加固定电阻值，所以对零序电压、健全线路和故障线路零序电流分析同2.1 节。此情况下各线路对地电容参数的理论分析与结论也同样成立，不再赘述。

当电弧电阻R2为(k2+b/i)时，在过阻尼状态下故障线路n的出口零序电流i0n为衰减直流分量、工频稳态分量和非周期直流分量的叠加。

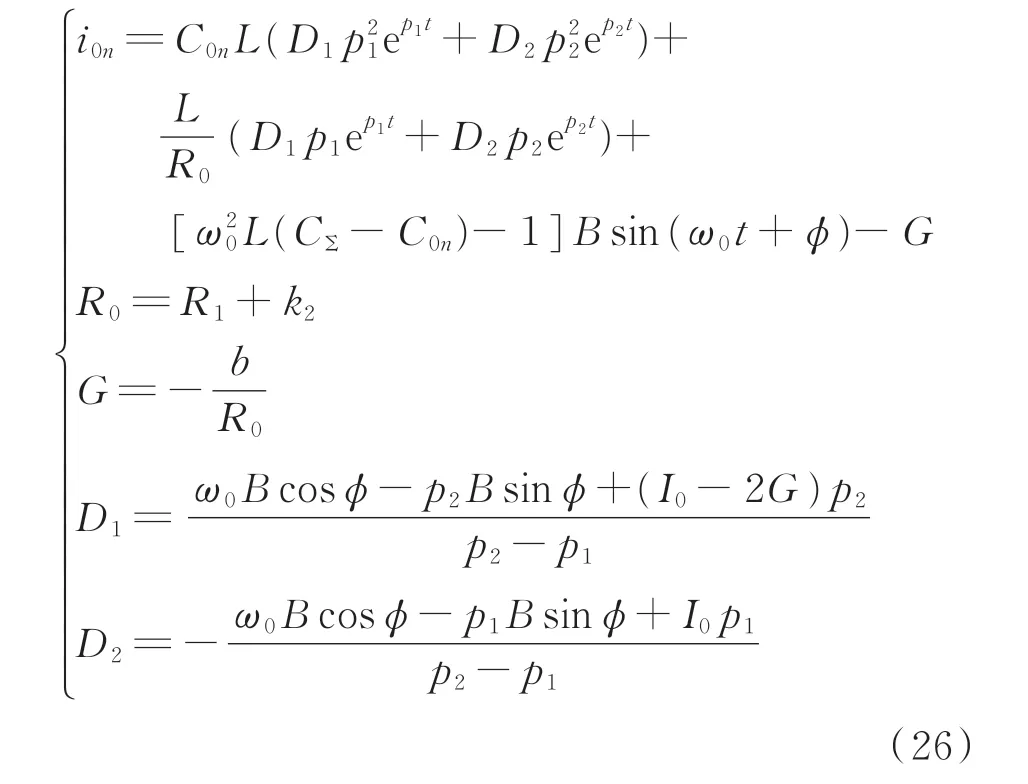
式中：R0、G、D1和D2均为中间变量；I0为故障线路零序电流有效值。

故障时刻系统暂态过程中故障线路对地电容参数仍满足：

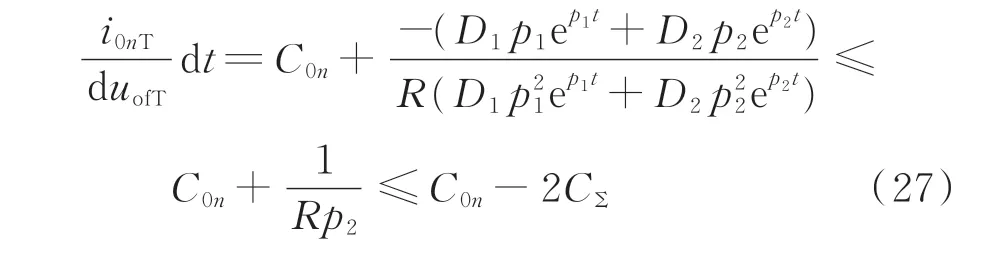
同理，在欠阻尼状态下故障线路的出口零序电流i0n为衰减交流分量、工频稳态分量和非周期直流分量的叠加。

式中：D3和D4均为中间变量。

经推导在故障初始时刻故障线路对地电容参数的变化也同样满足：

系统达到稳态时，由于故障线路零序电流带有直流分量，可推得其对地电容参数为：

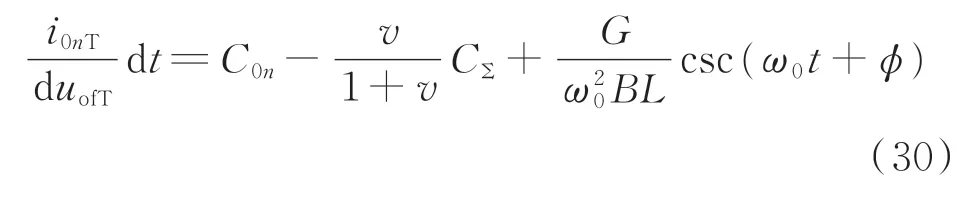
综上，引入电弧非线性等效电阻后，由于等效电阻增大，可能由原始的过阻尼状态过渡到欠阻尼状态，并且系统中的电气量幅值进一步降低。不论是过阻尼还是欠阻尼状态，引入电弧非线性电阻后，故障初始时刻故障线路对地电容参数下降的规律不变，并仍存在衰减过程。但是由式（30）可知，故障线路对地电容参数稳态表达式存在时变的函数，在暂态过程结束后始终无法达到稳态的某一固定值。

3 基于虚拟能量变化率的故障选线方法

3.1 高阻接地故障启动

传统的故障选线装置是通过检测系统零序电压有效值是否超过整定值来启动，若零序电压有效值越限则启动录波记录故障前后数据，一般整定值设为额定相电压幅值的15%。为消除三相不平衡的影响，且保证在故障初始角较小、故障电阻较大时故障启动的灵敏性，缩短启动时间，可利用零序电压相邻采样值之差定义突变能量［29］为：

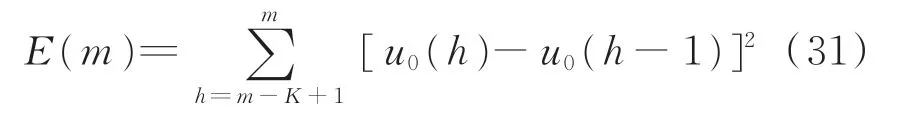
式中：u0(h)为母线零序电压的第h个采样点；K为一定时窗内的采样点数；m为当前采样点数，且m≥K。

考虑到系统中三相不同期合闸等瞬时干扰产生的零序电压可能造成误判，每半个工频周期计算突变能量的有效值，在适当降低灵敏性的基础上保证可靠性。在谐振接地系统设置三相不平衡的单相接地故障，过渡电阻分别为500 Ω 和3 kΩ，并取K=5。故障前后的突变能量值及其有效值如附录A 图A1和图A2 所示。

由图A1 和图A2 可见，未发生故障时三相不平衡系统中突变能量值也很小，接近于零，故障发生后其值快速增大，在故障电阻较小时可在故障后几毫秒立即启动，故障过渡电阻高至十几千欧时可在0.5～2 个工频周期内启动，可满足速动性要求。利用高阻故障发生时其零序电压由低到高的上升过程这一特征，判断故障发生后2 个工频周期内突变能量有效值是否出现下降，若每半个工频周期有效值未降低且逐渐增大，则判定为高阻接地故障。

3.2 虚拟能量变化率选线原理

根据2.1 节所述的故障时刻对地参数下降原理，在实际应用中选取适当的截止频率，利用惯性环节使故障线路n的对地电容参数在下降阶段的突变值大幅衰减，近似得到故障前即正常情况下的对地电容参数C′0n。利用C′0n求得线路n故障前的电流分量，与故障时刻后的零序电流作差，再与零序电压相乘构造表征线路n故障前后对地电容参数变化的虚拟能量。在系统高阻接地故障启动后，第j（j=1，2，…，n）条线路的虚拟能量可表示为：

式中：C′0j为第j条线路正常时的对地电容参数；i0jT为第j条线路的零序电流暂态分量；ΔC0j为第j条线路故障前与故障后的对地电容参数之差；Wvtj为第j条线路的虚拟能量。

到达稳态后由稳态量表达式求得线路出口的虚拟能量为：

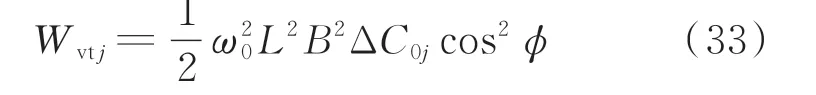
由于故障发生后暂态各阶段的ΔC0j与其变化率dΔC0j/dt大小关系的分析比较复杂，为便于判断，对虚拟能量表达式（32）进一步求导，得到虚拟能量变化率为：

式中：dWvtj/dt为第j条线路的虚拟能量变化率。因为零序电压暂态分量的平方始终大于零，所以dWvtj/dt与对地电容参数变化率dΔC0j/dt异号。

图3 为线路1 发生1.5 kΩ 接地故障后所有线路对地电容参数和虚拟能量变化率在各阶段的对比波形，图中虚线划分出的S0 到S5 为线路1 发生故障前后对地电容参数变化的各阶段，N1 到N3 为曲线上的特征点。表1 列出了故障线路1 各阶段对地电容参数变化量ΔC01、对地电容参数变化率dΔC01/dt以及虚拟能量变化率dWvt1/dt的符号变化。

表1 故障线路暂态过程各计算量符号Table 1 Signs of calculation quantities in transient process of line fault

由图3 所示，S0 阶段故障未发生，各计算量均为零。线路1 发生故障后随即进入暂态过渡过程，S1为对地电容参数C01的过渡下降阶段，线路1 的ΔC01单调递增，在N1 点达到最大值，dΔC01/dt为正，虚拟能量变化率为负；S2 和S3 为上升阶段，ΔC01逐渐减小，分别在N2 和N3 处减小至零和最小值，其变化率dΔC01/dt小于零，虚拟能量变化率为正，并且dWvt1/dt在此阶段内达到最大值；S4 为C01反向下降阶段，ΔC01由负值逐渐增大趋于稳定，其变化率dΔC01/dt大于零，虚拟能量变化率为负；S5 为稳态阶段，此时对地电容参数稳定至略大于故障前的参数值（消弧线圈过补偿），ΔC01稳定至负值，其变化率dΔC01/dt基本为零，虚拟能量变化率也为零。健全线路对地电容参数在故障前后基本没有变化，其对应的虚拟能量变化率幅值与故障线路相比大幅度减小，因此可以根据各线路虚拟能量变化率的正向峰值大小识别出故障线路。

图3 各线路对地电容参数和虚拟能量变化率波形对比Fig.3 Waveform comparison of line-to-ground capacitance parameters and virtual energy change rate of each line

根据上述原理，提出基于虚拟能量变化率的判据，在故障启动后计算出各条出线的虚拟能量变化率，并且求得各出线虚拟能量变化率正向峰值，判断虚拟能量变化率峰值占比最大且超过设定定值的线路为故障线路，其余线路为健全线路。

经2.2 节分析可知，高阻接地故障伴随的非线性电弧现象只是影响对地参数的稳态稳定性，而故障暂态过程仍符合对地电容参数下降规律，因此基于虚拟能量变化率的选线判据仍然适用。另外，可以通过差值运算去除故障前后均存在的线路对地不对称参数造成的固有零序分量的干扰，提升保护动作的可靠性。

3.3 故障选线流程

综合以上分析，提出基于对地电容参数下降原理和虚拟能量变化率判据的选线实现流程，具体包含以下5 个步骤。

步骤1：数字滤波。采集母线零序电压uof(m)及各线路零序电流i0j(m)，经由窄带数字滤波器滤除谐波。其中，j=1，2，…，n为线路号；m=1，2，…，M为采样点数，M为采样总点数。

步骤2：启动选线及故障录波。根据式（31）计算突变能量值E(m)，并每隔半个工频周期计算其有效值并判断是否越限且在2 个工频周期内递增。若未越限则保留当前工频周期电压电流数据，清除上一工频周期数据；若越限且递增则启动录波并执行步骤3。

步骤3：计算各线路的虚拟能量值。在工程上可将式（32）改写为下式，用于计算各线路虚拟能量：

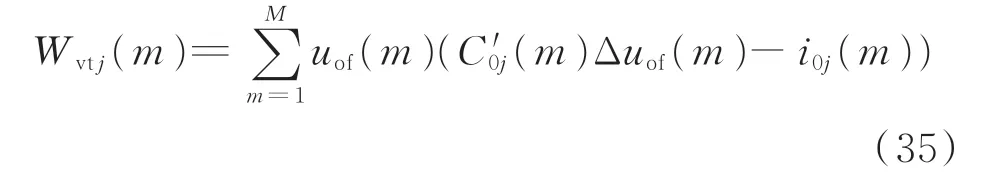
步骤4：根据各条线路的虚拟能量计算虚拟能量变化率ΔWvtj(m)及其正向峰值ΔWvt，max(j)。

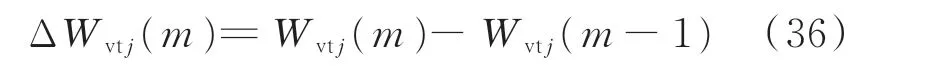
通过循环比较前后两个采样点的ΔWvtj(m) 和ΔWvtj(m+1)的值大小，取数值高的虚拟能量变化率不断赋值给ΔWvt，max(j)，最终求得整个故障持续时间内的正向峰值ΔWvt，max(j)。

步骤5：判断故障线路。求各线路虚拟能量变化率峰值占比：

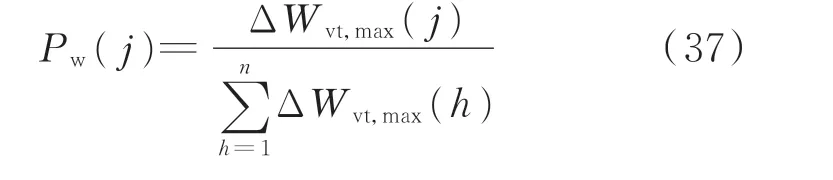
设定比例定值Pw，set，根据各线路计算出的虚拟能量变化率峰值占比Pw(j)逐条线路判断。若存在线路j的Pw(j)大于Pw，set，则判断线路j为故障线路。最后选线结束并发出命令切除故障。

在实际应用中考虑到测量设备的采集精度及系统三相不平衡，比例定值Pw，set不宜设置过小且最好留有10%的裕度。由于故障发生前电缆较长的健全线路的对地参数初值较大，这会导致求得的故障初期对地参数变化量波动较大，使故障线路峰值占比略有下降。可根据电缆比重与系统大小设定比例定值。对于出线不多或架空线比重大的系统，Pw，set可设为80%；对于电缆比重大的系统，Pw，set可设为60%～70%；出线较多的系统Pw，set可设为50%。

4 仿真验证

4.1 仿真模型及选线结果分析

利用电磁暂态仿真软件PSCAD 搭建10 kV 配电网谐振接地系统模型（见附录B 图B1），主变压器的额定容量100 MVA，系统电容电流为73.5 A，F1～F5 为不同的接地故障点。系统线路参数见附录B 表B1。

利用所搭建系统，取接地故障点F1 和F2 进行故障特征分析，系统消弧线圈的脱谐度v为-0.08；F1 处故障过渡电阻取2 kΩ，故障初始角为45°；F2 处故障过渡电阻取5 kΩ，故障初始角为90°。仿真得到的虚拟能量变化率波形图如图4 所示，零序电压、零序电流波形见附录B 图B2 和图B3。图B2 和图B3虚线框内区域为故障的暂态过渡过程，故障电阻越大，暂态过渡过程持续时间越长。由图4 可见，虚拟能量变化率在故障暂态过渡过程内才会变化，故障线路的波形变化各阶段均符合3.2 节分析，对应故障线路对地电容参数的下降、上升和反向下降阶段。随着故障电阻的增大，故障时零序电压、零序电流的幅值和虚拟能量变化率均变低，但是故障线路的虚拟能量变化率的波形趋势及幅值变化始终与健全线路有明显区分。在对地电容参数的上升阶段，故障线路的虚拟能量变化率存在峰值且明显高于其余健全线路，经计算故障线路的峰值占比分别为88%和84%，健全线路的峰值占比基本小于10%，由此可以准确选线。

图4 F1 和F2 处发生故障各线路虚拟能量变化率波形图Fig.4 Waveform diagram of virtual energy change rate of each line with faults at F1 and F2

4.2 高阻接地故障选线方法验证

对图B1 所示系统的F1～F5 处故障点分别以不同故障电阻和故障角进行仿真验证，列出各情况下各线路虚拟能量变化率峰值及最大占比，结果如表2 所示。

由表2 可知，在暂态过程中故障线路虚拟能量变化率的峰值占比始终最大且超过定值，而健全线路虚拟能量变化率的占比较小，本文所提出的选线算法可以准确识别故障线路。由仿真结果可见，在故障过渡电阻为20 kΩ 时故障线路峰值占比为71%，此系统可设置比例定值为60%，在此定值下本方法的耐高阻上限约为20 kΩ。

表2 不同故障情况下的选线仿真结果Table 2 Simulation results of line selection under different fault conditions

4.3 与暂态能量法的对比

在附录B 图B1 系统中引入三相不平衡（线路2三相对地参数不对称），在线路5 设置过渡电阻3 kΩ的接地故障，零序电流时域波形见附录B 图B4（a）。与图B4（b）三相平衡系统零序电流波形对比，三相不平衡较大的系统在发生故障后，不对称的线路2和故障线路零序电流突变方向均与其余健全线路相反，这会导致两条线路的暂态能量特征均与其余线路相反，难以选出故障线路。

利用文献［29］中的暂态能量法与本文所提方法做仿真对比，其结果如图5 所示。图5（a）中线路2和线路5 的暂态能量值均为负值，幅值大小也相近，利用暂态能量法的判据进行选线就会造成误判。暂态能量法对于2 kΩ 以下过渡电阻的故障具有较高的判断准确率，但是在过渡电阻较大且考虑系统三相不平衡干扰时，其判断会受到影响。而利用虚拟能量变化率峰值占比进行选线时，通过差值运算抑制对地不对称参数造成的故障前后均存在的固有零序分量干扰。在系统不平衡度范围内，不对称所在的线路2 的虚拟能量变化率会小幅增大，但是故障线路5 的虚拟能量变化率峰值占比仍达70%左右，可正确选出故障所在线路为线路5。

图5 暂态能量法与虚拟能量变化率法波形对比Fig.5 Waveform comparison between transient energy method and virtual energy change rate method

5 真型模拟系统验证

在国内某中低压配网真型模拟系统上进行多组单相接地实验，此系统包含3 条架空线路和4 条电缆线路，网架模型及参数如附录C 图C1 所示。实验过程中消弧线圈投入为过补偿。选取Ⅰ段线路1 和线路4 并分别设置单相接地故障点进行故障试验。故障类型包括经1 kΩ 和2 kΩ 电阻接地，利用实验数据验证基于虚拟能量变化率的选线算法的应用效果。

选取实验数据中4 组故障数据进行验证，各线路虚拟能量变化率峰值及其最大占比见附录C 表C1，其中两组波形见附录C 图C2 和图C3。虽然现场数据存在干扰，导致虚拟能量变化率存在波动现象，但仍可见在暂态过程中故障线路的虚拟能量变化率曲线变化幅度和正向峰值占比最大，具有与健全线路区别明显的故障特征。依据算法所提判据可以准确选出故障线路分别为线路1 和线路4，与现场实验选取的故障点位置相符。

6 结语

谐振接地系统发生高阻接地故障时故障量相对微弱且伴随非线性电弧现象，线路对地参数不对称所造成的零序分量对选线结果影响也较大，故障选线存在较大困难。高阻接地故障发生后，故障线路的对地电容参数会存在瞬时下降现象，高阻故障伴随的非线性电弧仅影响稳态过程而对参数下降规律没有影响，在此阶段故障线路对地电容参数的变化量会明显大于健全线路。本文基于此构造了反映故障前后系统对地电容参数变化量的虚拟能量，为了便于提取故障线路差异特征，提出利用各线路虚拟能量变化率峰值占比来确定故障线路的判据和方法，既能保证选出最大峰值所在线路，又可以避免在故障电阻升高、判断量数值降低时的误判。最后，仿真和现场模拟实验数据验证了此方法的准确性和可靠性。

本文方法适应大电阻接地故障检测且易于实现，可抑制三相对地参数不对称带来的固有零序分量影响，实际应用中受故障位置和初始角影响较小，有一定的抗干扰能力。此算法判据适用于出线不是很多的中小型系统，对于电缆线路较多的大型系统，所有健全线路虚拟能量变化率波动可能导致故障线路峰值占比减小，需要进一步研究和完善故障判据以适应多种运行工况。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。