磁耦合无线电能传输系统实本征态工作模式及能效特性分析

廖志娟，冯其凯，吴 凡，姜陈慧，夏晨阳

（中国矿业大学电气与动力工程学院，江苏省徐州市 221116）

0 引言

磁耦合无线电能传输（magnetic coupling wireless power transfer，MC-WPT）技术基于磁场耦合原理实现电能从电源端到用电设备端的无电气连接传输［1-3］，十分适用于移动、旋转等设备以及水下、煤矿等场合下的电气设备供电［4-7］，已经成为当下电气工程及自动化领域的研究热点。

目前，MC-WPT 系统常用工作模式主要有：一类是传统零相角模式，将副边回路的电路固有频率设置为系统的工作频率，通过调节原边的补偿电容，使得整个系统输入阻抗为纯阻性的工作模式［8-9］；另一类是2007 年美国麻省理工学院（MIT）提出的共振耦合模式（以下简称“MIT 磁共振模式”），将系统中各电路的固有频率设为相等，调整电源频率使得其等于各电路的固有频率的工作模式［10］。在某些系统拓扑及参数条件下，这两类工作模式相同。这两类工作模式可实现一定范围内高效传能，但传输距离或者传输方位一旦偏离最佳传能范围，系统的能效会急剧下降，甚至会随传输距离减小而减小［11-16］。文献［17-18］基于振动理论证实MC-WPT系统是一类由多个RLC 振荡电路通过磁场相互耦合而成的多自由度振荡系统，系统存在一系列复本征值，并提出了“复本征态”模式：系统的工作频率等于复本征值的模的工作模式。该模式可实现一定距离范围内最大功率传能，但工作频率需要随耦合系数变化而变化。

2017 年，Assawaworrarit 等人提出了“宇称时间（parity-time，PT）对称”的工作模式［19］，基于并联-并联型（parallel-parallel，PP）拓扑结构，采用运算放大器构建相应的负电阻以提供能量，在无需任何外部整定的情况下，可实现近1 m 范围内高效传能。该成果引起了国内外研究学者的广泛关注，后续相继提出了基于运算放大器实现的串联-串联型（seriesseries，SS）拓扑PT 对称系统［20］和基于逆变器实现的SS 拓扑PT 对称系统［20-25］。

目前，基于运算放大器实现的SS 拓扑PT 对称系统的相关研究较少。文献［20］给出了基于运算放大器实现的SS 拓扑PT 对称系统的原理图，但系统实现及验证都是基于逆变器实现的，该文并未对这两种实现方式的本质区别进行分析。同时，笔者实验室大量仿真和实验结果表明，直接将文献［19］中的运算放大器应用到SS 拓扑结构中，系统难以稳定运行。目前还未见有文献揭示PT 对称系统不同实现方式之间的本质差异，而物理原理揭示是跳出拓扑结构及参数优化，进行更深层次模式创新的基础。

基于逆变器实现的PT 对称系统，是目前的研究热点［20-25］，但大多数研究都是在该工作模式上对系统的结构进行改变或对系统的参数进行优化，例如，文献［20］将两线圈PT 对称系统推广到多负载结构中，文献［24］将PT 对称系统的恒功率恒效率特性应用到物流机器人全向充电系统中，文献［25］在接收电路中增加了一个电感来拓宽PT 对称区域等。由于基于逆变器实现的PT 对称系统和传统复本征态模式一样，需要随耦合系数变化不断地调整逆变器的频率，而两者之间的本质区别目前认识并不全面。构建PT 对称系统的一般数理描述，从物理原理上揭示其与传统各工作模式之间的联系与区别，可为实际系统优化设计及工作模式的选择提供相应的理论指导，同时理清工作模式，便于后续创新。

针对上述问题，鉴于3 个方面原因（1）在量子理论中，PT 对称系统哈密顿量的本征值为实数［26］；2）一个物理系统的本征参数能够完全表征系统的内在物理原理及外部特性，同时也是基于电参数描述，易于电气工程师理解，便于指导实际系统设计；3）基于本征态建模，能够和已有的工作模式，包括MIT 磁共振模式、复本征态模式构建统一的数学模型，便于对比分析），本文将基于振动理论，从本征态角度对PT 对称系统进行建模分析，以此揭示PT 对称系统的物理原理，构建不同工作模式的数理描述，区分工作模式之间的原理及能效差异，为实际系统设计以及工作模式的选择提供理论依据。本文以SS 拓扑结构为例，但揭示的物理原理及分析方法同样适用于PP 拓扑结构。

1 理论分析

1.1 实本征态系统建模

PT 对称MC-WPT 系统的一般等效电路如图1所示，其中：负电阻Rg为供能元件；Rp1、L1、C1和Rp2、L2、C2分别为发射线圈和接收线圈的等效串联电阻、线圈自感和谐振补偿电容；i1和i2分别为发射线圈和接收线圈的电流；u1和u2分别为补偿电容C1和C2两端的电压；M为两线圈间的互感；RL为负载电阻。

图1 PT 对称MC-WPT 系统等效电路图Fig.1 Equivalent circuit diagram of PT-symmetric MCWPT system

根据基尔霍夫电压定律，图1 所示系统的数学模型可表示为：

式（2）为典型的二阶齐次微分方程，其解可表示为U=U0ejλt，其中U0为常 数向量，λ=jδ±ω为系统的本征值。本征值虚部δ表征系统的衰减特性，实部ω为系统自由响应的振荡频率。当δ＞0 时，系统响应为衰减振荡；当δ＜0 时，系统响应为发散振荡；当δ=0 时，系统响应为等幅振荡。对于不存在外部激励的自由响应系统而言，无论自由响应是发散振荡还是衰减振荡，系统都是不稳定的。当且仅当自由响应为等幅振荡时，即δ等于零时，系统才能稳定运行。

为了便于后续分析，将系统本征值为实数（即虚部δ=0，本征值为λ=±ω）的状态称之为“实本征态”。图1 所示的MC-WPT 系统只能在实本征态模式下稳定运行。因此，PT 对称MC-WPT 系统实质就是工作在实本征态模式。

1.2 实本征态系统参数条件

本节将深入分析实本征态MC-WPT 系统的一般参数条件，为实本征态系统设计提供相应的理论准则。

将U=U0ejλt代 入 式（2），可 得 系 统 的 本 征 方程为：

式中：

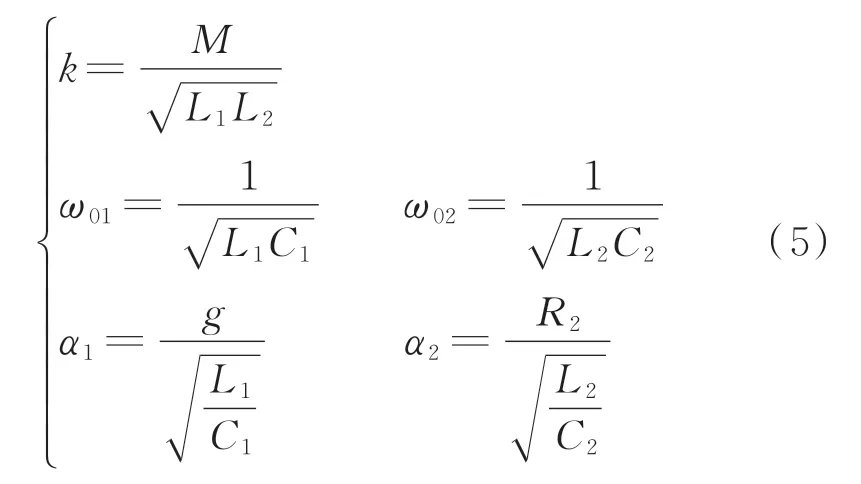
式中：k为两线圈之间的耦合系数；ω01和ω02为两线圈的固有谐振频率。

对MC-WPT 系统而言，不失一般性，可令L1=L2=L，C1=C2=C，将其代入式（5），可得ω01=ω02。令ω01=ω02=ω0，将其及实本征态模式的本征值条件λ=±ω代入式（4），可得实本征态系统的特征方程可表示为：

求解式（6），可得实本征态MC-WPT 系统的参数条件分别如式（7）和式（8）两组解所示。

0 ＜k＜1 时，有：

由上述分析可得，振荡频率ω及负电阻总阻值g随耦合系数k变化曲线，如附录A 图A1 所示。当耦合系数k＜k1时，有且仅有定频实本征态一种工作模式；当耦合系数k＞k1时，系统同时存在定频实本征态和浮频实本征态两种工作模式。定频实本征态振荡频率恒定在ω=ω0，g=k2ρ20/R2会随着k增大而增大。而浮频实本征态的负电阻总阻值恒定在g=R2，振荡频率ω=ω1，2随着k变化而变化。两种工作模式在耦合系数k=k2=α2处相交。

1.3 实本征态系统的阻抗特性

基于电路等效变换，图1 所示的MC-WPT 系统除负电阻以外的电路都可等效为一个RLC 电路，如附录A 图A2 所示。当电路工作频率为ω时，等效电阻Req和等效电抗Xeq=ωLeq-1/（ωCeq）如下：

定频实本征态模式下，有：

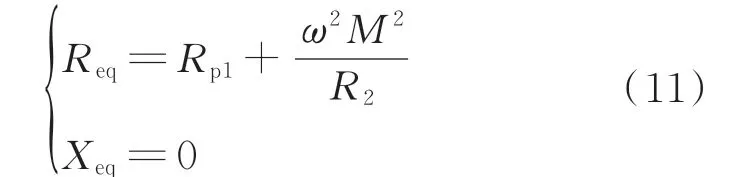
浮频实本征态模式下，有：

定频实本征态模式输入阻抗的值随互感（耦合系数）增大而增大，浮频实本征态模式输入阻抗的值与耦合系数无关。

2 实本征态系统的实现及特性分析

2.1 基于运算放大器实现的实本征态系统分析

基于运算放大器来构建负电阻是目前常用的方法［19-20］，但其工作机制及物理原理目前认识并不全面，基于量子理论的分析对于电气工程师来说也难以理解，因此本节将从电路理论入手，给出基于运算放大器实现的负电阻电路，进而分析其工作原理及能效特性。

2.1.1 电路拓扑及工作原理

基于运算放大器实现的MC-WPT 系统等效电路如图2 所示［19-20］。根据运算放大器电路的虚短及虚断特性，左侧蓝色方框内的运算放大器电路的端口特性可等效为一个阻值为-Rg的负电阻。

图2 基于运算放大器实现的MC-WPT 系统等效电路图Fig.2 Equivalent circuit diagram of MC-WPT system based on operational amplifier

由式（11）和式（12）可知，PT 对称MC-WPT 系统的输入阻抗为纯阻性。因此，图2 所示的基于运算放大器实现的MC-WPT 系统可等效为图3（a）所示的电路图，相应的方框原理图如图3（b）所示，其中：ui为 输 入 电 压；uo为 输 出 电 压；uf为 反 馈 电 压；A=uo/ui表示放大倍数，F=uf/uo表示反馈系数，具体表达式如式（13）所示。

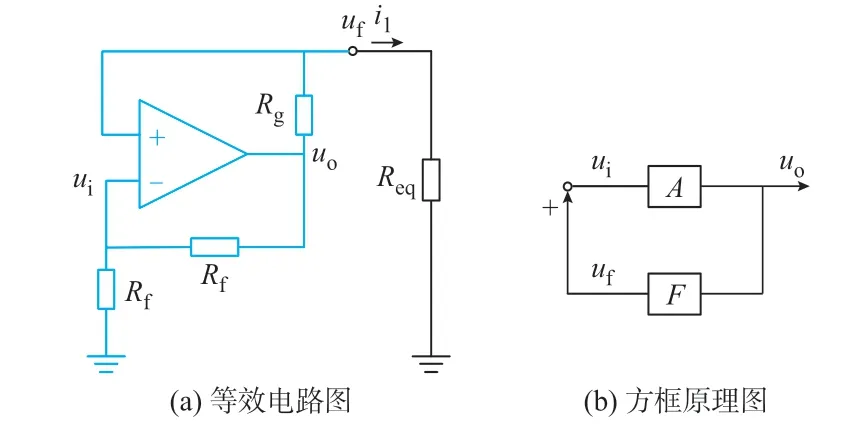
图3 基于运算放大器实现的实本征态系统等效电路图及方框原理图Fig.3 Equivalent circuit diagram and block schematic diagram of real eigenstate system based on operational amplifier

对于定频实本征态模式，有g=ρ20k2/R2，Req=Rp1+ω2M2/R2。联立g=Rg-Rp1以及式（13），可得AF=1。对于浮频实本征态模式，有g=R2，Req=Rp1+R2，联立g=Rg-Rp1以及式（13），可得AF=1。可知，无论是定频实本征态还是浮频实本征态，都有放大倍数A以及反馈系数F的乘积为1。同时基于式（13）可知，无论是定频实本征态还是浮频实本征态模式，输入阻抗总为纯阻性，反馈电压uf和输出电压uo同相位。该分析结果表明，实本征态MC-WPT系统的工作原理实质上就是自激振荡系统，系统响应为自由响应。MC-WPT 系统的磁耦合机构、谐振拓扑以及负载组成选频网络。在特定的频率下，反馈电压uf和输出电压uo同相位，满足正反馈条件，相应的频率信号就会被选出，因此系统具有自选频功能。

无论是SS 拓扑结构还是PP 拓扑结构，无线电能传输系统都只是选频网络，只对选出的频率值有影响，对系统的工作原理没有任何影响。因此上述工作原理的分析同样适用于PP 拓扑结构。

2.1.2 能效特性分析

对于图2 所示的基于运算放大器实现的MCWPT 系统，基于相量运算，系统数学模型为：

只考虑运算放大器电路右侧MC-WPT 系统的能效特性时，系统的传输效率η和传输功率Pout为：

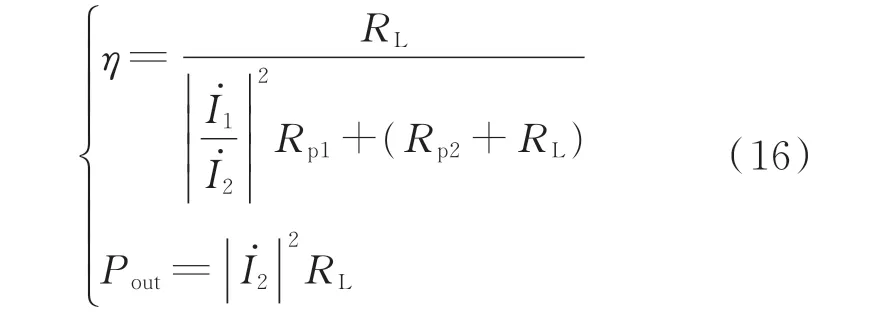
将式（15）求得的电流关系代入式（16），可得实本征态系统的传输效率为：

式（17）表明，对于定频实本征态模式，系统的传输效率会随耦合系数（互感）减小而减小。而对于浮频实本征态模式，传输效率和耦合系数无关。并且由于线圈内阻Rp1和Rp2通常都很小，由式（17）可知，浮频实本征态模式的传输效率通常非常高，该分析结果表明，浮频实本征态模式的传输效率在一定传输距离范围内恒定在一个较高的值。

尽管基于运算放大器实现的浮频实本征态系统能够在一定范围内实现高效传能，但由于运算放大器内部损耗很大，因此系统的整体效率并不高。同时，由于运算放大器的输出电流很小，系统的输出功率也非常小。更关键的是，对于图2 所示的基于运算放大器实现的SS 拓扑的浮频实本征态系统，虽然在理论上满足自激振荡特性，但是由于虚拟极点的存在，无法实现稳定的自激振荡［23］。

2.2 基于逆变器实现的实本征态系统分析

为了提升系统的整体效率，文献［21］通过控制逆变器的频率，使得逆变器的输出电压与输出电流相位相同，构建了基于逆变器实现的PT 对称MCWPT 系统，而基于逆变器实现的实本征态模式与常用工作模式的差异目前认识并不全面。本节将对基于逆变器实现的实本征态系统工作原理及系统特性进行分析。

2.2.1 电路拓扑及工作原理

基于逆变器实现的MC-WPT 系统原理图如图4 所示，由直流电压源与H 桥逆变器共同构成外部交流激励源。

图4 基于逆变器实现的电路原理图Fig.4 Schematic diagram of inverter-based circuit

对于如图4 所示的全桥逆变器，直流电压为VD。当开关频率为ω，对应的周期为T时，逆变器的输出电压Vin1将是周期为T、幅值为VD的正负方波，相应的表达式为：

式中：N为正整数。

基于基尔霍夫电压定律，可得图4 所示系统的数学模型为：

对比式（19）和式（1）可知，当且仅当电源电压外特性等于图1 所示的负电阻时，即Vin1/(-i1)=-Rg时，基于逆变器实现的PT 对称系统的数学模型为齐次方程，和基于运算放大器实现的PT 对称系统数学模型一致，为实本征态模式。但是由式（18）可知，逆变器输出电压Vin1为方波。在式（7）及式（8）所示频率下，输入侧电流i1为正弦波，因此逆变器的外特性严格意义上都不会等于图1 所示的负电阻。只有基于基波近似等效，即式（18）所示的方波等效为式（20）所示的正弦电压源Vin2时，Vin2和一次侧电流i1同相位，其外部特性Vin2/(-i1)=-Zin可等效为图1 所示的负电阻。

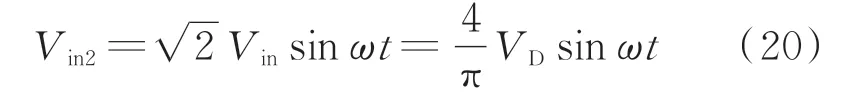
式中：Vin为等效正弦电压源的有效值。

只有在基波近似等效的前提下，式（7）及式（8）所示工作频率下的逆变器外特性才可以等效为负电阻，系统的数学模型和基于运算放大器实现的PT对称系统的数学模型一致，为齐次方程，系统的响应可以看成自由振荡。但一方面，逆变器的输出波形为方波，在给定的频率下，逆变器的外特性严格意义上并不等于负电阻。更重要的是，基于逆变器实现的PT 对称系统的工作频率是由逆变器的开关管频率决定的，并不是由系统本身的选频网络选择的，逆变器的开关频率调节到其他频率点，系统也能稳定工作。同时，基于逆变器实现的PT 对称系统没有放大环节，也没有正反馈环节。因此，把逆变器及其开关频率调节电路看作外部激励更为合适。基于此，本文将基于逆变器实现的PT 对称系统响应归类为强迫响应，和传统工作模式一样。

2.2.2 能效特性分析

对于图4 所示的MC-WPT 系统，基于基波近似等效法，系统传输效率η和输出功率Pout的表达式仍如式（16）所示。对于定频实本征态模式，逆变器的开关频率为ω=ω0，此时Req=Rp1+ω2M2/R2，为纯阻性。该分析表明，基于逆变器实现的定频实本征态模式和传统的MIT 磁共振模式一样，同时也是传统的零相角模式。定频实本征态模式的能效表达式如下：

传输效率随耦合系数（互感）减小而减小，传输功率随耦合系数减小先增大后减小，功率存在频率分裂现象。

对于浮频实本征态模式，逆变器的开关频率为ω=ω1，2，此时Req=Rp1+R2，即浮频实本征态系统也属于零相角频率，但该频率与传统的零相角模式的频率并不相同。浮频实本征态模式下系统的能效如下：

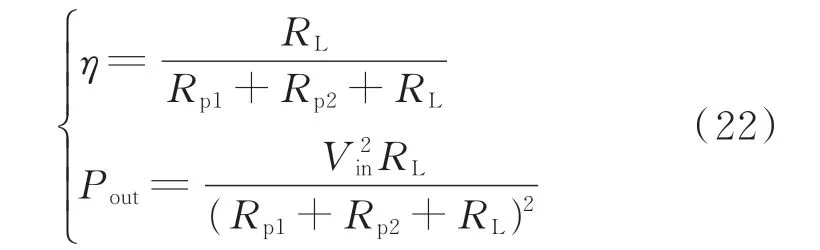
传输效率和输出功率都和耦合系数无关。同时，由于线圈内阻Rp1和Rp2一般都很小，因此系统的传输效率和传输功率都很大，即传输效率和输出功率可在一定传输距离范围内恒定在很大的值。

3 不同工作模式物理原理及特性分析

本章首先对第2 章提到的实本征态系统的两种实现方式进行对比，然后将实本征态模式与目前常用的工作模式进行对比，从物理原理及能效特性两方面给出MC-WPT 系统各个工作模式之间的联系与区别。

3.1 基于运算放大器和基于逆变器实现的实本征态系统对比分析

基于第2 章的理论分析，可以得出基于运算放大器和基于逆变器实现的实本征态系统存在以下几点区别及联系：

1）从物理原理及电路响应的角度来看，基于运算放大器和基于逆变器实现的实本征态系统的本质是不一样的。基于运算放大器实现的实本征态系统实质为自激振荡，工作频率由系统自身的选频网络决定，系统响应属于自由响应。当且仅当系统响应为等幅振荡时，系统才能稳定运行。而基于逆变器实现的实本征态系统，由于外接了激励源，系统做强迫振荡，系统响应=自由响应分量+强迫响应分量。对于实际系统而言，由于阻尼的存在，自由分量一般为衰减振荡，系统的本征值一般为复数。只有在某些特定频率下，基于基波近似等效法，将逆变器与电源等效为一个负电阻元件代入特征方程，才能使得系统的本征值为实数。但从根本上来说，逆变器与电源的组合为系统的外部激励，基于逆变器实现的PT 对称系统做强迫响应。两者的物理原理是不一样的。

2）从系统能效特性角度来看，对比式（17）、式（21）和式（22）可知，基于运算放大器和基于逆变器实现的实本征态系统的传输效率是完全一致的，但是基于运算放大器实现的系统整体效率小于基于逆变器实现的系统的整体效率。输出功率方面，由于运算放大器输出电流很小导致基于运算放大器实现的系统输出功率较小，而基于逆变器实现的系统通过调节直流电压源的大小可以实现输出功率远大于前者。

3）当电路各部分元件参数都确定好后，基于运算放大器实现的系统仅适合工作在浮频实本征态模式，而基于逆变器实现的系统在两种工作模式下均可运行。这主要是由于：在基于运算放大器实现的系统中，定频实本征态模式下系统的输入阻抗会随耦合系数增大而增大，为了满足自激振荡条件AF=1，系统的负电阻总阻值也需要随耦合系数变化进行在线调整，但是对于图2 所示的负电阻的电路，当确定好电路参数后负电阻阻值就无法再改变，也就是系统只能工作在特定距离下。而浮频实本征态模式下系统的输入阻抗与耦合系数无关，一旦系统的负载给定，系统的负电阻总阻值也为定值，不随耦合系数改变而变化，因此当传输距离变化时，系统可以稳定工作在浮频实本征态模式下。在基于逆变器的系统中，当耦合系数及对应的工作频率改变时，等效负电阻总阻值自动随系统输入阻抗的变化而变化，因此只要调整外部激励频率，系统既可以工作在浮频实本征态模式，也可以工作在定频实本征态模式下。

3.2 MC-WPT 常用工作模式特性对比分析

本节将对比分析基于逆变器实现的实本征态工作模式和传统的基于逆变器实现的工作模式（包括传统零相角模式、MIT 磁共振模式和复本征态模式），以区别不同工作模式下的能效特性及特点。

根据引言中的定义可知，传统零相角模式将副边回路的电路固有频率设置为系统的工作频率，通过调节原边的补偿电容，使得整个系统输入阻抗为纯阻性的工作模式［8-9］。对于SS 拓扑两线圈结构，该模式下的两个电路固有频率相等，工作频率等于两个电路的固有频率。但对于其他拓扑结构，比如串 联-并 联 型（series-parallel，SP）、并 联-串 联 型（parallel-series，PS）等，各电路的固有频率就不再相等，工作频率只等于副边回路的电路固有频率；MIT 磁共振模式是指将所有回路的电路固有频率设为相同，调节逆变器的开关频率使得其等于设置的电路固有频率的工作模式［10］。对于SS 拓扑两线圈结构MC-WPT 系统而言，系统的输入阻抗为纯阻性，系统具有零相角特性。但是对于多线圈架构MC-WPT 系统，非相邻线圈间的交叉耦合会使得系统的输入阻抗不为纯阻性，系统不具备零相角特性；复本征态模式指的是系统外部激励频率等于系统本征值的模的工作模式，此时整个系统处于共振状态，输出功率较大。在耦合系数较小时，系统本征频率的模和电路固有频率特别接近，此时MIT 磁共振模式和复本征态模式相同。但在强耦合区域，存在频率分裂，MIT 磁共振模式不是物理意义上的共振，系统的输出功率很小［17-18］。该分析结果表明，对于SS 拓扑两线圈结构MC-WPT 系统而言，定频实本征态模式、MIT 磁共振模式以及传统的零相角模式相同，均为ω=ω0的模式，因此后续对比分析中，将这3 种工作模式统一归为传统工作模式。

为了对不同工作模式下的特性进行对比分析，结合图4 所示的电路拓扑以及附录A 表A1 所示的电路参数，应用式（7）、式（8）、式（21）、式（22）以及文献［9］中各个工作模式下的工作频率及能效公式，可得传统工作模式（MIT 磁共振模式、传统零相角模式、定频实本征态）、浮频实本征态和复本征态3 种工作模式下系统的工作频率、传输效率及传输功率随耦合系数的变化曲线，如图5 所示。

由图5（a）可知，传统工作模式的工作频率等于系统固有谐振频率，与耦合系数无关，浮频实本征态模式的有效工作范围为奇异点右侧，其工作频率偏离系统固有谐振频率，复本征态模式的工作频率在耦合系数较小时接近系统固有谐振频率，在耦合系数较大时偏离系统固有谐振频率。

由图5（b）可知，传统工作模式与复本征态模式的传输效率随耦合系数的增大而增大，浮频实本征态模式在奇异点右侧保持恒定的传输效率。

由图5（c）可知，传统工作模式与复本征态模式的输出功率随耦合系数的增大先增大后减小，功率曲线存在峰值点，这是由于模态重叠导致的。浮频实本征态模式在奇异点右侧保持恒定的输出功率，且两组工作频率ω1，2的系统能效完全一致，复本征态模式下两组工作频率ω3，4的系统能效不完全相同，但差别很小。

图5 不同工作模式下系统特性的仿真结果Fig.5 Simulation results of system characteristics in different operating modes

对于具体的系统能效特性而言，传统工作模式保持恒定的工作频率，系统的传输效率为3 种工作模式下最大，但是系统输出功率在耦合系数较大时非常低，存在频率分裂现象，因此适用于对传输效率要求较高的小功率系统。浮频实本征态模式与复本征态模式的工作频率都随耦合系数改变而改变，两种工作模式下的传输效率和输出功率都比较高，在耦合系数较大时两者差别很小。这两种工作模式的区别在于，浮频实本征态模式的有效工作范围受奇异点影响，在有效工作范围内具有恒功率恒效率的特性，与传输距离无关；复本征态模式不受奇异点的限制，有效工作范围更大一些，但是不具有能效恒定这一特性。在实际应用中，可以根据实际需求选择一种合适的工作模式。

根据前面揭示的物理原理以及分析的不同工作模式的特性，可以得到如表1 所示的各种工作模式的性能对比。根据表1 可以清晰地知道各种工作模式的区别与联系，从而可有效指导实际系统优化设计及工作模式的选择。

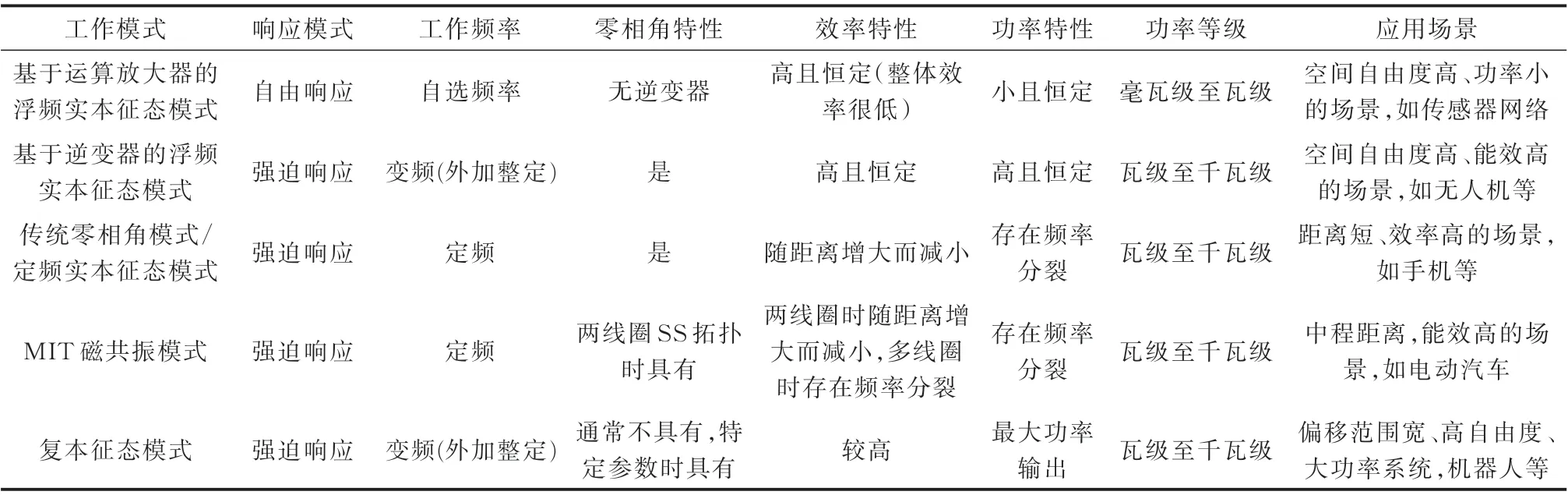
表1 不同工作模式的系统性能对比Table 1 Comparison of system performance in different operating modes

4 实验验证

为了验证上述分析的正确性，搭建了如附录A图A3 所示的实验装置。实验系统包括信号发生器、现场可编程逻辑门阵列（FPGA）、全桥逆变器、发射线圈、接收线圈和负载，相应的元件参数以及线圈的几何参数如附录A 表A1 和表A2 所示，其中逆变器内阻是根据笔者课题组前期大量的实验得到的该工况下的经验值。

4.1 实本征态系统阻抗特性验证

根据1.3 节的理论分析可知，无论是定频实本征态还是浮频实本征态模式，系统的输入阻抗均为纯阻性，即逆变器输出电压Vin1与一次侧电流i1同相位。定频实本征态模式的发射端和接收端电流相位相差90°，浮频实本征态模式的发射端和接收端电流幅值相等。为了验证上述分析的正确性，选取系统传输距离为24 cm，对应系统耦合系数为k=0.092 5，分别测量两种工作模式下系统的逆变器输出电压、发射端电流和接收端电流的波形，实验结果如图6 所示。

如图6（a）和（b）所示，无论是定频实本征态模式还是浮频实本征态模式，逆变器输出电压Vin1与一次侧电流i1同相位。由此可证实，基于基波近似等效法，逆变器的外部特性可以等效为负电阻。此外，从图6（a）可以看出，定频实本征态模式下，i1有效值为486 mA，i2有效值为964 mA，两个回路的电流幅值并不相等，不存在明确的幅值关系，但是相位刚好相差90°。浮频实本征态模式下，从图6（b）可以看出，i1有效值为1.76 A，i2有效值为1.78 A，两个电流幅值近似相等。但此时没有明确的相位关系。实验结果与理论分析结果一致。

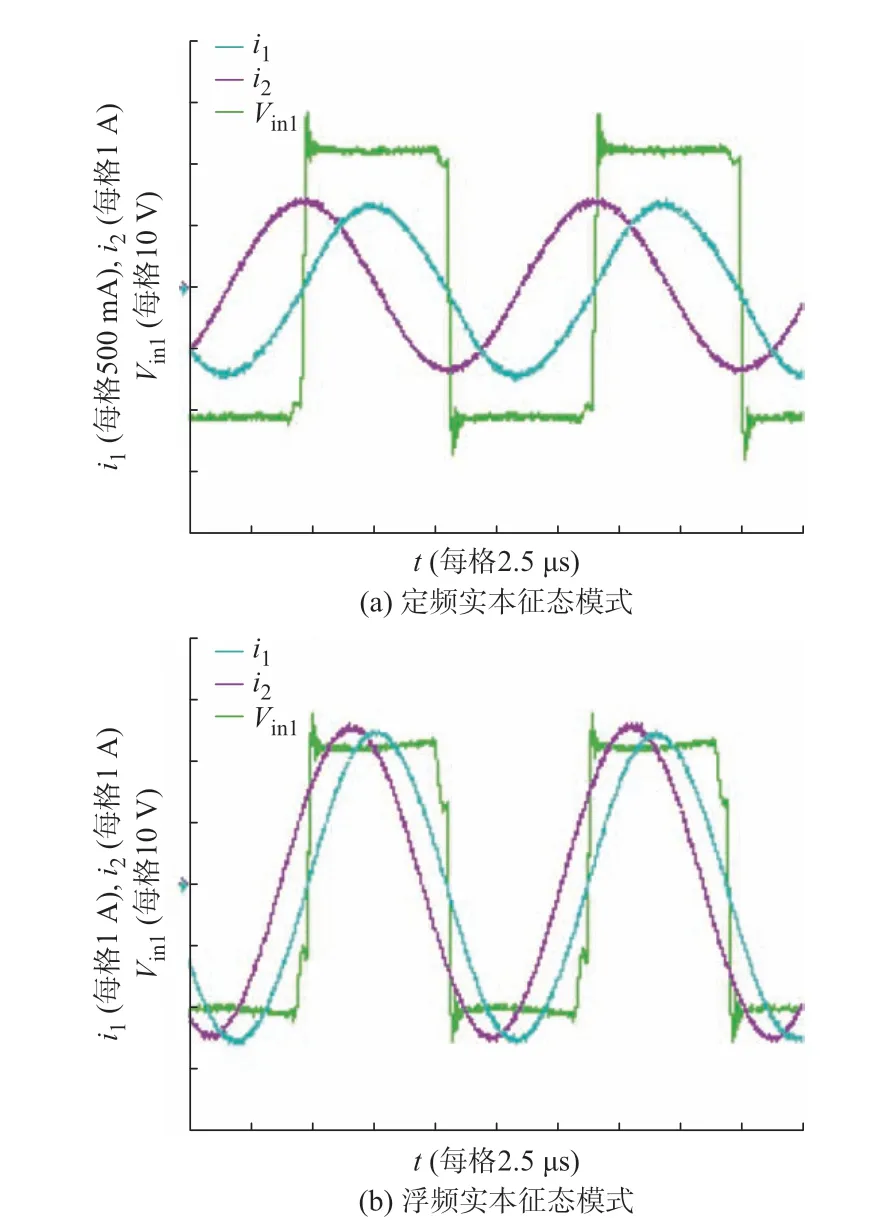
图6 不同工作模式下的系统特性曲线Fig.6 Characteristic curve of system in different operating modes

4.2 不同工作模式下的能效特性验证

本节分别对基于逆变器方式的传统工作模式（MIT 磁共振模式、传统零相角模式、定频实本征态）、浮频实本征态模式和复本征态模式的能效特性进行实验验证。基于附录A 表A1 所给电路参数，可得k1=0.048 5，对应传输距离为30 cm，即浮频实本征态模式只能在0～30 cm 之间工作，而其他工作模式不受此限制。在本组实验中，系统的传输距离以2 cm 的步长从6 cm 变化到40 cm。不同传输距离下各种工作模式的频率如图7 所示。基于图7 所给出的不同工作模式对应的频率，实验可得不同工作模式下系统的传输效率和输出功率随传输距离的变化曲线，如图8（a）和（b）所示。在图8 中，实线表示的是以传输距离为横坐标的系统能效仿真结果，该部分与图5 中以耦合系数为横坐标的仿真一一对应，虚线表示实验测量结果。

图7 不同传输距离下各种工作模式的频率Fig.7 Frequency of operating modes at different transfer distances

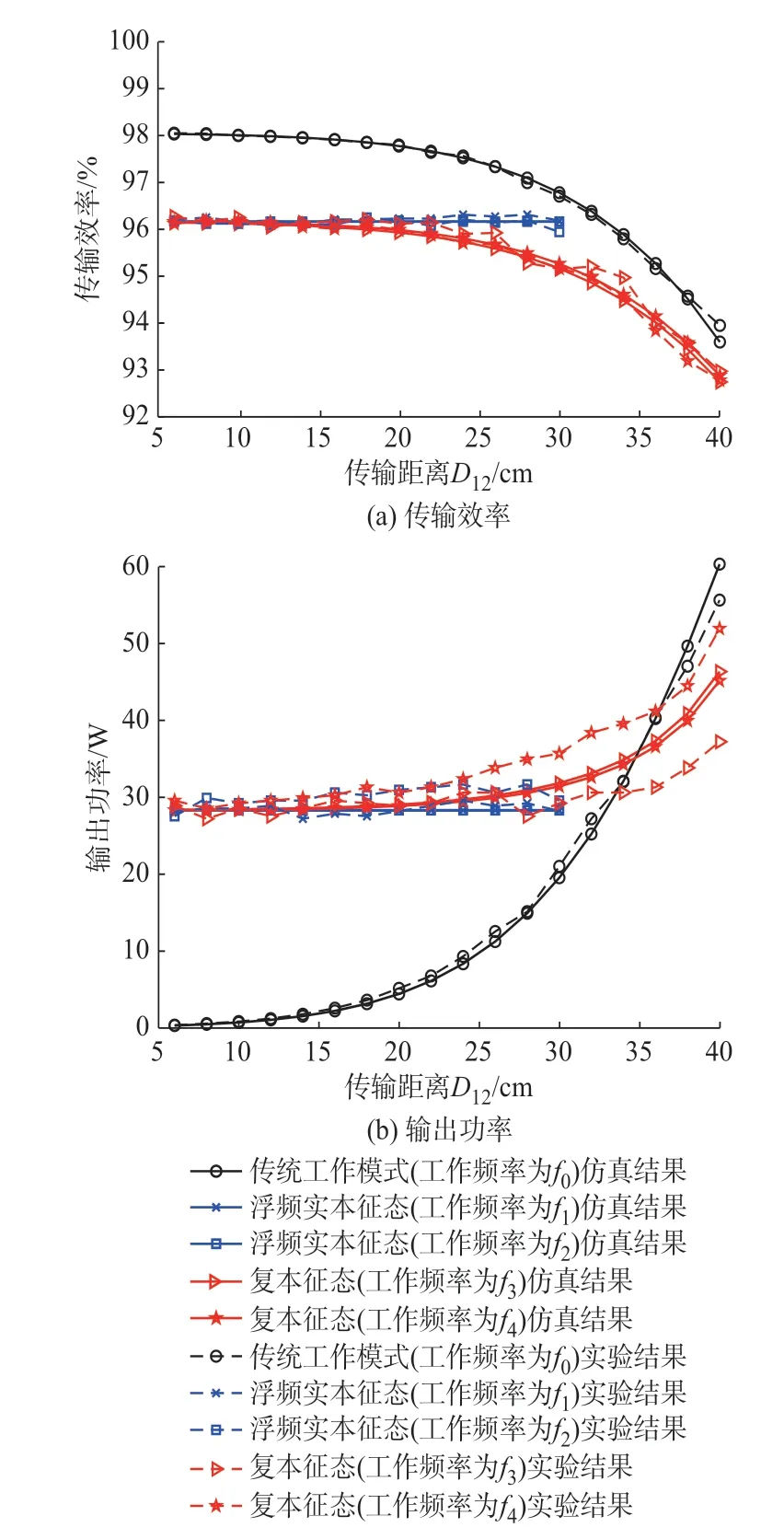
图8 不同工作模式下系统能效的实验结果Fig.8 Experimental results of system energy efficiency in different operating modes

由图8 可知，传统工作模式的传输效率最高，但是输出功率在近距离时非常低。浮频实本征态模式有效工作范围受奇异点的限制，在有效工作范围内传输效率和输出功率均较高且保持恒定。复本征态模式的传输效率和输出功率均较高，有效工作范围更大，但不具有能效恒定这一特性。实验结果与仿真结果基本吻合，由于系统参数误差以及实验测量误差，实验结果存在部分偏差。

5 结语

本文基于振动学理论，对PT 对称MC-WPT 系统进行建模分析，证实其实质为实本征态工作模式，并构建了实本征态系统的一般参数条件，同时揭示了基于运算放大器实现和基于逆变器实现的PT 对称系统的物理原理，并和传统常用的工作模式进行了对比分析。本文的主要创新工作如下：

1）针对目前PT 对称系统缺乏工作模式及电参数之间数理描述的问题，基于振动理论分析，明确PT 对称系统实质是工作在实本征态，进而构建得到了实本征态系统的一般参数条件，并证实定频实本征态与浮频实本征态的输入阻抗均为纯阻性，浮频实本征态模式在一定传输距离内具有恒定的输出功率和恒定的传输效率。本文构建的参数准则及系统特性能够有效指导实际系统参数设计。

2）针对PT 对称系统物理原理认识不全面、电气工程师难以理解的问题，基于PT 对称系统的电路特性，证实：基于运算放大器实现的PT 对称MCWPT 系统，其物理原理是自激振荡系统，因而具有自选频率特性，系统响应属于自由响应；而基于逆变器实现的PT 对称系统属于强迫响应，工作频率由逆变器决定。本文揭示的物理原理能够有效指导PT 对称特性应用到其他拓扑架构系统中。

3）针对目前MC-WPT 系统工作模式众多，但各工作模式之间的差异认识不全面的问题，从物理原理、能效特性等方面对目前常用的强迫响应工作模式进行了对比分析，证实：传统工作模式（MIT 磁共振模式、传统零相角模式、定频实本征态模式）的传输效率最高，但是输出功率在近距离时非常低；浮频实本征态模式的有效工作范围受奇异点的限制，在有效工作范围内系统传输效率和输出功率均较高且保持恒定，与传输距离无关；复本征态模式的传输效率和输出功率均较高，有效工作范围更大，但不具有恒定能效这一特性。本文总结的各种工作模式的能效特性及优缺点为实际系统工作模式的选择提供了理论依据。

基于运算放大器实现的PT 对称系统，由于虚拟极点的存在，难以应用到SS 拓扑结构中。后续可基于本文揭示的自激振荡原理，研究基于运算放大器实现的不同拓扑PT 对称系统。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。