基于电压折射波幅值正负差异的柔性直流电网两段式行波保护

陈田田，李银红

（强电磁工程与新技术国家重点实验室，华中科技大学，湖北省武汉市 430074）

0 引言

面对以发展可再生清洁能源为方向的能源结构调整，基于化石能源的传统交流电网难以大规模、远距离地接纳这些新能源，必须寻求新的输电技术。得益于电力电子技术的发展，柔性直流电网成为了解决这类问题的有效手段之一［1-4］。

目前，柔性直流电网常采用架空输电线路，线路故障发生概率高［5-7］。由于柔性直流电网是低惯性网络，故障电流上升速度快、幅值大，若不及时清除故障换流器将闭锁，因此对线路保护速动性提出了很高的要求，一般要求保护出口时间在3 ms 内［8-10］。如何快速准确地识别和切除故障，是发展柔性直流电网亟须解决的一大问题。

行波保护是一种可以快速动作的保护方案，在常规直流系统中作为主保护得到了广泛应用［11-12］。然而，传统行波保护虽然满足了速动性的要求，但耐受过渡电阻能力差，选择性和可靠性不足［8］。柔性直流电网线路故障时，各个换流站均向故障点馈入电流，仅依靠传统行波保护更难以准确识别故障位置［13］。

为提高行波保护在线路中的保护性能，国内外学者做了许多改进研究。文献［14］结合电流变化率判据，通过绘制电压变化率和电压变化量的轨迹确定行波保护区，但降低了过渡电阻的影响。文献［15-16］通过分析环网中正、反向故障行波的传播特性，利用行波幅值积分或突变能量构造判据，有较强的抗过渡电阻能力，但需要两端通信，牺牲了一定的速动性。文献［17-18］基于两端柔性直流系统的线路故障行波表达式提取波形特性参数构造保护判据，识别速度快、耐过渡电阻能力好，但复杂网络求解困难，对采样频率要求较高。

以上研究均结合柔性直流线路故障行波的特性，对行波保护判据进行了创新或改进，但仍未能很好地兼顾长线故障下保护速动性和高阻故障识别的问题。文献［19］指出发生区内非金属性故障时，线路端口电流存在独有的短时下降特性，可用于识别区内高阻故障。而实际工程中架空输电线路主要呈感性，电压量比电流量具有更明显的故障特征和更快的响应速度，为改善保护性能提供了更多可能。

在上述研究的基础上，本文通过推导故障电压折反射波的幅值表达式，得出了不同故障位置下到达线路端口的第2 个折射波的幅值特性：区内故障下，该折射波幅值为正，促进端口电压回升；区外故障下，该折射波幅值为负，抑制端口电压回升，且过渡电阻越大，幅值差异越明显。基于此，提出了两段式行波保护方案。以电流变化量和电压变化率作为保护Ⅰ段判据，利用折射波幅值的正负差异和端口电压回升速率的不同构造保护Ⅱ段判据。该方法只需测量单端电气量，判据简单，无需复杂算法，对采样频率要求低；并且延时短，耐受过渡电阻能力强，能快速、准确地识别故障。

1 直流线路故障行波分析简化模型

某一四端柔性直流电网模型如图1 所示，该电网由4 个模块化多电平换流器（MMC）换流站和5 条直流输电线路构成。为提高电网运行的可靠性，换流站采用双极结构［20］，每条线路两端均装设有限流电抗器。图中，Rab为线路a-b直流断路器和继电保护装置；Fab为线路a-b故障；Fa为节点a母线故 障。以R12为 例，F2和F12为 区 内 正 向 故 障，R12应动作以隔离故障；F23、F1和F13分别为区外正向故障和反向故障，R12应避免误动。

图1 四端柔性直流电网拓扑Fig.1 Topology of four-terminal flexible DC grid

1.1 故障行波传播等值网络

发生线路故障时，柔性直流电网正、负极线路之间存在耦合，需通过相模变换公式进行解耦［21］，如式（1）所示。由于0 模分量受线路分布参数影响畸变明显，本文主要分析端口电压1 模分量。

式中：u1、u0和i1、i0分别为端口电压、电流分量在解耦后的1 模分量和0 模分量；uq、un和iq、in分别为解耦前的端口电压、电流正、负极分量。

解耦后，输电线路模域结构与单极系统结构相同。以正极接地故障为例，其相域边界条件如式（2）所示，经过相模变换后，可得到式（3）。由此，可推导出模域故障行波传播的等值网络，见附录A图A1。

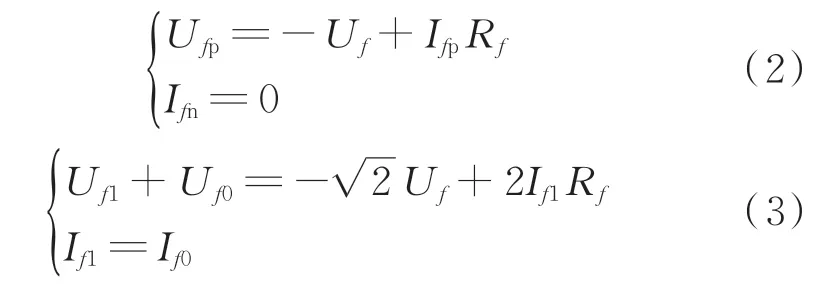
式中：Ufp为故障点f电压的正极分量；Uf为故障前线路额定电压；Ifp和Ifn分别为正、负极故障电流；Rf为过渡电阻；Uf1和Uf0分别为Uf的1 模分量和0 模分量；If1和If0分别为故障时的线路电流的1 模分量和0 模分量。

1.2 故障行波传播折反射系数

基于模域故障行波传播等值网络，利用彼得逊法则可计算出行波在线路边界及故障点处的折反射系数［19，22］，结果如式（4）和式（5）所示。

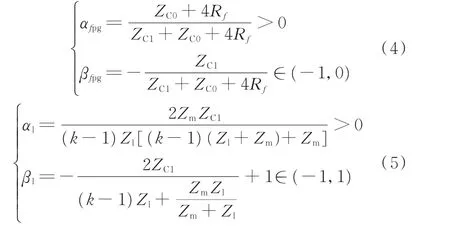
式中：αfpg和βfpg分别为发生单极接地故障时故障点f处的折射系数、反射系数；αl和βl分别为线路边界的折射系数和反射系数；ZC1和ZC0分别为线路波阻抗的1 模分量和0 模分量；Zm为换流站等效阻抗；Zl=(ZC1+sLdc)/(k-1)，其中，Ldc为线路两端限流电抗器电感值，s为拉普拉斯算子；k为换流站出线数。

由于故障电压首行波近似阶跃波，为判断线路边界反射系数βl的正负情况，其在单位阶跃波下的响应见附录A 图A2。可以看出，在不同线路边界条件下，βl的衰减趋势基本一致。因此，一般情况下可近似认为βl＜0。

2 故障行波特性分析

直流输电线路发生区内故障fin和区外故障fout时，故障电压行波的折反射过程如图2 所示，线路12的长度为L12。基于速动性要求，本文仅考虑故障后3τ内行波的折反射过程，其中τ=Lf/v，Lf为故障点f到 端 口1 的 距 离，v为 行 波 波 速。

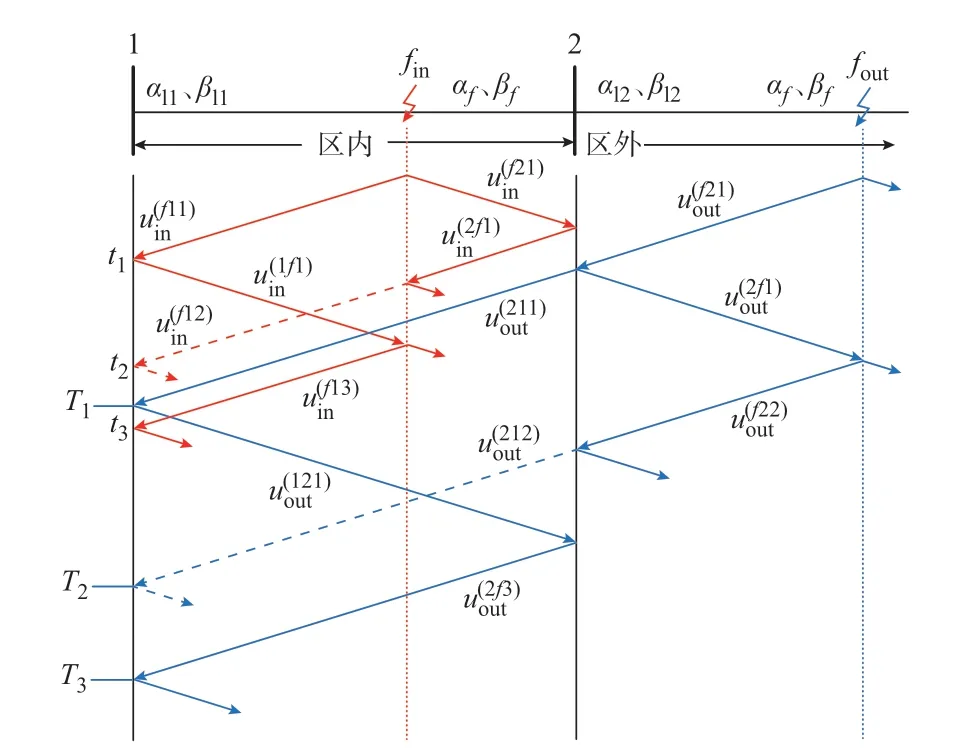
图2 故障电压行波折反射过程Fig.2 Refraction and reflection process of fault voltage traveling wave

2.1 行波时序分析

2.2 线路端口电压理想波形

设故障电压首行波幅值为-U0，结合式（4）、式（5）及图2 可计算出第m个电压波到达端口1 后，端口电压的变化量ΔUm。为简化分析，此处先讨论理想情况，即边界折反射系数均为常数且默认βli＜0，区内、区外故障计算结果如式（6）和式（7）所示。

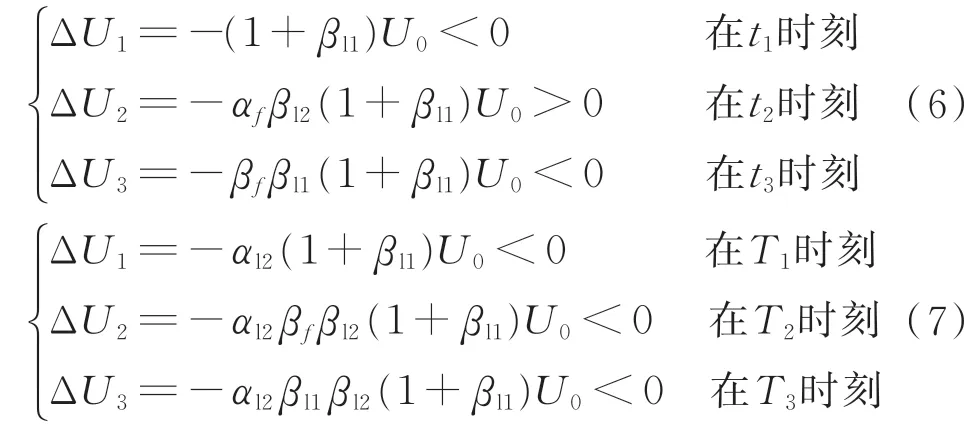
由以上计算结果可得，区内、区外故障下线路端口的第2 个折射波幅值正负相反，可定性画出故障行波的波形图，如图3 中蓝色实线所示。图中，U1、U2、U3表示对应时刻的电压。

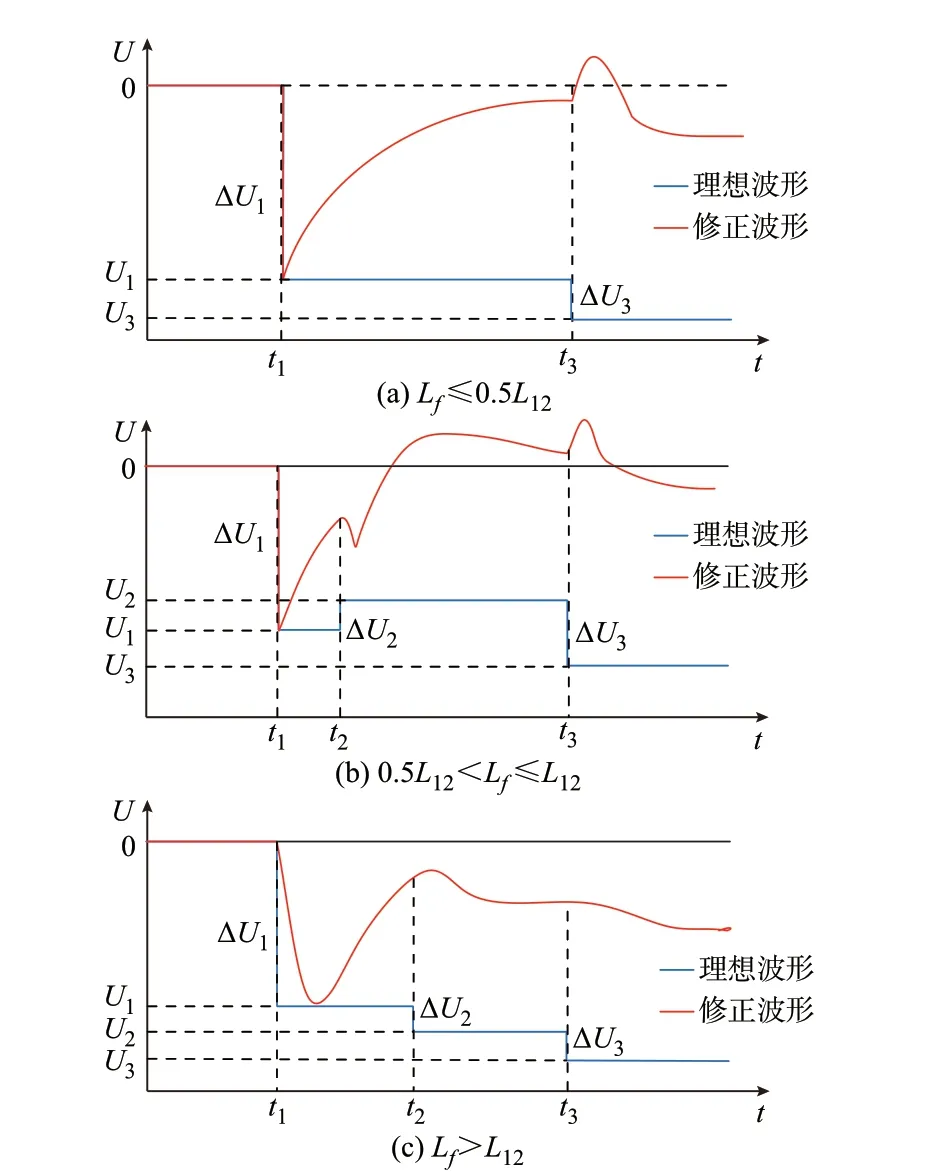
图3 不同故障下保护安装处故障行波Fig.3 Fault traveling waves at protection installation point with different faults

对比可知，Lf≤0.5L12时，由于[t1，t3]时间内无折射波到达端口，端口电压不改变；发生区内后半段故障（0.5L12＜Lf≤L12）和区外故障（Lf ＞L12）时，由于到达线路端口的第2 个折射波幅值正负相反，使得区内故障下端口电压回升，区外故障下端口电压继续下降。由式（4）可知，αfpg随过渡电阻的增大而增大，区内高阻故障下端口电压的回升将更明显。

2.3 线路端口电压实际波形

由于实际工程中架空输电线路一般呈感性，线路电压受时变参数的影响明显。因此，要进一步准确分析波过程，还需考虑βli衰减对端口电压的影响。在式（6）和式（7）中，影响ΔUm幅值的系数项可分为βli、β2li和1+βl1，各系数的取值范围如下。

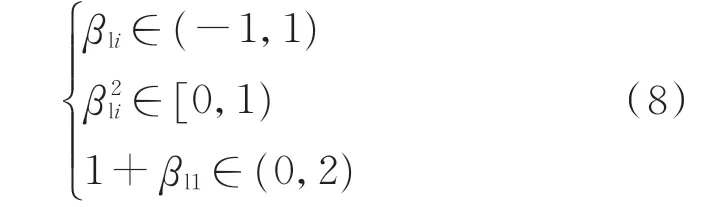
βli的 变 化 趋 势 为1→-1，的 变 化 趋 势 为1→0 →1，1+βl1的变化趋势为2 →0。首先，考虑1+βl1的影响。由1+βl1的变化趋势可知，|ΔUm|将在初始时刻达到最大值，随后急剧减小并趋近于0，不同线路边界条件下ΔU1的变化趋势见附录A 图A3，与上述分析一致。ΔU2和ΔU3在此变化的基础上，其幅值还受βli的影响产生正负跳变。以区内故障下的ΔU2为例，实际波形中ΔU2存在一个由负到正的变化过程。最后，由于平方项非负，且变化相对较小，可近似忽略。

此外，由于线路边界处的限流电抗器具有平波作用，区外故障行波电压变化率一般小于区内故障。修正后的故障行波波形如图3 红色实线所示。

2.4 行波特性总结

发生线路故障后，线路端口电压在故障行波到达的初始时刻降至最低，因边界反射系数βli的衰减逐渐回升。故障位置不同，电压回升过程中的幅值变化也不同。

1）Lf≤0.5L12时，线路端口电压回升仅受βli衰减的影响，最后接近线路初始电压。

2）0.5L12＜Lf≤L12时，由 于 到 达 线 路 端 口 的第2 个折射波幅值为正，促使线路端口电压回升，端口电压回升过程中的最大值将高于线路初始电压。此外，故障距离越长，首行波和第2 个折射波到达线路端口的时间间隔越短；过渡电阻越大，第2 个折射波幅值越大，有利于端口电压的回升。

3）Lf ＞L12时，由于到达线路端口的第2 个折射波幅值为负，抑制线路端口电压回升，端口电压回升过程中的最大值将低于线路初始电压，其回升速率也小于区内故障。

3 基于折射波正负差异的两段式保护

3.1 保护Ⅱ段原理及判据

由第2 章分析可得，故障位置决定第2 个折射波的到达时间及其幅值特性，从而影响端口电压的回升过程。在考虑的时间范围内，无折射波到达时，线路端口所测电压u1的最大值记为ub；有折射波到达时，区内、区外故障下所测得的对应端口电压最大值分别记为uim和uom。根据2.4 节的行波特性分析，ub、uim和uom满足以下关系式：

考虑到限流电抗器的平波作用，区内故障下端口电压的回升速率应大于区外故障，不同故障下端口电压达到最大值的时间不等，使得各故障情况下幅值差异最大的时刻并非在幅值达到最大值的时候。以uom为基准，区内故障的端口电压幅值将先于区外故障的端口电压幅值达到uom（见附录A图A4）。

因此，比较幅值关系时还需考虑时间的影响，可通过缩短保护Ⅱ段的开放时间，提前比较电压幅值，以获得更大的幅值差异。综上所述，基于电压幅值和回升时间构成的保护Ⅱ段判据如下。

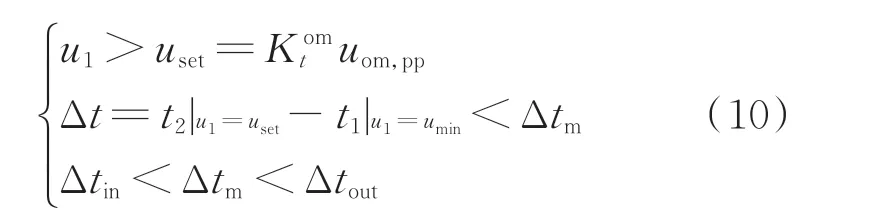
式中：uset为整定值；为时间系数，本文取0.94；uom，pp为发生区外金属性极间故障后端口电压回升过程中测得的电压最大值；Δt为保护Ⅱ段的动作时间；t1和t2为采样时刻；umin为端口电压最小值；Δtin和Δtout分别为保护检测到区内、区外故障下达到动作电压uset所需要的最长、最短时间，前者按线路中点金属性单极故障整定，后者按区外首端金属性极间故障整定；Δtm为保护Ⅱ段的最大开放时间。

3.2 保护Ⅰ段判据

柔性直流电网线路故障电流上升速度极快，可通过测量电流变化量来判断是否有正向故障发生。保护启动后，再通过端口电压变化率识别区内外故障。由于实际计算所得的端口电压变化率为负，保护Ⅰ段判据构成如式（11）所示，各整定值需根据具体电网和各种仿真工况来确定。

3.3 保护流程

综合以上保护判据，可构成完整的保护流程，如图4 所示。端口电压变化率在[εL，εH]之间时，需要开放保护Ⅱ段进一步识别故障位置。然后，通过检测正、负极电压变化量的绝对值之差（ε+和ε-分别为其上、下限）进行故障选极［4］，差值高于ε+为正极故障，低于ε-为负极故障。

图4 保护方案流程图Fig.4 Flow chart of protection scheme

4 参数整定及仿真验证

在PSCAD/EMTDC 仿真平台搭建±400 kV四端五线路柔性直流电网模型，如图1 所示。模型主要参数见附录B 表B1。所有换流站均采用半桥型MMC，线路采用频变参数模型，两端均装有50 mH限流电抗器。本章以线路12 和保护装置R12为例进行仿真验证。

4.1 行波特性验证及判据参数整定

4.1.1 正向故障行波特性验证

分别设置区内前半段高阻故障、区内金属性正极接地故障、区内高阻正极接地故障和区外金属性极间故障进行验证。为提高仿真波形的精度，采样频率设为50 kHz，故障发生时刻为3.0 s，仿真结果如图5 所示。

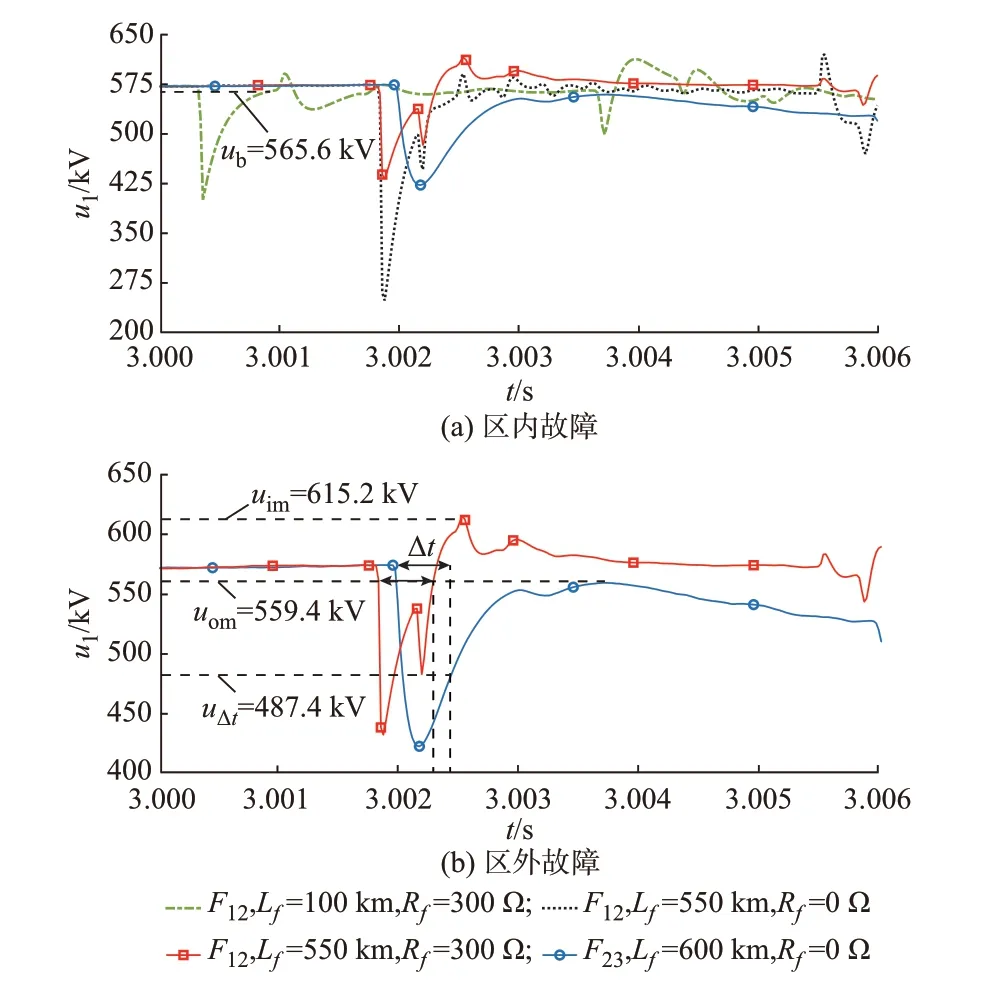
图5 正向故障行波特性Fig.5 Traveling wave characteristics of forward fault

发生区内前半段故障时，回升过程中线路端口电压达到的最大值ub为565.6 kV，接近线路初始电压；发生区内高阻故障时，端口电压的最大值uim为615.2 kV，金属性故障的最大值低于高阻故障；发生区外故障时，端口电压最大值uom为559.4 kV。可以看出，区内、区外故障下电压波幅值特性与1.2 节分析的结果基本一致。

从回升时间的角度对比，在区内故障下，电压上升到uom的时间约为0.5 ms，仅为区外故障的1/3。换言之，区外故障经过与区内故障相同的电压回升时 间 Δt，其 端 口 电 压uΔt并 不 能 达 到 最 大 值559.4 kV，而只能达到487.4 kV。也就是说，只要合理利用电压回升的时间差，缩短保护Ⅱ段的最大开放时间Δtm，就能进一步提高保护Ⅱ段幅值整定值的裕度，以扩大保护范围、提高保护速动性。

4.1.2 反向故障行波特性验证

设置区外反向故障F13与线路正向故障F12、F23进行对比，仿真结果见附录A 图A5。发生反向故障时，线路端口所测得的电流变化量为负值，通过式（11）中的启动判据即可识别区外反向故障。

4.1.3 保护判据参数整定

根据前文所述保护判据整定原则，结合仿真数据可得保护装置R12的整定结果为：δset=0.01 kV，εL=-942 kV/ms，εH=-465 kV/ms，Δtm=0.4 ms，uset=525 kV，ε+=10 kV，ε-=-10 kV。其中，uset按照式（10）所取系数进行整定后，保护Ⅱ段的最大开放时间Δtm在3.1 节所述故障工况下对应的时间范围中选取即可。

4.2 仿真分析

4.2.1 适用性分析

为验证保护方案的准确性和适用性，选取实际工程中常用的采样频率10 kHz，对不同位置、距离、类型的故障进行仿真验证，保护判据识别结果见附录B 表B2，故障前端口电压u1为571.9 kV。

仿真表明，该保护方案能准确识别不同故障类型和故障位置。发生反向故障时，通过检测电流变化量即可防止误动；发生区内极间故障时，由于电压变化率远大于判据整定值，且极间故障的过渡电阻一般较小，也可直接动作，无须开放保护Ⅱ段；发生单极接地故障时，电压变化率可以很好地识别区内低阻故障，但当过渡电阻变大时，区内故障的电压变化率可能小于区外故障而无法判别，此时必须开放保护Ⅱ段进一步区分故障位置。

在保护Ⅱ段开放时间Δtm内，区内、区外故障下端口电压u1的回升速率和幅值有明显差异，与2.4 节 描 述 基 本 符 合。Lf≤300 km 时，u1回 升 的 最大值接近故障前电压；300 km ＜Lf≤600 km 时，金属性故障下第2 个折射波幅值较小，而高阻故障下第2 个折射波的促进作用明显，u1回升的最大值高于故障前电压；区外故障下，u1回升的最大值低于故障前电压，且受第2 个折射波抑制作用的影响，Δtm内电压回升幅值远低于区内高阻故障。此外，由于线路电阻对行波幅值有衰减作用，u1回升的最大值随故障距离增加而有所减小。

4.2.2 影响因素

1）过渡电阻

由附录B 表B2 可知，不同故障距离下的高阻故障均能通过保护Ⅱ段正确识别。因为过渡电阻越大，故障点的折射系数就越大，相应地，区内故障下第2 个折射波的幅值就越大。由于区内外故障下折射波幅值正负相反，与区外金属性故障相比，所造成的端口电压幅值差异就越大。因此，保护Ⅱ段判据有很高的耐受过渡电阻能力。

2）采样频率

由于故障下电压响应速度极快，采样点能否捕捉到电压极值对电压变化率的计算结果有较大影响。低采样频率下，附录B 表B2 中仅有故障距离为300 km 时的高阻故障可由电压变化率判据识别。为进一步分析采样频率对故障识别的影响，分别在10、20、50 kHz 下对区内高阻故障（F12，Lf=550 km，Rf=300 Ω）和区外金属性故障（F23，Lf=600 km）进行仿真验证。仿真结果见附录A 图A6。

可以看出，不同采样频率下，基于采样点差分计算的电压变化率的差异很大，在较低的采样频率下，难以捕捉电压下降极值，导致计算出的电压变化率无法区分区内外故障，保护将失灵。而电压幅值变化对应多点采样，受采样频率的影响较小，区内故障下检测时间的偏差在0.1 ms 左右，区外故障的检测时间几乎不变，低采样频率下保护仍然适用。

3）雷击和噪声干扰

雷击干扰信号属于高频信号，随采样频率的增加，其高频成分对基于暂态量快速变化的电压变化率判据的影响增大［23］。噪声干扰来源于系统或设备内部，附录A 图A7 给出了在信噪比为20 dB 的高斯白噪声干扰下，区内高阻故障（F12，Lf=550 km，Rf=300 Ω）的数据采样结果，采样频率为10 kHz。

从附录A 图A7 中可以看出，噪声干扰造成了电压幅值的波动，但不影响电压的回升趋势。同时，噪声信号与雷击干扰信号相似，能量主要集中在高频部分。由于本文所提方案对采样频率要求较低，有利于减小雷击和噪声干扰对保护的影响。此外，也可利用雷击和噪声信号的频域差异性，在测量环节加入惯性环节或利用分频法进一步减小干扰［4］。

4.2.3 与现有方法的对比

1）传统行波保护方案依赖于电气突变量的峰值，容易受过渡电阻的影响，且低采样频率下难以捕捉到电压变化率峰值。本文方案利用短延时比较电压幅值回升过程中的幅值差异，通过设置保护Ⅱ段补充了传统保护方案的不足。

2）文献［19］所提基于电流的保护方案主要针对线路后半段故障，高阻故障判据检测计算时间为1.6 ms 左右。与之相比，本文方案保护Ⅱ段适用于全线，无需复杂的计算，区内高阻故障下检测时间在0.3 ms 内，区外故障下检测时间不超过0.4 ms，保护范围和速动性均有明显提升。

5 结语

常规行波保护方案在兼顾保护速动性和耐受过渡电阻能力方面有所欠缺，尤其是长线故障下缺乏简单有效的判据。针对此问题，本文通过分析故障电压行波在线路上的传播特性，提出了一套基于电压折射波幅值正负差异的两段式行波保护方案。该方案延时短，耐过渡电阻能力强，可快速、准确地识别故障，而且判据简单、对采样频率要求低、易于实现。主要结论如下：

1）发生区内、区外故障时，到达线路端口的第2 个折射波幅值的正负差异对端口电压有不同的影响：区内故障下，促进端口电压回升；区外故障下，抑制端口电压的回升。

2）基于折射波幅值的正负差异，设置行波保护Ⅱ段。当保护Ⅰ段中的电压变化率判据无法区分区内、区外故障时，短时开放保护Ⅱ段，可确保故障被快速、准确地识别。

本文所提方案需要对电压幅值和保护Ⅱ段开放时间进行配合整定，如何根据实际情况确定最优整定值，有待进一步研究。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。