反例在近世代数教学中的作用

胡江胜，孙丹丹，朱海燕

(1.江苏理工学院 a.数理学院； b.商学院，江苏 常州 213001； 2.浙江工业大学 理学院，杭州 310023)

近世代数又称为抽象代数，作为本科院校数学专业的一门专业必修课，它以研究代数系统的性质与结构为主，是代数几何、代数数论等课程的基础[1-2]。通常，在近世代数教学过程中可以通过两种不同的思路去论证一个命题的成立与否：直接证明其成立性或者举出合适的反例证明该命题不成立。有些命题的直接证明具有一定的难度，但若找出合适的反例则事半功倍。因此，构造合适的反例是近世代数课程教学中的一种重要教学手段和方法，它可以加深学生对抽象代数概念和命题的理解。

1 反例是鉴别假命题的有效方法

近世代数这个严密的系统主要由各种各样的命题组成。命题结论成立的条件和范围是关键所在，但这对学生来说是一大难点，教学过程中经常需要构造相关反例，让学生明确某些概念的重点，澄清其对某些概念不正确的认知，加深对相关知识点的理解。例如，为了让学生更好地理解循环群的性质，可以向学生提出问题：循环群是否在群同态作用下保持[2]。

例1：设群G与群H同态，问G是循环群能否推出H为循环群？反之是否成立。

分析：只需根据循环群的定义验证即可。

(1)先由定义证明，若G为循环群，则H也为循环群。

设φ:G→H为群满同态，群G的生成元为a，取b=φ(a)。容易验证，对任意h∈H，均存在g∈G，使得h=φ(g)=φ(an)=φ(a)n=bn，其中n为整数，所以b=φ(a)为群H的生成元。

(2)再说明若H为循环群，则G不一定是循环群。

例如，令G为有理数域Q上所有n阶可逆矩阵的全体构成的集合，代数运算为矩阵的乘法运算。取H={1}，代数运算为数的乘法运算。作映射φ(A)=1，∀A∈G，则φ是G到H的同态满射，从而G与H同态。但H是循环群，而G不是循环群 (因为G不是交换群)。

又如，为了让学生理解子群之间的关系，可以向学生提出问题：同一个群G上的两个子群的交与并是否仍为群G的子群。

例2：设G1与G2为群G的子群，问G1∩G2与G1∪G2是否为群G的子群？

分析：只需根据子群的定义验证即可。

(1)先由定义证明G1∩G2是G的子群。

设G1,G2是G的两个子群，则G1∩G2≠∅(因为e∈G1∩G2)，显然G1∩G2⊂G。任取a,b∈G1∩G2，因为G1,G2是G的两个子群，所以ab-1∈G1∩G2，于是G1∩G2是G的子群。

(2)再说明G1∪G2不是G的子群。

例如，设G1={2k|k∈Z}，G2={3l|l∈Z}是整数加群Z的两个子群，则G1∪G2={2k，3l|k,l∈Z}。取2,3∈G1∪G2，但2+3=5∉G1∪G2，从而G1∪G2不是Z的子群。

2 反例有利于学生深刻理解抽象的代数概念

近世代数课程中许多概念具有一定的抽象性，脱离具体例子，学生较难真正理解这些概念。如何将抽象的问题具体化，将需要探讨的未知问题转化为学生已掌握的知识是教学重点，通过具体实例讲解，学生更容易理解和接受，且记忆深刻。

例如，为了让学生理解“群”这一抽象概念，只需验证给定集合满足“群”定义中的所有条件即可。

例3：有理数域Q上所有n阶可逆矩阵的全体关于矩阵的加法不构成群。

分析：只需说明可逆矩阵对于矩阵的加法不封闭。

又如，在讲授不变子群的概念时，可以举正反方面的例子，加深学生对该概念的理解。

例4：设N是群G的一个子群，若对∀a∈G，都有aN=Na，则称N是群G的一个不变子群[2]。

正例：N={(1),(132),(123)}是对称群S3的不变子群；反例：N={(1),(12)}不是对称群S3的不变子群，因为N(13)={(13),(123)}≠{(13),(132)}=(13)N。

3 反例有利于学生区别相近的代数概念

近世代数课程中一些概念、性质较类似，初学者容易混淆，如同构映射与同态映射、群的同构与同态、群的阶与元素的阶、置换群与变换群、主理想与最大理想、单位与单位元、左(右)零因子与零因子、理想与子环、零理想与单位理想等容易混淆的概念，可以通过例子(反例)加以说明，使之区别开来[3-4]。

例5：一个集合A的若干个一一变换的乘法作成的群叫做A的一个变换群；一个有限集合A的若干个一一变换作成的群叫做置换群[1]。

从定义的条件上区别：变换群的定义中未必要求是有限集，而置换群一定是在有限集合上定义的；从两者的关系上区别：置换群一定是变换群，而变换群未必是置换群。

反例：令A为整数集合，则A上所有一一变换可构成一个变换群，但却不是置换群 (因为A不是有限集合)。

例6：设R为环，若是在环R中a≠0,b≠0,但ab=0,那么称a是R的一个左零因子，b是R的一个右零因子。若一个元既是左零因子又是右零因子,则称为R中的零因子[1]。

从定义的条件上区别：左零因子a是指用a左乘一个非零元为零元，右零因子b是指用b右乘一个非零元为零元，而零因子要求同时为左零因子和右零因子；从两者的关系上区别：零因子既是左零因子，又是右零因子，而左零因子或者右零因子未必是零因子。

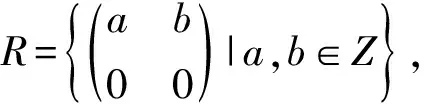
例7：环R中，满足ae=ea=a(∀a∈R)的元e叫做R的单位元。整环R中的一个元ε称R的一个单位，假如ε是一个有逆元的元[2]。

从定义的条件上区别：单位元e可在任意环R上定义，而单位ε一般只在整环R上定义；从个数上区别：一个环如果有单位元则只有一个，而单位可能不止一个；从两者的关系上区别：单位元必是单位，单位未必是单位元。

反例：整数环Z中，单位元为1，单位有±1。

整环Z7={[0],[1],[2],[3],[4],[5],[6]}中，单位元为 [1]，而单位有[1], [2], [3], [4], [5], [6]。

4 结 语

为了透彻理解相关定义、定理及不同概念之间的联系，教师在教学过程中应注重培养学生总结归纳和举一反三的能力，有意识地引导学生重视反例的构造，帮助学生深入理解相关知识点，并在探寻反例的过程中，培养学生思维的逻辑性和严密性。