聚焦含参数的一元二次不等式问题

■赵 军

含有参数的一元二次不等式问题的常见题型主要有四种:求解集问题、求相关系数问题、恒成立问题以及有解问题。掌握常见题型与解题方法,对同学们解答含参数的一元二次不等式问题有一定帮助。

一、正向求解集

例1解关于实数x的不等式:ax2+(a-3)x-3＞0。

解:原不等式化为(ax-3)(x+1)＞0。当a=0时,不等式的解集为{x|x＜-1}。

练习1:解关于实数x的不等式:x2-(a+1)x+a＜0。

提示:由x2-(a+1)x+a=0得(x-a)·(x-1)=0,所以x1=a,x2=1。

故当a＞1时,解集为{x|1＜x＜a};当a=1 时,解集为∅;当a＜1 时,解集为{x|a＜x＜1}。

二、逆向求系数

例2若关于x的不等式ax2+bx-1＞0的解集是{x|1＜x＜2},则不等式bx2+ax-1＜0的解集是( )。

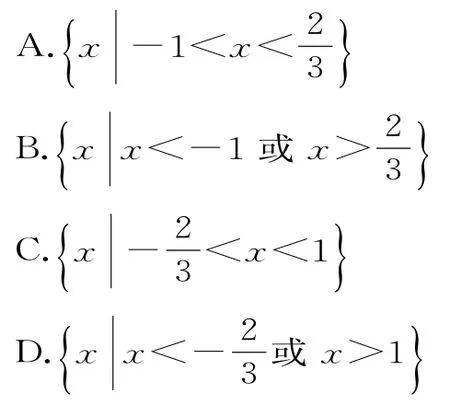
解:由题意可知,1和2是关于x的方程ax2+bx-1=0的两个实根。由根与系数的关系得解得

练习2:已知不等式ax2+bx+2＞0 的解集为{x|-1＜x＜2},则不等式2x2+bx+a＜0的解集为( )。

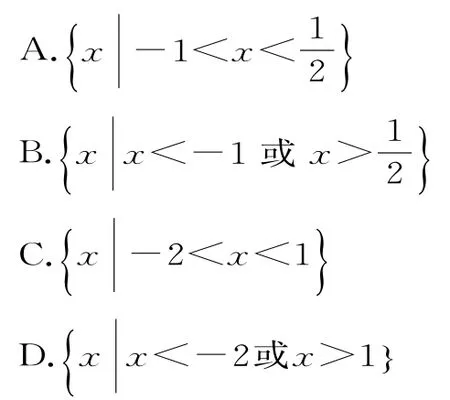
提示:因为不等式ax2+bx+2＞0的解集为{x|-1＜x＜2},所以方程ax2+bx+2=0的两根为-1,2,且a＜0,所以-1+2=,-2=,解得a=-1,b=1。所以不等式2x2+bx+a＜0可化为2x2+x-1＜0,由此解得-1＜x＜。故不等式2x2+bx+a＜0的解集为。应选A。

三、恒成立问题

例3设函数f(x)=mx2-mx-1。

(1)若对于一切实数x,f(x)＜0 恒成立,求实数m的取值范围。

(2)若对于x∈[1,3],f(x)＜-m+5恒成立,求实数m的取值范围。

解:(1)要使mx2-mx-1＜0 恒成立,当m=0时,显然-1＜0 成立;当m≠0 时,由解得-4＜m＜0。故实数m的取值范围是(-4,0]。

(2)由f(x)＜-m+5,可得mx2-mx-1＜-m+5,即m(x2-x+1)-6＜0恒成立。因为x2-x+1=＞0,所以m＜。又因为函数y=在[1,3]上的最小值为,所以只需满足m＜,即实数m的取值范围是。

练习3:已知函数f(x)=x2-+1。∀a∈[1,2],f(x)≥0恒成立,求实数x的取值范围。

提示:由题意可得,∀a∈[1,2],f(x)≥0恒成立。

当x≤0 时,a∈[1,2],显然f(x)=+1≥1＞0恒成立,符合题意。当x＞0 时,由f(x)≥0 恒成立,可得a+恒成立,令函数g(a)=a+,只需满足g(a)max≤x+。当a∈[1,2]时,,所以,解得x∈。

综上可得,x∈。

四、有解问题

例4若关于x的不等式x2-4x-2-a＞0在区间(1,4)内有解,则实数a的取值范围是( )。

A.(-∞,-2) B.(-∞,-2]

C.(-6,+∞) D.(-∞,-6)

解:原不等式等价于存在x∈(1,4),使a＜x2-4x-2成立,即a＜(x2-4x-2)max。

设函数y=x2-4x-2=(x-2)2-6,当x∈(1,4)时,y∈[-6,-2),所以a＜-2。应选A。

练习4:若不等式x2-2x-m＜0在x∈上有解,则实数m的取值范围是( )。

A.[-1,+∞) B.(-1,+∞)

提示:因为不等式x2-2x-m＜0 在上有解,所以不等式m＞x2-2x在x∈上有解。令函数t=x2-2x=(x-1)2-1,则tmin=-1,所以m＞-1。故实数m的取值范围是(-1,+∞)。应选B。