小议恒成立与能成立问题

■宋秀玲

解决不等式恒成立、能成立问题,常见有四种解法:解集法,分离参数法,主参换位法和数形结合法。解答这类问题的方法灵活,能提升同学们的逻辑推理、数学运算等素养。恒成立问题:a＞f(x)恒成立⇔a＞f(x)max,a≤f(x)恒成立⇔a≤f(x)min。能成立问题:a＞f(x)能成立⇔a＞f(x)min,a≤f(x)能成立⇔a≤f(x)max。

题型1:自变量在R 上取值,不等式恒成立,求参数的取值范围

例1设函数f(x)=mx2-mx-1,若对于x∈R,f(x)＜0恒成立,则实数m的取值范围是____。

评注:对于函数f(x)=ax2+bx+c,只有当a≠0时,才是二次函数。当a＞0时,图像的开口向上,当a＜0时,图像的开口向下。

例2已知函数f(x)=asinx-,若对任意的x∈R 都有f(x)≤0,则实数a的取值范围为( )。

A.B.[-1,0)∪(0,1]

C.(0,1] D.(1,3]

评注:解答本题要注意两点:一是正弦函数的有界性,二是换元后新元的取值范围。

题型2:自变量在某个区间上取值,不等式恒成立,求参数的取值范围

例3已知函数f(x)=x2+mx-1,若对任意的x∈[m,m+1],都有f(x)＜0 成立,则实数m的取值范围为____。

图1

对任意的x∈[m,m+1],都有f(x)＜0,只需满足由此代入解析式得解得＜m＜0。故实数m的取值范围是。

评注:画二次函数图像有两个要点:一是看二次项系数的符号,确定二次函数图像的开口方向;二是看对称轴和最值,确定二次函数的具体位置。

例4已知函数f(x)=loga(2x-a)在区间上恒有f(x)＞0,则实数a的取值范围是( )。

“枫桥经验” 以化解基层矛盾纠纷而著称，而调解一直是其基本手段和途径。人民调解制度的创造性运用和发展，是“枫桥经验”长盛不衰、历久弥新的秘诀之一。2011年以来，诸暨市以“枫桥经验”为引领，坚持“大调解、大服务、大发展”的工作思路，努力推进“大调解”体系建设，取得了显著成效。

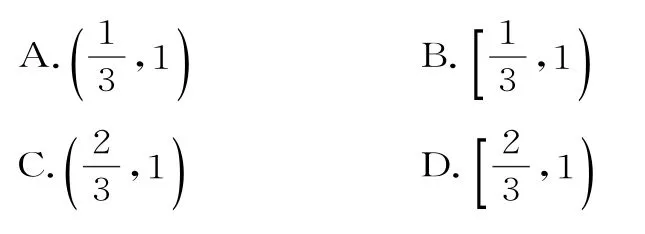
评注:解对数型函数问题,应注意对底数的分类讨论。

题型3:当参数在某个区间上取值时,不等式恒成立,求自变量的取值范围

例5已知函数y=mx2-mx-6+m,若对于1≤m≤3,都有y＜0恒成立,则实数x的取值集合为_____。

评注:转换思维角度,把变量与参数变换位置,构造以参数为变量的函数,再求得原变量的取值范围。

例6已知函数f(x)是定义在R 上的单调增函数,f(1-ax-x2)≤f(2-a)对任意的a∈[-1,1]恒成立,则x的取值范围为____。

令函数g(a)=a(x-1)+x2+1,则解得x≥0 或x≤-1,所以x的取值范围是(-∞,-1]∪[0,+∞)。

评注:在处理多变元问题时,可以选取其中的常数(或参数),将其看作是“主元”,而把其他变元看作常量,从而达到减少变元,简化运算的目的。

题型4:∃x∈R,使不等式成立,求参数的取值范围

例7已知函数f(x)=,若存在x∈R,使得f(x)≥2成立,则实数m的取值范围为____。

令y=2x2-8x+6=2(x-2)2-2≥-2,所以m≥-2,所以实数m的取值范围为[-2,+∞)。

评注:能成立问题可以转化为m＞ymin或m＜ymax的形式,从而求出y的最小值与最大值,即得参数的取值范围。

例8已知命题p:存在实数x,使得不等式x2+2ax+a≤0成立。若命题p是假命题,则实数a的取值范围为_____。

(方法2)若命题p是假命题,则不存在实数x,使得不等式x2+2ax+a≤0成立,即对任意的实数x,不等式x2+2ax+a＞0恒成立,从而Δ=4a2-4a＜0,解得0＜a＜1,即实数a的取值范围是(0,1)。

评注:根据命题真假求参数的方法:利用题目条件,推出每一个命题的真假(有时不一定只有一种情况);再求出每个命题是真命题时参数的取值范围;最后根据每个命题的真假情况,求出参数的取值范围。