均布外压下复合材料球壳脱层跳跃屈曲研究

罗 珊，王纬波

（1.中国船舶科学研究中心 船舶振动噪声重点实验室，江苏 无锡 214082；2.常州工程职业技术学院 检验检测认证学院，江苏 常州 213164）

0 引 言

脱层是复合材料结构常见的损伤之一。制造缺陷或服役期间的低速冲击等都可能使结构产生脱层，在压缩载荷下，脱层的屈曲甚至扩展将引起结构刚度的退化，从而显著降低结构稳定性，导致灾难性后果，对脱层屈曲特性的研究是复合材料结构损伤容限设计方面的重要课题。随着复合材料壳体结构在航空航天、船舶海洋、汽车工业等领域中的广泛应用，其力学性能的研究越来越引起重视，与面内压力下复合材料梁、板结构脱层失稳的机制不同，当复合材料壳体在靠近结构内表面处存在脱层时，在外压作用下，脱层区域会突然从与整体贴合的状态变为分离状态，由上凸构形突变为下凹构形，即发生跳跃屈曲，这种跳跃屈曲是一种有限变形，它的研究不再属于小挠度范畴，需要用到非线性大挠度理论。

结构大挠度屈曲的研究始于杆。欧拉首先研究了一端固定、一段自由的细杆在轴压载荷下的大挠度屈曲问题，他在微分方程的建立时采用了杆弯曲后曲率的精确表达式，所得到的弹性曲线形状称之为弹性线，杆的弹性线方程是一个非线性方程，利用椭圆积分可以得到它的解。由于杆类大挠度屈曲问题的微分方程中均含有二阶非线性项，线性叠加原理将不再适用，方程的求解成为了难点。1962年，Frisch-Fay[1]提出了一种求解薄悬臂梁大挠度弯曲问题的新方法，即弹性相似性原理，他以欧拉杆作为基本模型，通过弹性相似性，将一些悬臂梁弯曲问题转化为等效的基本模型，经过三角函数的代入和坐标变换，可以得到以椭圆积分表示的问题的解。弹性相似性原理绕过了非线性方程的复杂求解过程，引起了很多学者的兴趣，在这个新方法的基础上，他们进行了一系列梁、杆大挠度弯曲问题的研究[2-5]，均得到了满意的结果，从而证实了弹性相似性原理在求解杆类大挠度屈曲问题方面的简便性和准确性。

实验观察到复合材料曲率结构内表面的脱层发生跳跃屈曲时，脱层的屈曲构形与杆的弹性线构形相似，一些学者开始将弹性线模型用于复合材料曲率结构脱层跳跃屈曲特性的研究。Chan 和Mcminn[6-7]将混凝土压力容器内壁的钢制薄层内衬抽象为刚性圆筒内侧的弹性圆环，其在预紧力作用下发生向内的变形屈曲，分别采用正弦函数和弹性线模拟了圆环后屈曲构形，讨论了三种可能的屈曲平衡状态下结构的稳定性以及有限扰动和缺陷对圆环屈曲的影响。Kachanov[8]研究了玻璃纤维管道在外压作用下内层脱落且发生屈曲的问题，利用断裂力学的表面能理论，建立了内层脱落屈曲前后的能量平衡方程，采用弹性线方程描述管道内层屈曲后的构型，得到了临界压缩应力的表达式和最容易发生脱层的内层厚度。Kardomateas[9-10]针对复合材料梁-板结构的长、薄型贯穿脱层建立了“薄层模型（thin film model）”，利用弹性线方程分析了薄层屈曲的大变形效应，讨论了边界条件对薄层屈曲临界载荷的影响，之后他还研究了纯弯曲状态下复合材料梁-板结构的脱层跳跃屈曲问题，以带拐点的弹性线来描述脱层跳跃屈曲后的构型，得到了以椭圆积分表示的临界弯矩的表达式。另外，他还对上述两个问题进行了试验研究，通过对含预埋脱层的复合材料样件的压力试验和四点弯曲试验，得到了与理论结果性质相似的载荷位移曲线，对压力试验值低于理论值的可能原因进行了讨论。Yin[11]对Chen和Mcminn的方法稍作修改，采用浅拱理论、经典弹性线理论、包含横向效应的弹性线方程分别求解了复合材料圆柱壳内表面薄层跳跃屈曲的临界载荷，结果证明基于小变形理论的浅拱理论低估了脱层跳跃屈曲的临界载荷值。Wang和Shenoi[12-14]等基于线性曲梁理论和曲梁大变形理论结合断裂力学分别建立了在开式弯矩和合拢弯矩作用下复合材料曲梁的脱层屈曲模型，阐述了两种情况下脱层屈曲机理的差异，研究了脱层对应角度对极限载荷的影响。

对复合材料结构跳跃屈曲问题的研究，除弹性线模型外，还有其他的理论和模型，一些学者对该问题也开展了试验研究。Hunt等[15]通过四自由度瑞利法分析了受轴压的复合材料杆跳跃屈曲的临界弯矩和后屈曲特性，之后Kinawy 等[16-17]采用简化的三自由度瑞利法研究了同样的问题，并对样件进行了四点弯曲试验，判断了I型和II型两种断裂模式在最终断裂失效起的作用。Bennati等[18]建立了中间含贯穿脱层的复合材料梁四点弯曲试验的一个弹性界面模型，将样件视为由弹性界面连接的三个子层，对脱层子层采用大挠度理论进行分析，得到了脱层发生跳跃屈曲的路径，通过与Kinawy 的试验结果对比，验证了该模型的合理性。Gasco 和Feraboli[19]提出一种用于脱层屈曲扩展非线性有限元分析的自动增量求解算法，在屈曲分析的N-R 法迭代过程中，以裂纹（脱层）扩展长度作为约束变量，求解脱层的前屈曲和后屈曲路径，该法可用于复合材料结构的脱层跳跃屈曲问题，比弧长法更为稳健和有效。Riccio 和Russo[20]等对含脱层复合材料板的受压特性进行了试验研究和数值模拟，试验观察到了试件从整体屈曲到脱层跳跃屈曲的整个过程，采用虚拟裂纹闭合技术对该过程进行了有限元分析，得到了与试验值吻合度很好的结果，证实了脱层的跳跃屈曲与脱层的突然扩展相伴发生。

本文在弹性相似性原理二维模型的基础上对均匀外压下复合材料球壳的脱层屈曲问题进行求解，假设复合材料球壳靠近内表面的部分区域在外压作用下发生脱层跳跃屈曲，采用非线性大挠度理论，以弹性线模拟脱层经线的后屈曲构型，建立脱层区域的弯曲微分方程，基于断裂力学建立屈曲前后的能量平衡方程，利用椭圆积分对方程组进行求解，得到了初始状态含脱层和不含脱层的两种复合材料球壳模型发生内表面脱层跳跃屈曲时的屈曲临界载荷的表达式，对大挠度假设进行了验证，讨论了脱层大小、脱层厚度对脱层屈曲临界载荷的影响，预测了脱层的扩展情况。

1 基于弹性相似性原理的二维模型概述

1.1 圆形薄板弯曲的基本模型

由极坐标表示的圆形薄板小挠度弯曲的基本微分方程为

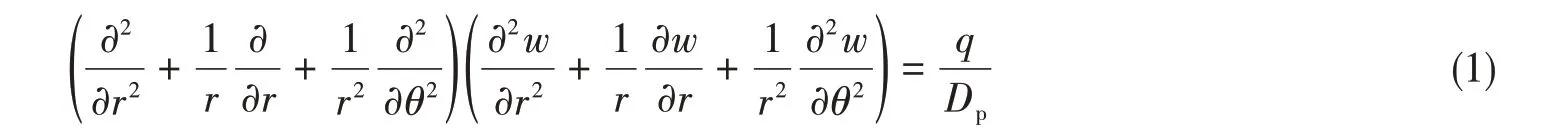
式中，w为圆板横向位移，r为圆板上任一点径向坐标，θ为圆板上任一点周向坐标，q为圆板受到的载荷，Dp为圆板抗弯刚度。

考虑周边简支且受均布弯矩Mp作用的圆形薄板，由圆板理论可以解得

式中，a为圆板半径，νp为圆板材料泊松比。

圆形薄板的任一根径线与纬线弯曲变形后的曲率κr和κθ分别为

再考虑沿周边受均布压力圆形薄板的屈曲，根据板壳稳定性理论，周边简支且受均布压力的圆形薄板的临界载荷（Nr）cr可以通过贝塞尔方程得到，表示为

1.2 基于弹性相似性原理二维基本模型的建立

将同时受压力和弯矩的简支薄圆板作为弹性相似性原理应用的二维基本模型，考虑边界承受均布压力的简支薄部分球壳，可以将其视为是在边界均布弯矩Mp作用下发生了弯曲变形的圆形薄板，如图1（a）所示，因此问题转化为求解边沿上同时受压力和弯矩的简支圆形薄板的弯曲，如图1（b）所示。

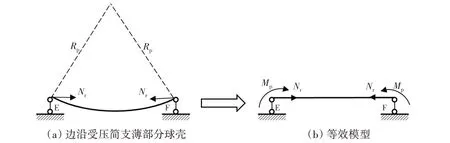
图1 边沿受压简支薄部分球壳等效模型Fig.1 Equivalent model of simply-supported thin partial spherical shell under edge compression

再考虑在边沿EGFH上同时受到压力和弯矩的简支薄部分球壳的屈曲问题，基于弹性相似性原理，将作用在部分球壳边沿EGFH的压力Nr的作用线竖直向上移动一个Mp/Nr的距离，此时在新的边沿E'G'F'H'上，仅作用压力Nr，而不再有弯矩Mp，作用在原球壳边沿EGFH上的弯矩效应已经包含在作用于新部分球壳边沿的压力Nr内，问题化为等效的二维基本模型，即薄圆板在边沿E'G'F'H'同时受压力Nr和弯矩Mp的大挠度弯曲问题，如图2所示。

图2 边沿同时受压弯简支薄部分球壳等效模型Fig.2 Equivalent model of simply-supported thin partial spherical shell under edge compression and bending moment

2 均布外压下复合材料球壳内表面脱层跳跃屈曲研究

2.1 问题描述

假设有一复合材料层合球壳，球壳厚度为T，初始内半径为R0，在靠近其内表面的某深度位置，存在一处平行于壳体中面的脱层，由于脱层的存在，可以将球壳分成3 部分，即不含脱层的子壳S，脱落的薄子壳D 和与子壳D 分离的基底厚子壳B，假设脱落的薄子壳D 的弹性模量为E，泊松比为ν，厚度为t，且t＜＜R0，脱层对球心的张角为2α。

考虑该复合材料球壳在均布外压P作用下脱层屈曲的过程。

状态I：脱层临界屈曲状态，该状态下球壳在P作用下发生整体均匀收缩，内径由R0减小为R，子壳D处于临界屈曲状态，还未与子壳B分离，如图3（a）所示；

状态II：脱层跳跃屈曲状态，假设子壳B 与子壳S 仍保持均匀收缩，未发生屈曲，子壳D 发生了跳跃屈曲，产生了大挠度变形，与子壳B分离，如图3（b）所示。

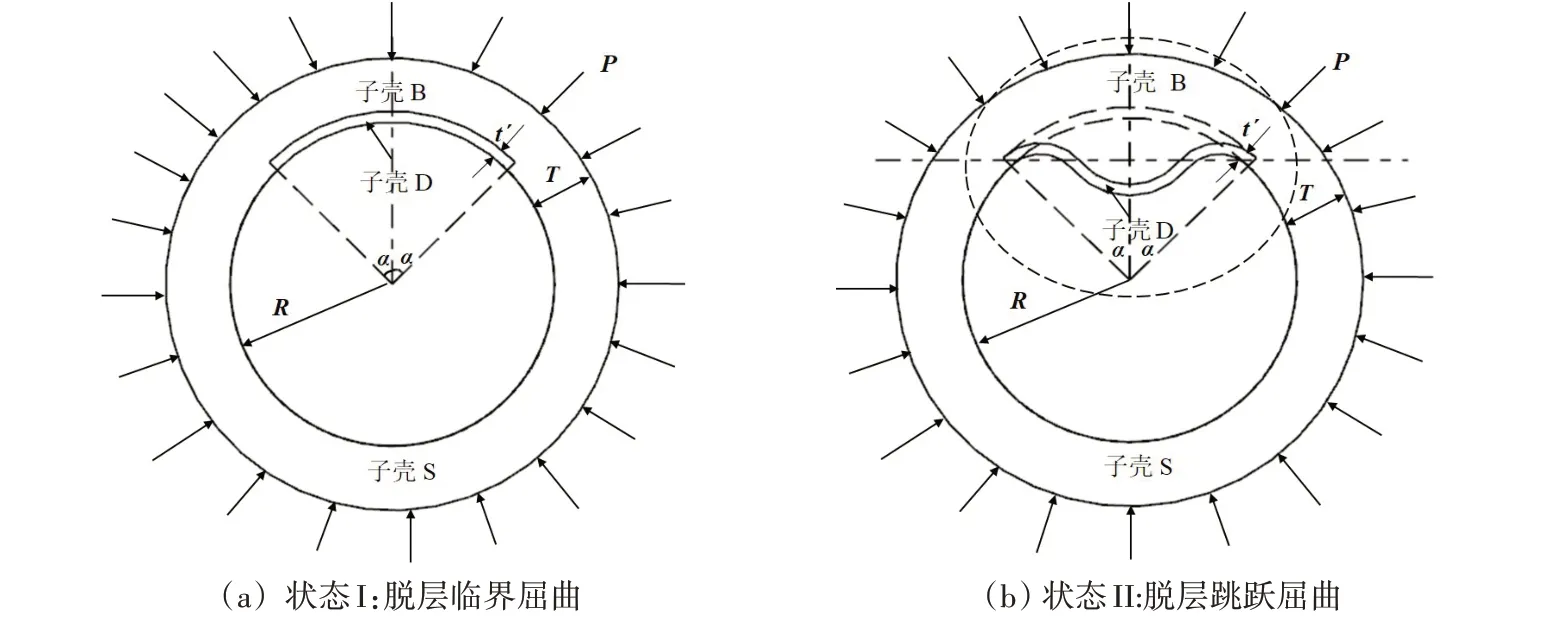
图3 受压复合材料球壳脱层屈曲示意图Fig.3 Schematic of delamination buckling in composite spherical shell under compression

在本文的研究过程中将用到如下假设：

（1）假设脱层子壳D发生跳跃屈曲后的构形相对其中心线是轴对称的，由于子壳D的初始状态是一个球壳结构，其屈曲后完整的研究应该包含经向变形和纬向变形两个部分。本文假设脱层壳体的大挠度变形主要发生在经向方向，纬向变形相对于径向小得多，因此忽略纬向变形效应，这种近似是可以接受的；

（2）假设模型变形在弹性范围内，遵从胡克定律。

2.2 问题的求解

将球壳沿着任意一条经线剖切，得到发生跳跃屈曲区域的局部示意图，如图4 所示。可以看出，子壳D在发生跳跃屈曲后，与子壳B脱离，仅在边沿处受到子壳S的约束且与子壳B相切，屈曲后的平衡状态依靠边沿上的均布压力Pd和弯矩Md来维持，此时子壳D 的受力状态与图2（a）一致，可以利用弹性相似性原理，将其转化为如图2（b）所示的等效模型进行分析。假设子壳D的经线在跳跃屈曲后，其构型为一段含拐点的弹性线，由于该问题为轴对称问题，取对称中心一侧建立局部坐标系，如图5所示。

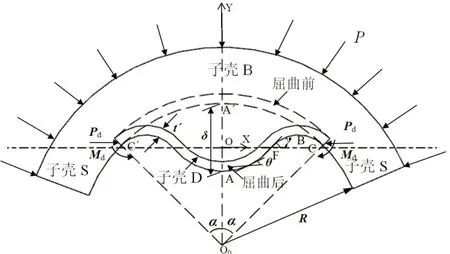
图4 脱层跳跃屈曲局部示意图（沿经线方向剖切）Fig.4 Local schematic of delamination buckling(cutting along the meridian orientation)

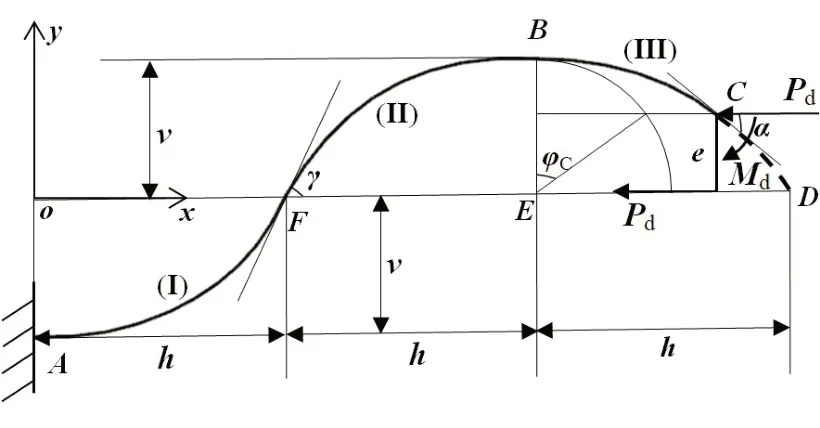
图5 子壳D经线屈曲后构形图Fig.5 Configuration of the meridian of Subshell D after buckling

状态I中临界屈曲时整球均匀压缩，则沿直径方向的径向应变εr和膜应变ε0分别为由于t'＜＜R0，可以认为子壳D在状态I时的半径等于球壳内径R，跳跃屈曲后经线的弯曲平衡方程为

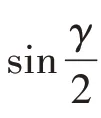
利用椭圆积分可以得到式（7）的解为

式中，F（p,φ）、K（p）代表第一类椭圆积分、完整的第一类椭圆积分；E（p,φ）、E（p）代表第二类椭圆积分、完整的第二类椭圆积分；L表示一段完整的椭圆积分曲线的弧长；v为经线AF、FB段的竖直挠度；e为点C对应的竖直距离；φC为点C对应的φ角。

由于C点对应的角θ为α，将θ=α代入式（9），可得

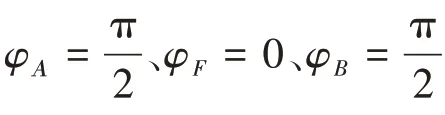
由式（9）和式（10a）可得

在端点C处，屈曲后经线的曲率半径与球壳内径相等，为R，将φC的值代入式（12），整理得

以L0表示初始状态未受外压时的AC长度，L*表示跳跃屈曲后的AC的长度，则有

将式（5）、（6）、（11）、（15a）、（15b）代入式（14），得

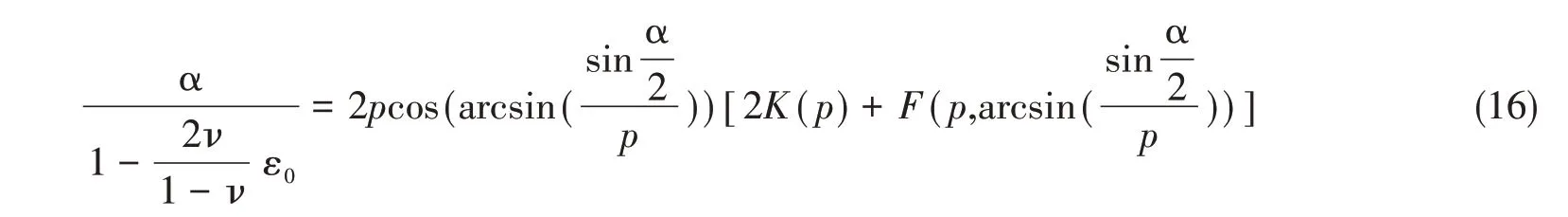
式中，未知数为参数p和临界屈曲时的膜应变ε0。

以上屈曲控制方程的建立是基于屈曲后构形的大挠度假设，对于这样一种构形发生的必要条件是：脱层在状态I的应变能必须大于或等于状态II的应变能。将靠近内表面区域的局部脱层视为壳体结构的内部裂纹，结合断裂力学的能量理论，得到子壳D屈曲前后的能量平衡式为

式中，U0为屈曲前子壳D的应变能，UB为跳跃屈曲后，子壳D的应变能，W为发生脱层的断裂能。

状态I时，球壳受压均匀收缩，处于临界屈曲状态，此时子壳D的应变能U0可表示为

状态II时，子壳D的应变能主要是由屈曲后三个区域的弯曲应变能组成，即

式中，UI、UII、UIII分别代表I、II、III区的弯曲应变能。

对I、II、III三个区域的弯曲应变能分别考虑，则

式中，χi为i区域屈曲前后的曲率变化，dAi为i区域的面积微元。

对于I区域，在跳跃屈曲后，该区域的经线发生了翻转，曲率由凸变凹，故

对于II、III区，经线曲率变化为

将椭圆积分的解以及刚度D、φA、φF、φB的值代入式（20），化简整理得

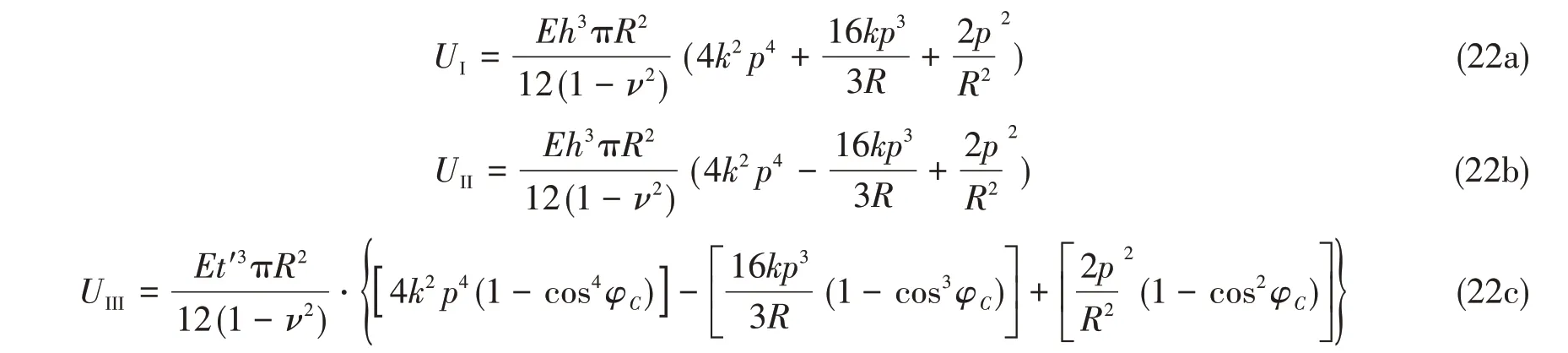
将式（22）代入式（20），整理得

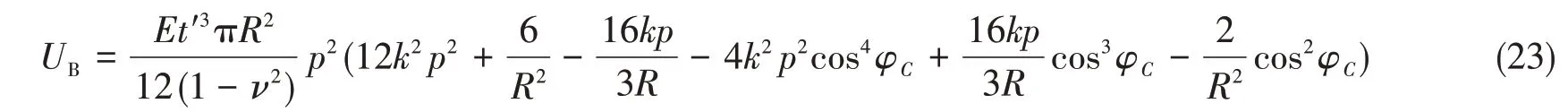
由断裂力学理论，断裂能W可表示为

式中，Γ为材料参数，指的是产生新裂纹所需要克服的表面能。

由式（9）得

代入式（13），整理可得

将式（11）、（18）、（23）、（24）、（26）代入式（17），整理后可记作

就医前应想好病情描述，最好能说清整个前后病程的时间、症状、化验及检查结果、用药及用药的效果，病情复杂的可以列个表写下来，有些不方便直接带给医生看的可以拍下来给医生看。药要能说出药名，最好是药品名而不是商品名，记不住的可以把药盒子带上，病情叙述简明扼要一点。

式中，

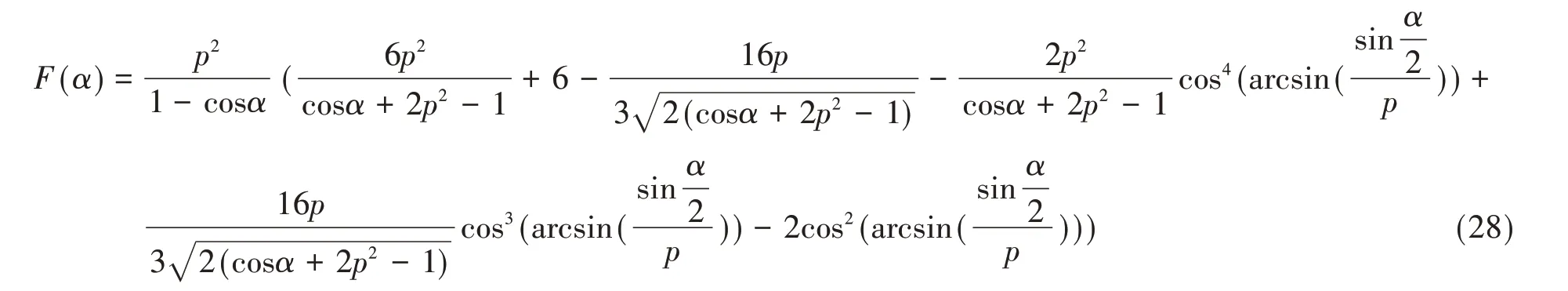
在方程（27）中，未知数为参数p和临界屈曲时的膜应变ε0，结合方程（16），2 个方程对应2 个未知数，故问题可解。

3 结果与讨论

3.1 大挠度假设的验证

考虑脱层发生跳跃屈曲后的挠度，从图4可以看出，屈曲后经线的最大位移位于子壳D的中心，该点由A'移动到A，设该距离为δ，则

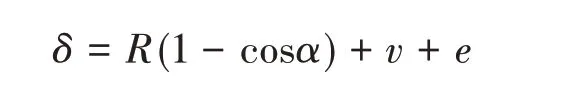
将式（10c）、（10d）、（26）代入上式，整理得

文献[6]指出，复合材料曲率结构发生脱层屈曲时，根据脱层区域的大小，对应不同的屈曲路径，存在一角度α*，当脱层对应张角2α＜2α*时，脱层区域发生小挠度屈曲；当脱层对应张角2α＞2α*时，脱层将发生大挠度跳跃屈曲。该α*的大小与R/t'的大小有关，α*随R/t'的减小而增大。本文讨论R/t'值为800、400、200、100 四种情况下，脱层发生跳跃屈曲时的特性，估算当α＞15°时，上述四种情况均可发生脱层的跳跃屈曲，得到R/t'值为800、400、200、100 四种情况下，最大位移与脱层大小和厚度的关系，如图6所示。

图6 最大位移与脱层参数关系Fig.6 Relationship between maximum displacement and delamination parameters

从图6 可以看出，脱层屈曲后的最大位移与脱层的大小和厚度有关。当脱层厚度一定时，初始脱层越大，则屈曲后脱层的最大位移越大；当脱层大小一定时，脱层的厚度越大，屈曲后脱层的最大位移越小。当初始脱层的大小在15°～90°时，最大位移与脱层厚度的比值范围为5～1200，符合大挠度的假设。

3.2 受压复合材料球壳脱层跳跃屈曲的特性分析

将式（5b）代入式（27），整理可得复合材料球壳内表面薄层发生跳跃屈曲的临界载荷Pcr为

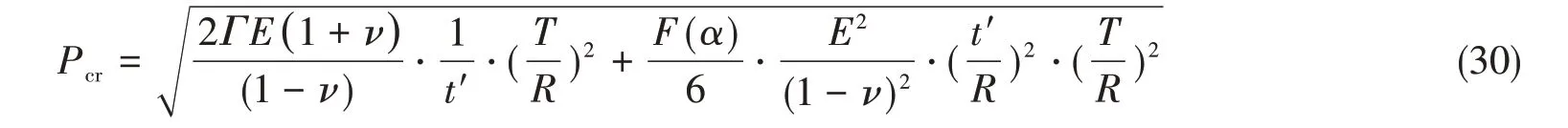
3.2.1 初始状态下含脱层复合材料球壳的脱层屈曲特性分析

假设复合材料球壳初始状态下在靠近其内表面存在脱层，此时可以令式（30）中Γ值取0，可得脱层发生跳跃屈曲的临界载荷为

图7 临界屈曲载荷与脱层参数关系Fig.7 Relationship between critical buckling load and delamination parameters

图8 F(α)与脱层参数的关系Fig.8 Relationship between F(α)and delamination parameters

式中，

由于G值近似为一常数，说明对于初始状态下含内表面薄层脱层损伤的复合材料球壳，其脱层的临界屈曲载荷与脱层与球壳的厚度比（t'/R）近似成正比，在球壳厚度一定的情况下，脱层位置越靠近球壳内表面，薄层发生跳跃屈曲的临界载荷就越小。

3.2.2 初始状态下不含脱层复合材料球壳的脱层屈曲特性分析

假设复合材料球壳初始状态无脱层存在，将F0代入式（30），可得厚度为t'的薄层脱离整体并发生跳跃屈曲的临界载荷Pcr2为

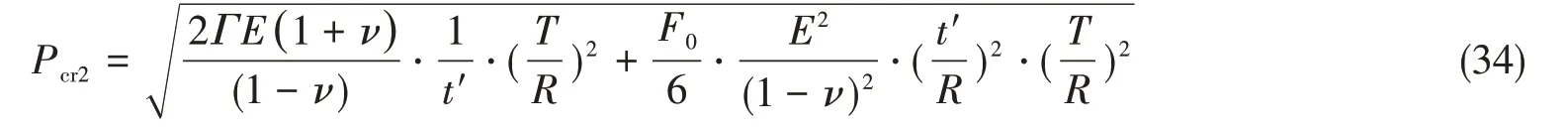
仍取F0=30，上式整理得

从图9 中可以看出，与上小节中初始状态含脱层球壳的脱层临界屈曲载荷随着脱层厚度的增大而增大不同，初始不含脱层的层合球壳受压产生内表面薄层脱层屈曲的临界载荷主要依赖于脱层的厚度t'，当脱层厚度很薄时，随着脱层厚度的增加，脱层屈曲的临界载荷也随之下降，直到达到某一最小值Pcr2min之后，临界屈曲载荷将随脱层厚度的增加而增大。

图9与脱层厚度关系Fig.9 Relationship between and delamination thickness

设

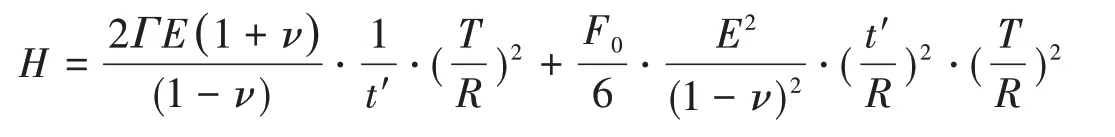
由式（34）可得，当H值最小时，Pcr2值最小。

当且仅当

时，Pcr2有最小值Pcr2min，

此时Pcr2min对应的薄膜脱层厚度t'cr为

t'cr表示在层合球壳结构中，在靠近其内表面区域，存在最有可能发生脱层并屈曲的某一位置，其对应着脱层临界载荷Pcr2min，如果层合球壳结构在设计时，并不能确定是否存在脱层或者脱层的具体位置，则应将Pcr2min作为结构产生脱层并发生脱层屈曲的最小临界载荷值。

对比式（31）和式（34），Pcr2的表达式相对于Pcr1多了包含Γ的一项，表示当球壳初始状态不含脱层时，从产生脱层到脱层发生跳跃屈曲，除了维持大挠度构型平衡状态的能量之外，还需要能量来克服脱层与整体发生分离前的层间强度。如果界面层间强度不足，即表面能Γ值非常小时，则产生脱层和脱层屈曲的临界载荷主要取决于含F（α）的一项，从物理含义上看，函数F（α）随α角的变化趋势体现了一定载荷范围内脱层的扩展情况。上述分析中已经证明，在表示脱层大小的α角对应的（15°，60°）区间内，F（α）增长非常缓慢，因此其对应的脱层屈曲载荷值的增加也非常小，意味着一旦靠近球壳的内表面区域产生脱层，无论是初始状态就存在的脱层还是受压后产生的脱层，即使开始是一个较小的脱层，在外压达到其临界屈曲载荷值后，脱层将首先发生屈曲，且在该载荷下脱层区域很可能发生进一步扩展，从而引起内表面薄层沿着层合界面发生大范围脱落，最终导致结构的崩溃。

4 结 论

本文所描述的是一种大挠度非线性屈曲模型，从以上的分析可以得出受压复合材料球壳内表面薄层跳跃屈曲的一些特性：

（1）如果复合材料球壳在靠近内表面的区域，初始状态即存在脱层，则随着外压的增加，球壳先是均匀收缩，当外压达到脱层的屈曲临界载荷时，内表面的薄层将发生屈曲。脱层屈曲的临界载荷值与初始脱层的大小和厚度有关，初始脱层越大，脱层屈曲的临界载荷值越大；脱层的区域越厚，脱层屈曲的临界载荷值越大，脱层的临界屈曲载荷值与脱层和球壳的厚度比t'/T几乎成正比。

（2）若复合材料球壳初始状态无脱层存在，则在受均匀外压时，如果层间强度不足或受到其他扰动因素，其靠近内表面的薄层有可能从球壳整体脱落且发生跳跃屈曲，存在最有可能发生脱层屈曲的某一位置，其对应的脱层临界屈曲载荷最小，该值可以作为设计层合球壳结构时的稳定性下限值。

（3）根据本文分析，无论复合材料球壳结构中是否存在初始脱层，一旦产生脱层并发生跳跃屈曲，如果沿着脱层与球壳结合界面的强度不足，在发生屈曲之后，脱层很容易发生进一步扩展，即内表面薄层沿着层合界面发生大范围脱落，从而导致结构的崩溃。