水下连接器金属密封圈裂纹故障对密封性能的影响

安维峥,王莹莹,刘国恒,汪 聪,段梦兰,刘云迪

（1.中国石油大学（北京）安全与海洋工程学院,北京 102249;2.中海油研究总院有限责任公司工程研究设计院,北京 100028）

0 引 言

水下管道连接器是水下生产系统必不可少的关键装备，主要用于水下装备连接时的密封，使其形成油流的密封通道，防止海洋油气泄漏，保障海上油气田高效开发的安全可靠性。水下连接器长期工作于海底，不仅受到海底的波浪海流等环境因素的影响，而且在外部环境载荷和内部流体的压力以及腐蚀等因素的联合作用下，可能诱发其产生密封部件裂纹、腐蚀或者断裂，导致轻微的原油泄漏，严重者可能导致一口或多口井关井停产，造成大量的经济损失。一旦发生严重的原油泄漏，其危害难以估计，作业公司不仅承受关井和原油流失的损失，后续的清理浮油工作更要耗费巨额资金，甚至导致人员伤亡、海洋环境严重污染、海洋生态系统被破坏等[1]。因此，探究水下连接器密封圈的密封性能，及时找到其裂纹的成因及发展规律，预防油气泄露，是水下生产系统生产维护中的关键问题。

针对水下连接器故障与密封性能方面的研究，国内外学者已做了大量工作。2005年，Fassina 等[2]对12个卡爪结构的水下连接器进行了有限元模拟和实验研究，分析出卡爪断裂的原因;同年，胡勇等[3]对救生钟在水下对接过程中和对接后的密封性能做了全面分析，研究了在各种密封失效形式下，不同海流、对接深度、对接角度等多种影响参数综合作用下的救生钟密封性能；2015 年，万波等[4]研究了连接器的失效原因、失效形式，并利用故障树法定性分析了驱动环的可靠性；2016 年，曹伟枫[5]建立了水下井口连接器的简化力学模型和有限元分析模型，研究了连接器密封圈的密封接触特性和疲劳寿命，推导出驱动环上的驱动力与连接器受到的内压以及预紧力的关系式；2017 年，Zhang 等[6]提出了连接器密封机构抗压能力的理论计算方法，通过分析不同部件之间的载荷传递关系推导出了密封接触载荷与锁紧力之间的关系表达式，并利用建立的透镜密封圈与法兰的接触模型推导了压缩解析表达式;2019 年，蔡志杰等[7]在ABAQUS 平台应用新的动态接触法，分析了水下连接器试压帽在安装和试压过程中的密封接触特性，研究了其与等效锁紧力矩的关联性；同年，程子云等[8]介绍了一种锁块式连接器的结构和原理，利用有限元方法分析了安装、锁紧、钻完井和生产四种工况下的密封连接性能，得到了井口采油树接触力、密封圈接触应力以及锁紧块受力情况与外载的关系表达式;同时，曾威等[9]利用有限元方法并应用Norsok腐蚀模型，把密封接触强度当作密封性能的评价指标，得到了密封接触强度随时间的变化曲线。

综上，从国内外研究现状可知，目前对于水下连接器密封性能的研究多停留在影响参数和接触特性等方面的研究，缺乏针对预置裂纹的水下连接器裂纹故障的密封性能研究。因此，本文针对水下连接器金属密封圈的预置裂纹故障，探寻不同裂纹损伤参数对密封圈密封性能与结构性能的影响，对于提高水下连接器在实际工程应用中的安全可靠性具有重要的参考价值。

1 金属密封圈密封失效准则与判断标准

1.1 金属密封机理

水下连接器的主要结构如图1 所示，包含连接盖、驱动环、卡爪、对中底座、上毂座、金属密封圈、下毂座。锁紧过程为：液压力推动驱动环向下运动，同时带动与其紧密贴合的卡爪收拢，卡爪将上、下毂座卡紧，挤压处于中间的密封圈，产生密封接触区域。液压力通过接触面的传递，最终转化成毂座与密封圈之间的压缩载荷，使密封圈产生变形，填充毂座表面和密封圈表面的微观间隙，形成有效密封[10]。

图1 水下连接器结构示意图Fig.1 Structure of subsea connector

1.2 金属密封准则

由GB150—2010 可得到金属密封的判据，因为水下连接器密封圈属于钢制金属环，故取垫片系数m为6.5，密封比压y为179.3 MPa。标准中密封件满足密封性能的要求为：预紧工况时，接触面应力需大于密封比压；工作工况时，接触面应力需大于垫片系数和工作内压的乘积。同时，文献[11]指出，总密封宽度至少在1.5～2 mm 以上时，才能实现金属密封圈可靠密封。因此本文建立如下密封设计准则：

（1）q0＞y，b≥2 mm；

（2）q＞mp，b≥2 mm。

式中，q0为预紧接触应力，q为工作接触应力，y为密封比压，m为垫片系数，p为工作内压，b为有效密封宽度。

2 水下连接器金属密封力学模型分析

2.1 预紧工况

预紧工况下，对锥形密封面进行受力分析，结果见图2。图中，Fn0为垂直于密封面的挤压力；Ff0为密封件受到的摩擦力；G0为Fn0与Ff0的合力；W0为G0在垂直方向的分力，即轴向预紧力；NR为G0在水平方向的分力，即密封面的回弹力。预紧时，在锥面上的法向挤压力大小为

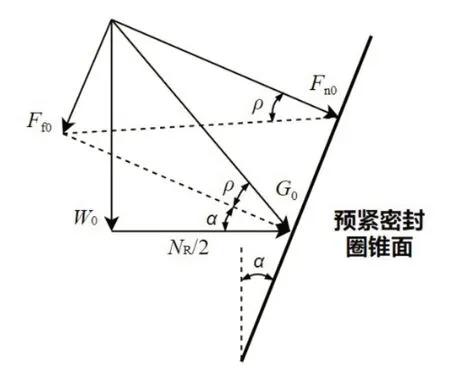
图2 预紧时的密封面受力分析[12]Fig.2 Force analysis of preload sealing surface

式中，Dm表示密封圈中径，单位为mm；b是接触面有效宽度，单位为mm；q0表示预紧时的接触应力，单位为MPa。

由于连接器卡爪的收紧，相对于上毂座，密封圈有向上移动的趋势，所以密封面上的摩擦力Ff0方向向下，Ff0与Fn0的合力G0为

式中，ρ表示两个接触密封面之间的摩擦角，钢和钢接触时取ρ=8.5°[13]。

G0在垂直方向的分力为轴向预紧力W0，在水平方向的分力为密封圈被压缩后材料自身产生的回弹力NR，单个密封面上的力为NR/2，即

式中，α为密封圈锥面与竖直方向夹角。

预紧结束后，密封圈的压缩量达到最大状态。设径向压缩量为2Δ时，则密封圈上的周向应变εθ及周向应力σθ为

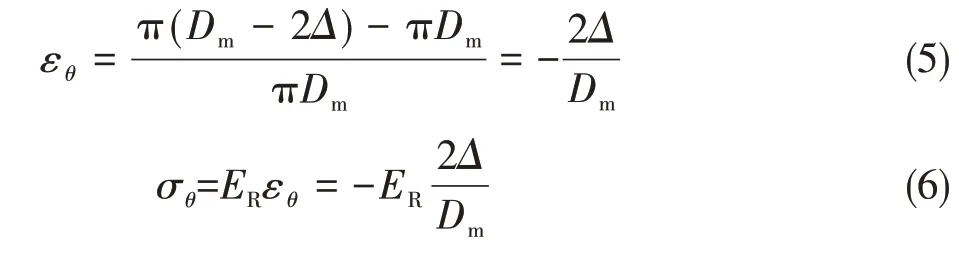
式中，ER为密封圈材料的弹性模量，单位为MPa。

由于是轴对称结构，取二分之一密封圈进行受力分析，受力图如图3所示。根据静力平衡可得

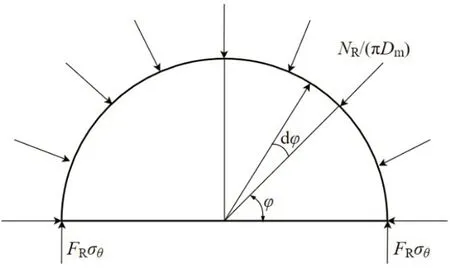
图3 密封圈的环向静力平衡Fig.3 Circumferential static force equilibrium of the sealing ring

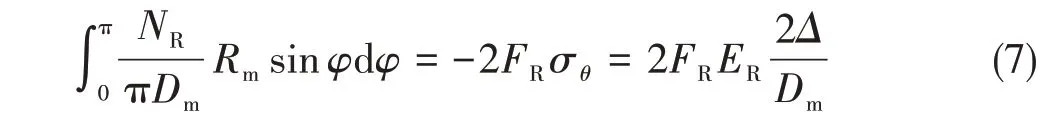
式中，NR/πDm为密封圈周向单位长度上的回弹力；FR表示密封圈截面积，单位为mm2；Rm表示二分之一中径，单位为mm。

由式（7）可得回弹力NR和周向应力σθ的关系为

结合式(3)及式(4)，可得接触面压力q0与径向压缩量Δ的关系为

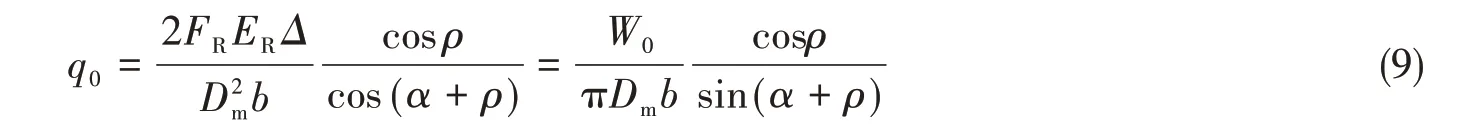
可知，预紧时密封面接触应力主要取决于密封圈的径向预压缩量Δ或轴向预紧力W0。

2.2 工作工况

工作时，密封圈受到的轴向力由四个部分组成：预紧时的轴向预紧力W0、内压垂直作用在连接器上产生的轴向载荷Wp、内压径向作用在密封圈内表面而产生的轴向载荷W1和密封圈发生回弹后的回弹力产生的轴向载荷W2。对连接器做静力学分析，得到连接器在预紧力反方向上受到的合力为

式中：Δ'为密封圈回弹后径向压缩量，单位为mm；h表示密封件在垂直方向的高度，单位为mm；p为工作内压，单位为MPa；Sp表示连接器上轴向受到的内压面积，单位为mm2。

在内压逐渐增大的过程中，一开始压力产生的轴向力小于毂座的自重，此时毂座没有上抬，密封圈保持预紧时的径向压缩量，密封锥面上的压紧力由三个力的合力提供，分别为预压缩量回弹产生的回弹力NR/2、内部液体压力作用的径向载荷Np/2 及轴向预紧力W01，此时密封锥面上的预紧力最小。其中，轴向预紧力W01为内压垂直作用在连接器上的轴向载荷、毂座自重和预紧力的合力。

内压继续增大，毂座被向上抬起，密封锥面上的接触压紧力只有W″，

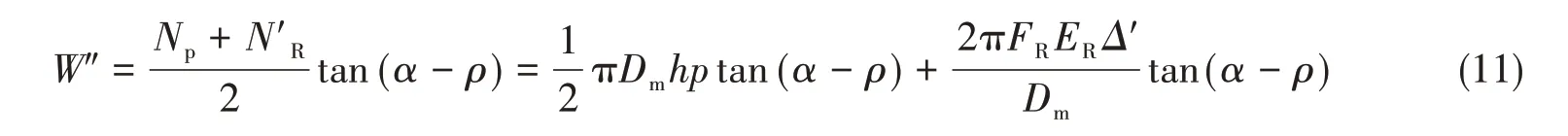
密封面压力q为

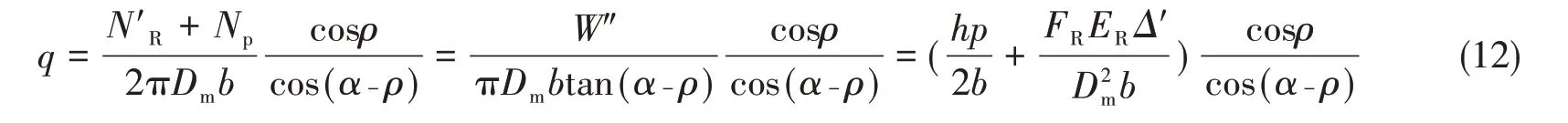
但是，以上接触应力计算公式具有一定的局限性：一是根据理论需要知道密封圈具体结构与材料的参数，计算比较复杂；二是得到的接触应力是理想状态下的集中力，对于要求形成连续密封的金属密封圈来说，所得到的接触应力参考价值不大；三是该公式没有考虑裂纹因素的影响，无法准确计算含裂纹故障密封圈的接触应力。下面给出了一种有限元的数值计算方法，可采用ABAQUS 软件的接触求解功能，直接求得含裂纹故障密封圈的接触应力分布，以满足研究需求，并且将理论公式计算值与有限元分析计算值作了对比，说明有限元计算方法的必要性。

3 无裂纹金属密封圈模拟分析

3.1 有限元模型建立

水下连接器三维模型如图4（a）所示，为了简化计算，将水下连接器核心的密封圈与上下毂座组成的密封组件作为研究对象，简化模型如图4（b）所示。

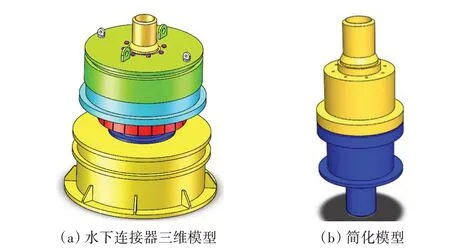
图4 水下连接器模型Fig.4 Models of subsea connector

对模型进行全局网格划分，为了更准确地得到密封圈接触面的应力与接触状态，利用边界种子对密封圈接触面进行详细网格划分[14]。将密封圈与毂座的接触面网格分为10份，每份网格为0.5 mm。

水下连接器工作状态下与管道内部的高压油气流体、外部的海水直接接触，因此连接器直接受到的载荷有内部油气的内压、外部海水外压和轴向预紧力。根据实际情况，设内部油气压力为34.5 MPa，垂直作用在上毂座、下毂座和密封圈的内表面上；外部海水压力为15 MPa，作用在下毂座外表面；施加到上毂座端面的预紧力为445 kN；预紧与工作工况下，约束下毂座端面竖直方向的运动。整体网格划分结果、接触面11个网格节点分布情况与载荷施加情况如图5所示。

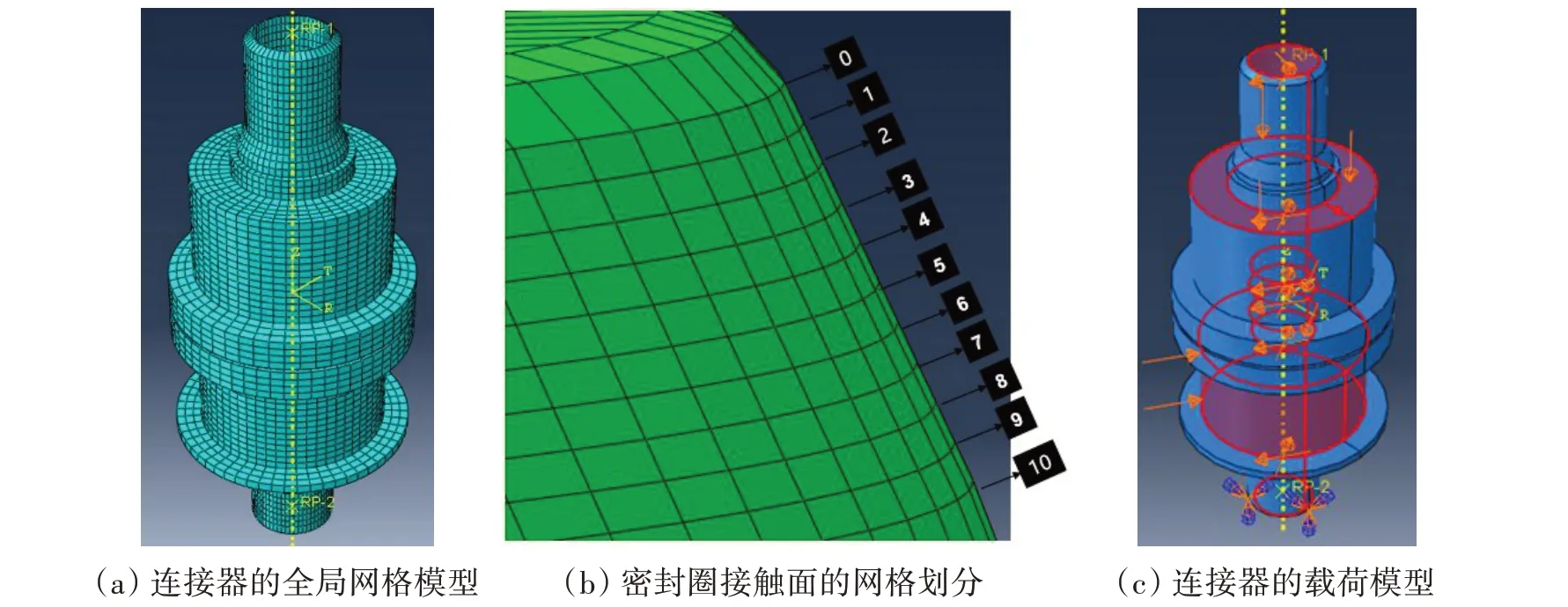
图5 网格模型与载荷模型Fig.5 Meshing and loading models

3.2 材料属性

由于金属密封圈的工作环境，应该选择屈服强度高、塑性良好且耐腐蚀性能较好的金属材料以满足工作要求。各部件的材料参数见表1，其中Inconel 625的应力应变曲线如图6所示[15]。

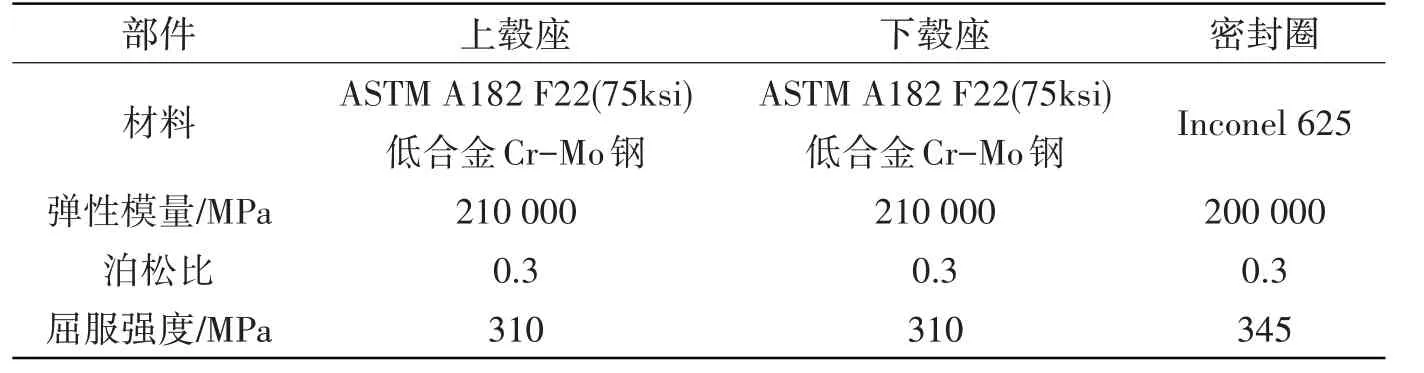
表1 各部件材料参数Tab.1 Material parameters of different parts

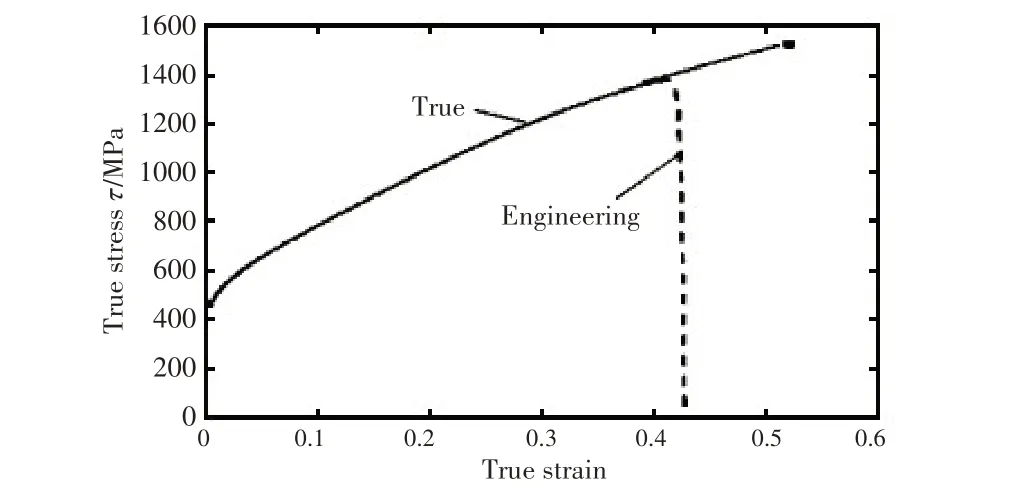
图6 Inconel 625应力应变曲线Fig.6 Relationship between plastic deformation and stress of Inconel 625

3.3 接触分析参数设置

接触问题为状态非线性问题，接触面间的相互作用包括法向作用与切向作用。对于法向作用，ABAQUS中接触压力与间隙的默认关系是“硬接触”，即只有当两表面之间完全无间隙时才施加约束。对于切向作用，ABAQUS中常用的摩擦模型为库仑摩擦、罚函数模型等，罚函数模型允许接触面有“弹性滑移”。本文选择罚函数的摩擦模型，定义摩擦因数为0.15[16]。本文的金属密封圈模型有2对接触，即上、下毂座分别与密封圈的接触。

3.4 无裂纹密封圈的有限元分析结果

无裂纹密封圈两种工况下的等效应力和等效塑性应变的分布如图7所示。预紧工况的最大等效应力值为454.2 MPa，最大等效塑性应变值为0.001 2，工作工况的最大等效应力值为467.1 MPa，最大等效塑性应变值为0.003 8，位置都出现在密封圈与毂座的接触面处。两种工况的最大等效应力值均大于密封圈屈服强度345 MPa，可知由于预紧力、介质压力等的作用，密封圈与毂座的接触面发生了一定程度的塑性变形，为后节预置裂纹分析提供了参考区域。

图7 无裂纹密封圈的有限元分析云图Fig.7 Finite element analysis of sealing ring without crack

4 预置裂纹的水下连接器金属密封圈模拟分析

4.1 预置裂纹

无裂纹密封圈最大等效应力位置与最大塑性变形位置都在密封圈与毂座的接触面上，该区域是决定密封性能的重点研究区域。为了研究裂纹的深度、位置、角度对水下连接器密封性能的影响，在密封圈与毂座的接触面上，分别设置了不同深度、位置、角度的裂纹。其具体参数定义如图8所示。

图8 预置裂纹参数Fig.8 Parameters of the preset crack

4.2 不同裂纹参数对密封性能的影响

（1）裂纹深度对密封性能的影响

采取的裂纹深度为0.5 mm、1 mm、2 mm、3 mm、4 mm和5 mm。取节点3的接触应力为参考值，得到不同裂纹深度时的节点3 处接触应力与有效密封宽度的变化趋势如图9 所示。对比1.2 节密封标准，预紧工况与工作工况的有效密封宽度均符合不小于2 mm 的要求。且裂纹深度越深，节点3处接触应力基本趋于增大，密封宽度也越大。

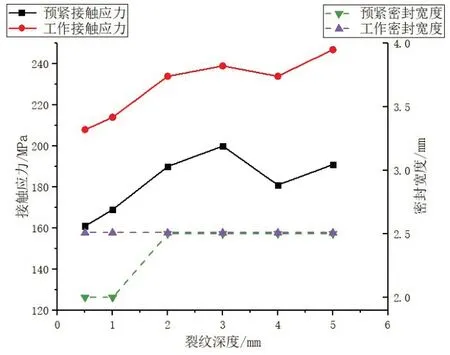
图9 节点3接触应力、密封宽度与裂纹深度关系Fig.9 Relationship between contact stress, sealing width and crack depth

为解释该现象，以1 mm 深度的裂纹为例，密封圈工作接触应力局部分布情况如图10（a）所示；采取同样方法，分别在密封圈无裂纹处接触面、1 mm深裂纹处接触面、5 mm深裂纹处接触面提取11 个节点的工作接触应力数值，如图10（b）所示；裂纹初始状态与加载后的状态对比如图10（c）所示。由图10 可知，在裂纹初期，密封圈裂纹处受压时与毂座的接触状态与无裂纹处相比产生了以下变化：裂纹将密封圈与毂座的接触面分成上、下两个部分，压力载荷的施加使密封圈裂纹处上部结构与下部结构产生偏移，进而上部结构与毂座的接触形成了独立的接触面，在该接触面，最大接触应力相较无裂纹处有所减小，说明裂纹使载荷在接触面处重新分配。最大接触应力位置的上移导致有效密封宽度位置上移。并且，裂纹越深，上部结构与下部结构产生的偏移越明显，导致上部结构与毂座的接触越均匀，接触应力极值越小，有效密封宽度越大。

图10 有裂纹密封面接触情况Fig.10 Contact situation of sealing surface with a crack

（2）裂纹位置对密封性能的影响

取裂纹距节点10的距离为裂纹位置，采取的裂纹位置为0 mm、0.5 mm、1 mm 和1.5 mm，得到裂纹在不同位置时的节点3处接触应力与有效密封宽度的变化趋势如图11所示。对比1.2节密封标准，预紧工况与工作工况的有效密封宽度均符合不小于2 mm 的要求。且裂纹距节点10的距离为0.5 mm 时接触应力与密封宽度最小，最容易产生密封失效。将图7（c）局部放大，如图12所示，无裂纹密封圈工作工况受到的最大等效应力中心距节点10 的距离为0.5 mm，裂纹最容易在此处产生，验证了计算结果的合理性。

图11 节点3接触应力、密封宽度与裂纹位置关系Fig.11 Relationship between contact stress, sealing width and crack position

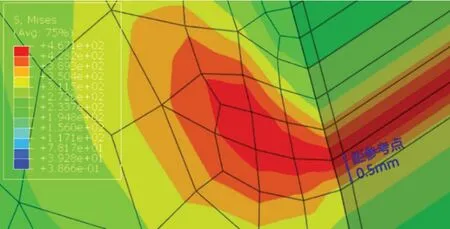
图12 无裂纹密封圈的最大等效应力位置Fig.12 Maximum Mises position of sealing ring without crack

（3）裂纹角度对密封性能的影响

取裂纹与接触面的夹角为裂纹角度，采取的裂纹角度为30°、60°、90°、120°和150°，得到不同裂纹角度时的节点3处接触应力与有效密封宽度的变化趋势如图13所示。对比1.2节的密封标准，预紧工况与工作工况的有效密封宽度均符合不小于2 mm的要求。且裂纹角度为90°时接触应力与密封宽度最小，密封圈最容易密封失效。图14 同样为图7（c）的局部放大图，无裂纹密封圈工作工况受到的最大等效应力范围与接触面大致呈90°角，裂纹最容易在该角度产生，说明了计算结果的合理性。

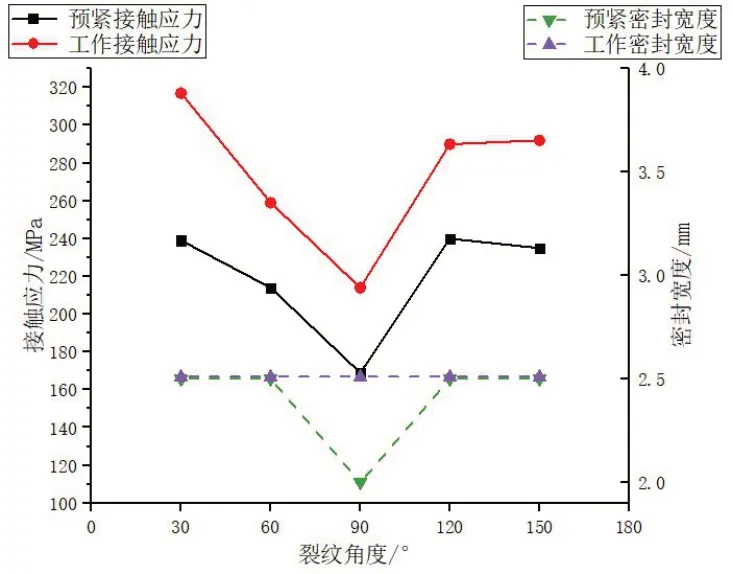
图13 节点3接触应力、密封宽度与裂纹角度关系Fig.13 Relationship between contact stress, sealing width and crack angle

图14 无裂纹密封圈的最大等效应力角度Fig.14 Maximum Mises angle of sealing ring without crack

（4）有限元计算结果与理论值的对比

以裂纹深度为0.5 mm、裂纹距节点10 的位置为0.5 mm、裂纹角度为90°的裂纹为例，图15 为两种工况下密封面上接触应力通过有限元软件的计算值与第2 章理论公式的计算值的对比图。由图可知，两种工况下接触应力的理论值与有限元计算值的总体变化趋势基本一致，均随着预紧力、工作内压的增大而增大。然而，随着预紧力、工作内压增大到一定程度，接触应力有限元计算值的增幅渐缓。这是因为密封面上有效密封宽度逐渐增大，导致接触应力出现增幅减缓的趋势。在两种不同工况下，接触应力最终的有限元计算结果和理论计算结果的误差分别为18.6%和11.6%。

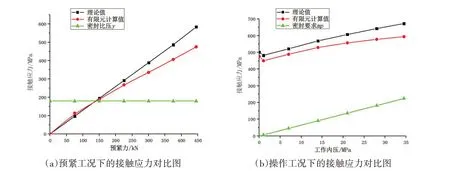
图15 接触应力对比图Fig.15 Comparison of contact stress

4.3 裂纹对密封圈结构性能的影响

在不同裂纹深度、位置和角度下，提取密封圈预紧工况与工作工况的最大等效应力与最大塑性变形如图16所示。由图16（a）可知，预紧、工作工况的最大等效应力、最大塑性变形均随裂纹深度的增加而变大，说明裂纹的扩展让密封圈结构性能变得更加危险；由图16（b）可知，预紧、工作工况的最大等效应力、最大塑性变形在裂纹与节点10的距离为1 mm时最大，与前节结果相差0.5 mm，说明裂纹位置对密封性能与结构性能的影响存在差异；由图16（c）可知，预紧、工作工况的最大等效应力、最大塑性变形在裂纹与接触面的夹角为90°时最大，密封圈最容易结构失效，与前节结果一致。并且，有裂纹密封圈预紧、工作工况的最大等效应力与最大塑性变形相较3.4 节无裂纹密封圈的应力、应变值有所增大，位置都出现在密封圈与毂座的接触面上的裂纹处，表明裂纹的产生使密封圈结构性能更加危险。

图16 结构性能与裂纹深度、位置、角度的关系Fig.16 Relationship between structure performance and crack depth,position,angle

5 结 论

为了揭示水下连接器密封圈预置裂纹故障的密封性能影响成因，本文分别对无裂纹和有裂纹密封圈进行了有限元分析，研究了不同的裂纹深度、位置、角度对密封圈密封性能与结构性能的影响，并将理论推导结果和有限元计算结果进行了对比，得到的主要结论如下：

（1）水下连接器金属密封圈在工作时，与毂座的接触面为应力集中区域，且处于塑性变形状态，容易产生横向裂纹。

（2）裂纹深度越深，密封圈接触面节点3处接触应力与密封宽度越大；裂纹距节点10为0.5 mm 时节点3 处接触应力与密封宽度最小；裂纹角度为90°时节点3 处接触应力与密封宽度最小。但有效密封宽度始终满足要求，裂纹前期对密封圈密封性能影响不大。

（3）裂纹深度越深，密封圈最大等效应力值、最大等效塑性变形量越大；裂纹距节点10为1 mm 时最大等效应力值、最大等效塑性变形量最大；裂纹角度为90°时最大等效应力值、最大等效塑性变形量最大。且相较无裂纹密封圈，有裂纹密封圈的应力、应变极值有所增大，位置在裂纹尖端处，长期使用会导致裂纹扩展，从而使结构断裂，密封发生失效。