一种计及波激振动的船舶结构疲劳损伤的计算方法

乐京霞，李建锋，郭宇龙

(1.武汉理工大学 交通学院，武汉 430063；2 上海船舶运输科学研究所，上海 200135)

0 引 言

随着船舶尺度越来越大，以及高强钢在船舶建造中的应用，船体刚度越来越低。随着船体梁刚度的降低，船体一阶固有频率或其倍频会越来越接近遭遇波浪频率，因此会产生明显的波激振动现象（Lijima 等（2008）[1]；Pedersen 和Jensen（2009）[2]；汪雪良等（2012）[3]）。波激振动现象增大了船体结构应力响应幅值和循环次数，对船体结构疲劳安全产生十分严重的影响。

针对这一问题，国内外许多学者进行了研究。Drummen等（2008）[4]对一艘集装箱船在顶浪中由波激振动产生的疲劳损伤进行了模型试验和数值计算研究，结果表明波激振动产生约40%的总疲劳损伤。Kahl 等（2013）[5]用半经验法评估了在北大西洋和北太平洋航行的集装箱船因波激振动而产生的累积疲劳损伤，发现在两个不同海域下由高频载荷贡献的疲劳损伤分别占总损伤的37%和57%。张弛等（2015）[6]对一艘江海直达船的垂向弯矩进行了模型试验和数值模拟研究，结果表明波激振动和砰击颤振对该船组合垂向弯矩的贡献率超过50%。杨鹏等（2016）[7]对一艘大型油船和一艘大型散货船进行了波激振动模型试验研究，发现在压载顶浪工况下高频弯矩对总累积损伤的贡献占23%～72%。张志康等（2019）[8]基于三维线性频域水弹性理论和刚体理论对一艘18 000TEU 集装箱船进行了疲劳研究，发现波激振动造成结构疲劳寿命普遍下降30%～40%。王伟飞等（2019）[9]研究了波激振动对一艘超大型集装箱船的疲劳损伤影响，发现考虑波激振动时船舶的疲劳寿命会极大地降低,甚至可达50%以上。

总的来看，波激振动现象引起的船体结构疲劳损伤在总的疲劳损伤中有很大的占比，因此能够准确地预报考虑波激振动的船体结构疲劳寿命是有必要的[10]。目前，船舶疲劳损伤评估的谱分析法理论清晰，结果精度较高，是一种较为成熟的计算方法。但是需要耗费大量的时间与计算资源，所以寻找一种效率更高且可靠的方法来解决上述存在的问题，具有重要的工程意义。而设计波法具有工作量小、计算方便的优点，但其在船舶航行工况以及波激振动效应上考虑得不够全面，导致结果精度较谱分析法要低。本文基于传统的设计波法，考虑波激振动对船舶疲劳损伤的影响，提出了一种计及波激振动的船体结构疲劳损伤计算方法。用此方法对一艘集装箱船进行疲劳损伤计算，并将计算结果与谱分析法和模型试验下的结果进行了对比。研究本文提出的疲劳损伤计算方法的合理性与可靠性，为同类船舶疲劳评估提供一种高效可靠的方法。

1 计及波激振动的设计波法

设计波法是给定一个确定参数的典型规则波，例如波高和周期等，并将其作用于船体上，使按它计算出来的船体结构应力范围能够代表实际船体航行过程中一定超越概率水平的应力范围，在此基础上分析结构安全问题。一般确定设计波的途径是对船体波浪载荷进行长期预报，得到规定超越概率水平或重现期的船体弯矩、扭矩等具有代表性的主要载荷参数值，然后依此选择典型的规则波，使之产生与长期预报值相等的波浪载荷。

1.1 设计波法原理

设计波方法认为船舶航行时遭遇各种波浪载荷，考虑以其中最有影响的载荷参数（主要载荷参数）来建立用于船体结构分析的计算载荷组合。即当主要载荷参数达到最大值时，其他载荷取为相应的瞬时值。目前ABS（2014）、BV（2017）、DNV（2015）等[11-13]规范均给出了推荐的主要载荷参数，DNV（2015）[13]提出的几个主要载荷参数为：船舯横剖面最大波浪诱导垂直弯矩、最大水平弯矩、最大扭矩、首柱最大垂向加速度和在船舯剖面附近板格的最大波动压力。ABS（2014）[11]中考虑的主要载荷参数有:垂向波浪弯矩（VBM）、垂向波浪剪力（VSF）、水平波浪弯矩（HBM）、水平波浪剪力（HSF）和扭矩（TM）。实际上主要载荷参数不同，其考察的结构构件的侧重点是不同的。一般情况下他们有一定的对应关系，其关系见表1。

表1 主要载荷参数与评估构件的对应关系Tab.1 Dominant load parameters and corresponding structural members

确定主要载荷参数后，在各选定工况下，计算船舶在不同浪向下的载荷幅值响应算子(RAO)以及载荷的长期值。需要注意的是：计算中应考虑到各个浪向角和足够的波频范围，对计算的主要载荷参数的幅值响应算子，在浪向和频率范围内进行搜索，其中幅值响应算子最大值对应的浪向和频率即为设计波的浪向β和波频ωp。

传统的设计波法通过式（1）来确定波幅

式中，aw为设计波的波幅，Rmax为主要载荷参数的长期预报值，RAOmax为主要载荷参数幅值响应算子的最大值。

1.2 计及波激振动的设计波参数

目前数值分析方法是最常用的波浪载荷计算方法，即运用波浪载荷计算软件得到波浪载荷，但由于波浪载荷的复杂性，其在计算过程中并不能完全考虑波激振动对波浪载荷的影响，而波激振动对船舶遭受的波浪载荷有很大的贡献，这也就导致预报的波浪载荷相对实际是偏小的。由此确定的设计波产生的波浪载荷相对于实船受到的波浪载荷相差较大，从而导致对船体结构疲劳损伤的评估相对偏小。为了更好地评估船体结构疲劳损伤，本文提出了一种计及波激振动的设计波法。在本方法中，主要载荷参数、设计波浪向β和波频ωp的确定与传统的设计波法一样；但在确定设计波的波幅时，引入了一个修正系数μ，将数值分析计算中未考虑到的由波激振动诱发的载荷成分通过修正系数μ叠加到设计波的波幅中。修正系数μ的计算如式（2）所示，设计波的波幅计算如式（3）所示式中，RAOSmax为实船波浪载荷RAO最大值，RAONmax为数值分析计算的波浪载荷RAO最大值。

确定修正系数μ中的关键问题在于如何获取实船的波浪载荷RAOSmax，目前可以通过实船测量和模型试验获取波浪载荷。本文通过弹性模型试验来测量模型受到的波浪载荷，通过相似转换获取实船的波浪载荷。

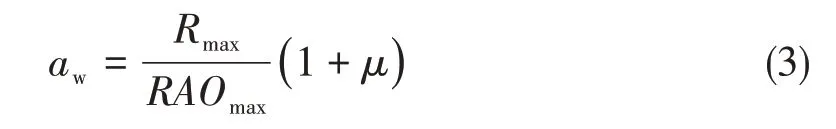
式中，μ为修正系数，表示波浪载荷在数值分析中未预报部分占比。

计及波激振动的设计波参数计算流程如图1所示。

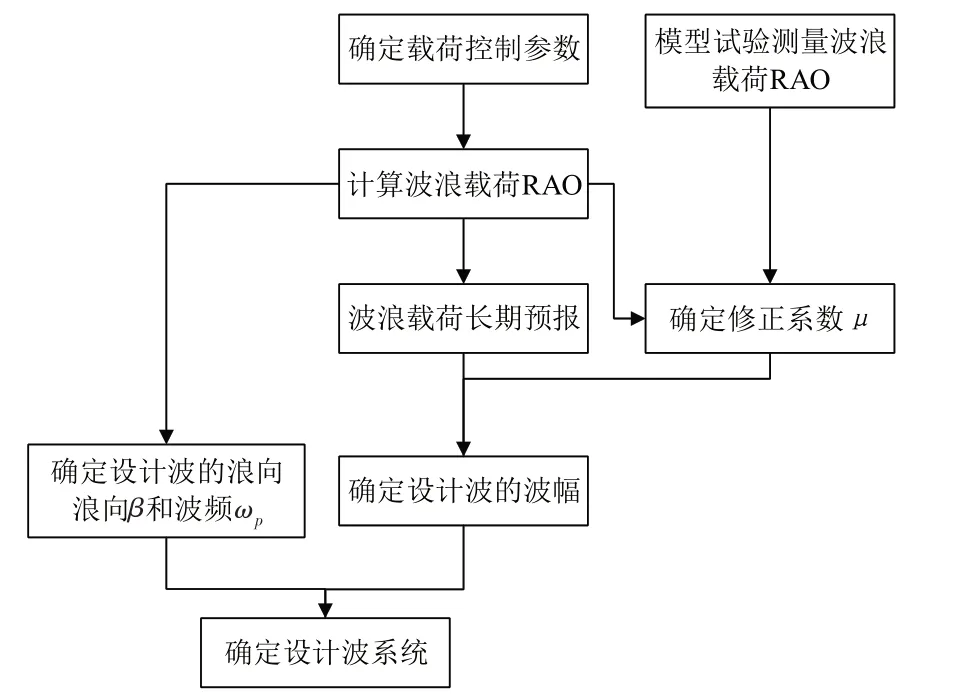
图1 计及波激振动的设计波参数计算流程图Fig.1 Calculation flow chart of design wave parameters considering springing

2 计及波激振动的设计波参数确定

2.1 波浪载荷RAO

本文以一艘无限航区内的260 m集装箱船作为目标船舶进行计算，其主尺度如表2所示。船舶的固有频率利用有限元软件MSC/Patran 计算获得，船舶前两阶垂向弯曲振动的固有频率如表3所示，模态振型如图2所示。在波浪载荷预报中，将船体考虑为弹性体，在三维波浪载荷软件Hydrostar 的弹性模块中对船舶的波浪载荷进行计算，在计算中需要建立船体的水动力模型。水动力模型包括湿表面模型和质量模型，湿表面模型即浸没在水中的船体外壳板元模型。质量模型是在湿表面模型的基础上输入船舶实际的质量载荷分布，用于统计船舶整体重量、重心分布和回转半径等稳性参数，水动力模型如图3。

表2 集装箱船主尺度Tab.2 Main dimensions of container ship

表3 船舶前两阶垂向弯曲振型和固有频率Tab.3 First two vertical bending modes and natural frequencies of the ship

图2 船舶二节点和三节点垂向弯曲模态振型Fig.2 Vertical bending mode shapes of the ship with two and three nodes

图3 水动力模型Fig.3 Hydrodynamic model

本文研究对象为甲板、横舱壁及舱口围板等构件，根据表1选取船舯剖面垂向弯矩(VBM)作为设计波的主要载荷参数。在频域范围内考虑波激振动，对船体进行水动力分析，计算中仅考虑了线性波激振动，计算航速为服务航速11.88 m/s。为了考虑到船舶所有可能遭遇的浪向以及足够的频率范围，浪向角的选取范围为0°(随浪)～360°，步长为45°；波浪频率的选取范围为0.2～1.5 rad/s，步长为0.1 rad/s。计算后得到船舯剖面垂向弯矩的RAO结果，如图4所示。从计算结果可以看出，不同浪向下的舯剖面垂向弯矩RAO峰值的频率均在0.55 rad/s附近，通过公式（4）将其转换为遭遇波频率，与1/4倍船舶二节点垂向弯曲固有频率0.87 rad/s接近，且从图中可以看到在高频波浪区域（＞0.8 rad/s），多个浪向下的垂向弯矩响应峰值较为明显，分别位于遭遇波频率1.7 rad/s及2.8 rad/s附近，接近低频峰值的2倍和3倍。

图4 船舯剖面垂向弯矩RAOFig.4 RAO of VBM

式中，ωe为遭遇波频率，rad/s；ω为波浪频率，rad/s；g为重力加速度，m/s2；V为航速，m/s；β为浪向角，随浪时为0°，迎浪时为180°。

2.2 长期预报

长期预报旨在用统计的方法确定波浪载荷在一定超越概率下的极值，其可被视为由一系列各自独立的短期预报组成。波浪载荷的长期预报值是各短期预报值和浪向概率分布的加权组合，如式（5）所示：

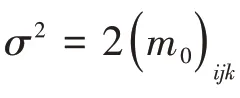
船舶一生遭遇的波浪载荷循环次数约为N=108，与常用船舶设计寿命周期25 年来确定极端海况的概率水平接近，故本文将超越概率取为Q=1/N=10-8。长期预报也需要给定航行海域内波浪的长期统计资料，本文计算的是一艘无限航区的远洋船舶，选用DNV（2015）[13]推荐的全球波浪散布图。

2.3 实船波浪载荷RAO的预报

实船波浪载荷RAO的预报是通过弹性船模试验来实现的，试验测量得到船模的波浪载荷，通过相似准则可以换算得到实船的波浪载荷，最后将实船波浪载荷单位化即可得到实船波浪载荷RAO。

本次试验的目的是得到船模的垂向弯矩，实际是通过应变片测量得到船模结构的应变，再将应变数据转换为垂向弯矩，因而最终需要确定垂向弯矩M及应变ε之间的关系。

在船模中，龙骨梁可看作为一根单跨梁，其截面垂向弯矩和应力满足式（6）：

应力与应变之间的关系为

将式（7）代入式（6），并考虑到测量误差，可得到截面垂向弯矩与应变呈线性关系，

式中，K1=EIz/y是一个关于材料弹性模量E及龙骨梁截面惯性矩Iz的数，一旦龙骨梁模型确定，对于各截面而言K1即为常数；K2为常数，主要包含了误差项。

在实际试验中，可以用如下方法获得截面垂向弯矩与应变的关系：将船模龙骨梁取出，固定其两端，构建一个两端简支的单跨梁系统，并在梁上悬挂重物，模拟集中力加载，采集应变数据。同时根据分析得到龙骨梁截面应力理论值，联立两者即可得截面垂向弯矩与应变的关系，如图5所示。

图5 垂向弯矩与应变关系确定流程图Fig.5 Flow chart for determining the relationship between VBM and strain

船模的设计应满足几何相似、重力相似（Froude 数Fn相等），惯性力相似（Strouhal 数St相等）以及流体动力相似（Euler 数相等）[14]，可以通过式（9）将船模垂向弯矩RAOm换算得到实船垂向弯矩幅值响应算子RAOS：

式中，Λ为实船与船模缩尺比；RAOm为船模垂向弯矩幅值响应算子，kN·m/m；RAOS为实船垂向弯矩幅值响应算子，kN·m/m。

根据上述试验原理，在武汉理工大学拖曳水池进行试验，基于各相似准则以及试验场地情况对260 m集装箱船模进行设计，确定船模的缩尺比Λ为64。船模采用分段龙骨梁型玻璃钢拖航船模，沿船长方向一共平均分为8段，用一根变截面龙骨梁将各分段连接，各分段连接处截面由船尾到船首依次编号为1～7。试验中在中间5 个截面处（2-6 号截面）龙骨梁上布置应变片用以测量截面处的应变，分段模型如图6所示。

图6 分段模型Fig.6 Segmental model

本次模型试验共进行了8 组迎浪下的规则波试验，航速为1.49 m/s，对应实船服务航速11.88 m/s；试验的具体工况如表4所示。

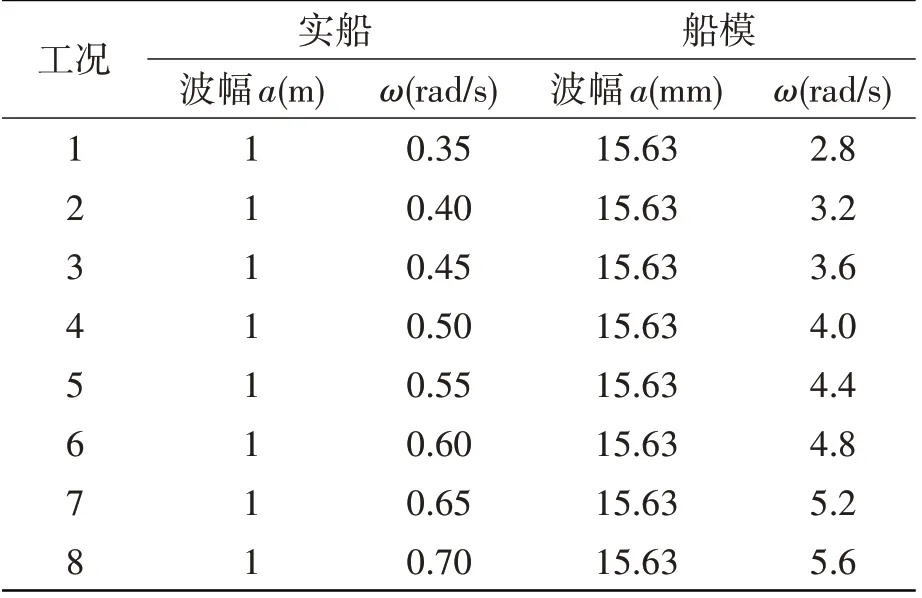
表4 试验工况Tab.4 Test conditions

通过试验测量得到各工况下船模各截面的垂向弯矩时历值，取其峰值作为截面垂向弯矩统计值，根据式（9）换算为实船的垂向弯矩RAO，并将波浪频率转换为遭遇波频率，如图7 所示。发现各截面垂向弯矩的峰值对应的遭遇波频率均接近1/4倍船舶二节点垂向弯曲固有频率，且在试验过程中观察到船舶有明显的波激振动现象。

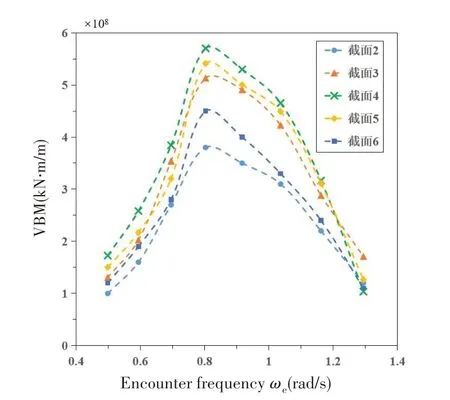
图7 各截面垂向弯矩RAOFig.7 RAO of each section’s VBM

2.4 设计波参数确定

根据2.2节的计算结果，对船舯剖面垂向弯矩RAO，在所有浪向和频率范围内进行搜索，发现当浪向角为180°时，舯剖面垂向弯矩RAO出现最大的峰值，峰值对应的波浪频率为0.57 rad/s，即可确定设计波的浪向β=180°和波频ωp=0.57 rad/s。

将迎浪状态下的试验与数值分析的船舯剖面垂向弯矩RAO进行对比，试验中即截面4 垂向弯矩RAO，如图8 所示。图8 中试验和数值分析的第一个峰值是由船波耦合产生，而在数值分析中，在高频区还出现了峰值，这个峰值对应频率1.7 rad/s接近船舶二节点垂向弯曲固有频率的1/2倍，因此推测船舶是由波激振动现象产生的；还可以发现舯剖面垂向弯矩RAO的试验峰值要比数值分析峰值大，超出的弯矩部分可由波激振动和砰击响应贡献，而本文试验中并没有出现砰击现象，且在数值分析中仅考虑了线性波激振动，因此可以推测试验比数值分析多出来的垂向弯矩是由非线性波激振动贡献。且从图中可以得到实船舯剖面垂向弯矩RAO最大值RAOSmax和数值分析预报的RAO最大值RAONmax，代入式（2）可得到船舯剖面垂向弯矩在数值分析中未预报部分占比，即修正系数μ。最后将长期预报值Rmax、船舯剖面垂向弯矩RAOmax和修正系数μ代入式（3）即可得到设计波的波幅。由此计及波激振动的设计波参数全都确定，如表5所示。

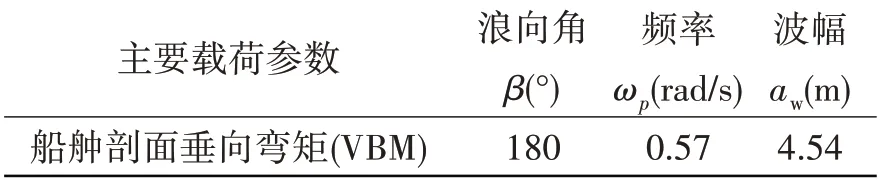
表5 设计波参数计算结果Tab.5 Calculation results of the design wave parameters

图8 试验与数值仿真的船舯剖面垂向弯矩RAOFig.8 RAO of VBM by test and numerical simulation

3 累积损伤计算

3.1 设计波法计算疲劳损伤

用设计波法计算结构累积损伤时，可以认为船舶设计寿命期间应力范围S的长期分布为瑞利分布，考虑到Nload个装载工况，使用DNV（2015）[13]规范提供的S-N曲线，则累积损伤D可以由式（10）计算：

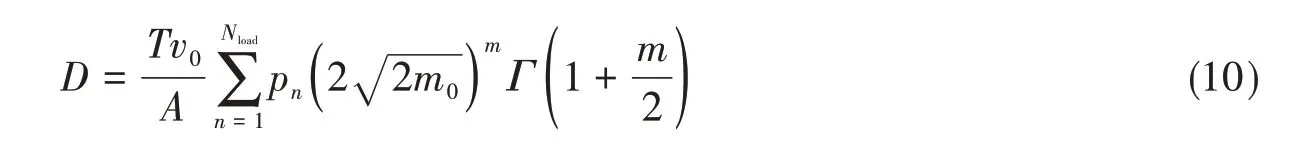
式中，m、A为S-N曲线的两个参数，本文取m=5，A=15.606；T为船舶设计寿命，本文取25 年；v0为应力响应的长期平均过零率；Nload为装载工况数；pn为第n个载况所占设计寿命的比例，根据实船生命周期各种载况的分配比率确定，如无法获取，可假定各载况时间为平均分配；m0为应力响应谱的零阶矩；Γ( )为伽马函数。下文出现相同符号表示相同含义。

在模型试验中，计算结构累积损伤时，可以认为船舶设计寿命期间应力范围S的长期分布为瑞利分布，考虑到Ncase个试验工况，使用DNV（2015）[13]规范提供的S-N曲线，则累积损伤D可以由式（11）计算：

式中，Ncase为试验工况数；pc为第c个试验工况所占设计寿命的比例，本文各工况发生的概率相同，取为0.125。

3.2 谱分析法计算疲劳损伤

根据Miner 的线性累积损伤理论，疲劳损伤是由一系列不同应力幅值的循环载荷引起的，用各短期分布累积损伤度的组合得到，考虑Nload个装载状态，使用DNV（2015）[13]规范提供的S-N曲线，则累积损伤D可以由式（12）计算得到：

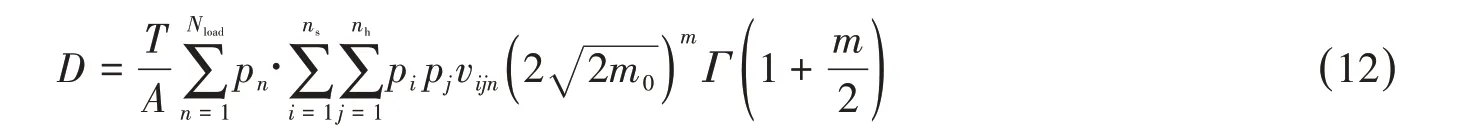
式中：ns为所有海况数；nh为所有航向数；pi为第i个海况出现的概率；pj为第j个航向角出现的概率；vijn为第n个装载工况及第i个海况第j个航向角下，应力响应的平均过零率。

3.3 有限元模型

本文结构应力在有限元软件MSC/Patran 中完成，260 m集装箱船的有限元模型如图9所示，通过板、梁及杆单元模拟其有效承载构件。依据规范建议的疲劳寿命校核位置，选取了六个点作为疲劳分析时的热点，热点详情如图9和表6 所示。在热点处进行模型细化处理，以尽可能接近真实情况，模型的细化准则依照DNV（2015）[13]规范中的要求：最小网格尺寸为板厚，范围为10 倍板厚，并沿热点周围依次延伸至正常网格；热点处应力以线性插值为准，插值点取在距热点t/2和3t/2处。

表6 疲劳损伤计算热点Tab.6 Hot spots of fatigue damage calculation

图9 全船有限元模型及热点位置Fig.9 Finite element model and hot spot location of the whole ship

3.4 疲劳损伤计算及分析

基于上述三种疲劳损伤的计算方法，计算热点的累积损伤值，计算结果如图10所示。

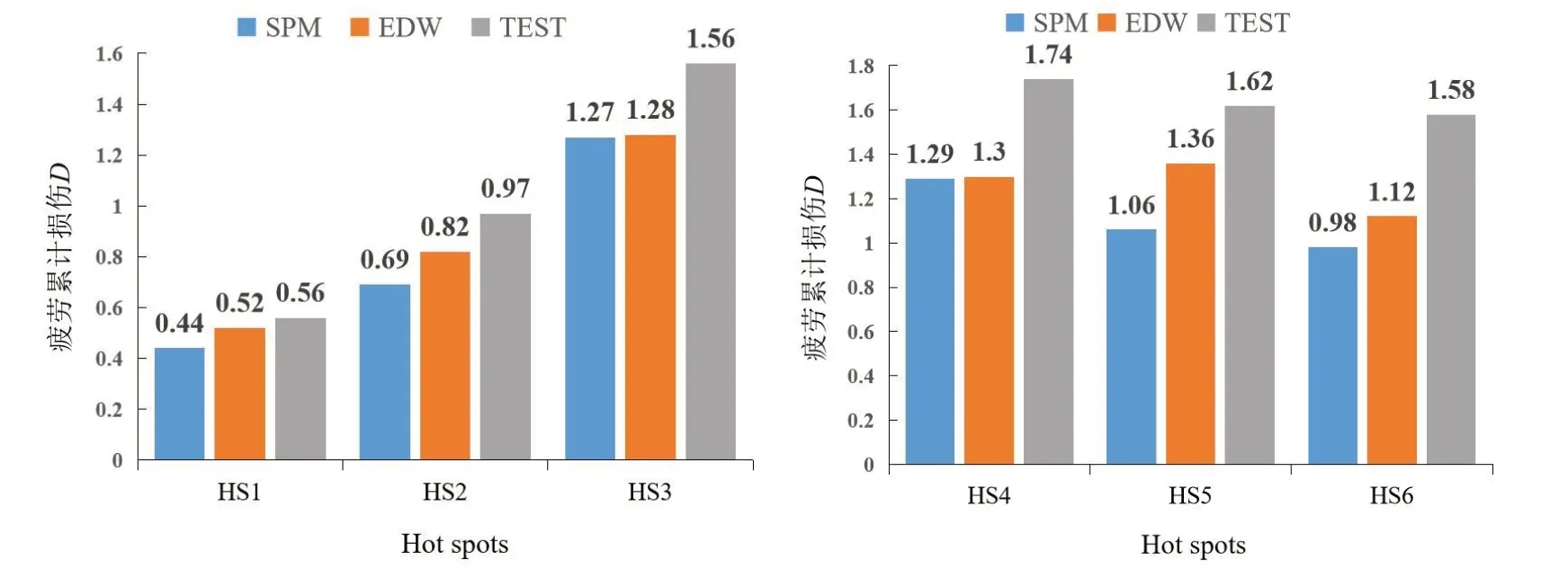
图10 热点的累积损伤计算结果Fig.10 Cumulative fatigue damage of hot spots

通过对比谱分析法（SPM）计算而得到的累积损伤值与设计波法（EDW）的结果可知，设计波法计算结果普遍较谱分析法大，且两者均比基于试验数据（TEST）的结果小。以热点HS5而言，该热点位于船中截面内底板上，船中受到的弯矩最大，且内底板受总纵弯矩的影响很大，因而累积损伤预报效果最佳；同样，其余热点，如HS1、HS2、HS6也均存在不同程度的类似效果。这也表明了本文提出的方法对船舶疲劳损伤的预报有一个很好的效果。对于热点HS3 和HS4，设计波法和谱分析法计算的累积损伤值相近。这是由这两个热点的位置确定的，热点HS3和HS4均在主甲板舱口角隅的加强区内，该区域内板厚很大，厚度均在60 mm左右，远超其他板厚范围（8～15 mm）。导致此处结构局部刚度较大，其对波浪弯矩的响应不敏感，在用设计波法计算时也未考虑刚度影响，故设计波法对热点HS3和HS4的累积损伤的预报效果不佳。但就整体而言，相比于谱分析法，设计波法的计算结果更接近试验结果，可以认为用计及波激振动的设计波法能得到一个更为合理可靠的累积损伤结果，为船舶设计初期的疲劳寿命预估提供了参考。

4 结论与展望

4.1 结论

波激振动现象大大降低了船舶的疲劳寿命，因此能够准确高效地预报考虑波激振动的船体结构疲劳寿命是有必要的。本文提出了一种计及波激振动的设计波法，对一艘260 m 集装箱船进行疲劳分析，并将结果与模型试验和谱分析法计算的结果进行比较分析，得到如下结论：

（1）在模型试验与数值分析中都发现船舶在波浪运行中有明显的波激振动现象，因此在进行船体结构疲劳分析时需要重视波激振动的影响。

（2）通过试验与数值分析预报得到的船舯剖面垂向弯矩对比，发现数值分析的预报值比试验值小很多，不能完全考虑波激振动对船体结构的影响，严重影响了船舶疲劳寿命的评估。

（3）相较于谱分析法，本文提出的计及波激振动的设计波法得到的累积损伤结果更加符合试验结果，说明本文提出的计算方法是合理可靠的，可以为同类型船舶提供一种高效且可靠的结构疲劳评估方法。

4.2 展望

（1）实际船舶的航行周期内，往往存在多种装载工况及航速的组合，在每种不同组合下都会影响船体的波激振动响应，对最终的船体结构累积损伤计算均有一定影响。但本文仅考虑了一个装载工况及航速下的船体结构响应，后续需要对不同装载工况组合进行研究。

（2）从现有的研究中可以发现，非线性成分对疲劳寿命也存在影响，但本文研究范畴仅限于线性部分，加上水池造波条件的限制，并没有进行非线性波激振动对疲劳寿命的影响研究。

（3）本文提出的方法目前仅适用于规则波下的船体结构疲劳评估，对于不规则波下的疲劳评估还需进一步的研究和验证。