多浮体耦合的长大过江弯管系统沉放过程动力响应数值仿真分析

方一如，林平均，巫志文，农 站，肖扬洋

（1.广西大学 a.土木建筑工程学院;b.工程防灾与结构安全教育部重点实验室，南宁 530004；2.广西建工集团建筑工程总承包有限公司，南宁 530000；3.广西防灾减灾与工程安全重点实验室，南宁 530004）

0 引 言

沉管法[1]是将若干个预制段分别浮运到海面（河面）现场，并逐一按序沉放安装在已疏浚好的基槽内，以此完成水下管道修建的施工方法。沉管法具有施工质量高、造价低、工期短、适用水深范围广等优点。近年来沉管法在国内外得到了广泛的使用和快速发展，被大量地应用于沉管隧道、海洋输油管道、过江管道等工程结构的水下沉放安装施工中。水下管道沉放施工过程涉及很多关键技术，如沉管管段的浮运和沉放、管道的定位、管段的连接等。其中，管道沉放是整个管道水下施工中极为重要和关键的一环，在水动力环境条件下，沉管管道在沉放过程中的运动响应直接影响管道施工过程的安全性和稳定性、水下定位的精度和施工的经济性等[2-4]。而且，管道通常具有体积大、重量大、施工作业环境复杂等特点，管道沉放过程工艺复杂，涉及到人员、设备、拖船等的统筹安排，控制不当极易导致施工事故，造成重大的人员财产损失。此外，如果施工安排不够科学合理，极易造成燃油、人力资源、设备的极大损耗，同时影响施工的进度。

国内外学者和工程师通过理论分析、数值模拟、模型试验、现场实测等手段，对沉管隧道、海洋输油管道、过江管道等工程结构沉放施工过程的动力响应展开了广泛深入的研究[5-7]，形成了丰富的理论、数值及试验或现场实测方面的研究成果。

理论和数值研究方面，伦冠德等[8]以空间大变形梁理论为基础建立了海底管道提吊及沉放的有限元模型，研究了纵向水流、侧向水流及海床摩擦作用下管道提吊及沉放过程中的管道形态及应力分布；王智强等[9]以港珠澳大桥沉管管道工程为背景，利用三维势流理论，通过ANSYS 软件建立超长沉管管道沉放过程的数值模型，用AQWA 软件对其进行频域和时域的分析，为沉管沉放提供施工建议；于孝民等[10]利用理论分析研究了大直径长距离输水钢管整体沉放可控浮箱和支撑吊装平台系统施工工艺技术。

试验和现场实测研究方面，陈智杰等[11]以港珠澳大桥沉管隧道沉放工程为背景，通过试验手段，研究了波浪作用下沉管管道沉放过程的运动特性；Xiao 等[12]通过模型试验，对跨越甬江的过江沉管管道的沉放安装过程进行了水动力分析，得到了沉管管道在拖曳-沉放过程中系泊载荷和吊缆张力的变化特性；左卫广等[13]通过物理模型试验，研究了不规则波作用下单驳船沉放过程沉管管道的动力响应问题，采用Welch 方法对沉管管道动力响应进行了频谱分析，并探讨了不同波浪周期和波高情形下的沉管管道运动和缆绳张力的频谱特性。

在试验和现场实测与数值模拟相结合方面，詹德新等[14-15]以南京沉管隧道为背景，通过物理模型试验，研究了四浮筒沉放条件下沉管管道浮运和沉放过程中的流体作用力及吊放缆绳张力特性，并建立了管道的水面浮运及沉放过程数学模型；Cozijin 等[16]通过数值模拟和现场测试相结合的方法，研究了波浪要素对韩国釜山－巨济岛沉管隧道在沉放过程中沉管管道运动响应的影响；应宗权[17]等针对广州洲头咀沉管隧道工程，通过ANSYS 建立了管道的三维实体模型，并与现场实测相结合，对沉管隧道管道沉放过程中缆力与运动响应进行了分析。

从目前研究现状看，对于工程结构沉放施工过程的动力响应研究已经较为成熟，极大地促进了沉管结构的工程应用。但是，目前研究的对象多属于规则直线型的沉管结构，考虑多体耦合[18-19]的研究也较少。在某些特殊情况下，譬如由于水底基槽地形的限制，需要将沉管做成弯曲的形式，弯曲型沉管的受力机理和直线型明显不同，由于其不规则的结构形式，更容易导致其在水域环境的沉放过程中存在沉管及其缆索受力不均匀、管体局部应力集中、受力复杂等问题。更值得引起注意的是，为了保证施工的安全性，通常都需要为其配备多浮体（例如钢浮筒、气囊、驳船等）的沉放系统。由于多浮体系统的存在，浮体与锚泊系统的耦合、浮体与浮体的耦合、浮体与流体之间的流固耦合，组成了非常复杂多浮体耦合系统。多浮体耦合的长大弯管系统沉放过程，安全控制难度极大，控制不当极易导致缆索破断、驳船倾覆、管道麻花状扭断、管道侧翻、沉放不到位等工程事故。

本文以南宁市邕江过江管道沉管施工为背景，针对多浮体耦合的长大弯管系统沉放过程中的动力响应问题进行研究，研究应用非线性时域动力分析方法、莫里森水动力理论、长大弯管理论等，借助OrcaFlex 软件，建立了考虑多体耦合的长大弯曲型过江管道沉放过程水动力数值仿真分析模型。对影响沉放过程动力表现的关键施工变量，如气囊放气和管道下放的配合、气囊放气时间、吊缆预张力等进行了参数敏感性分析，根据数值模拟结果提出了施工安全性控制技术及施工建议。

1 工程概况

本文模拟的管道工程位于邕江较深的江段，依托南宁邕江过江管道工程，河床地形呈如图1（a）所示的不规则的曲柄型形态，过江管道贴合河床形状设计，沉管管道总长为438 m，分为四段进行预制组装，为目前为止广西境内管径最大、跨度最长的输水管道。图1（b）为施工方案设计的由钢浮筒、气囊、驳船等组成的多浮体耦合沉放系统，沉放系统由过江弯管、江中8艘驳船、两岸2台履带吊组成。管道迎流面布置了9 个气囊，背流面布置了16 个钢浮筒，气囊和钢浮筒通过锚索与管道连接，在沉放前提供浮力以支撑管道悬浮于水中。工程中涉及的具体浮体参数如表1所示。

表1 结构参数表Tab.1 Structural parameters of the immersion system

主要的沉放过程如图1（c）所示：（1）沉放前，管道在钢浮筒和气囊的支撑下飘浮在水面；（2）往管道注满水，使其在压载水作用下浸没并悬浮于水中；（3）打开气囊气阀放气，整个管道受力将由气囊、钢浮筒慢慢过渡到钢浮筒和驳船吊缆，管道随着气囊消气继续下沉。

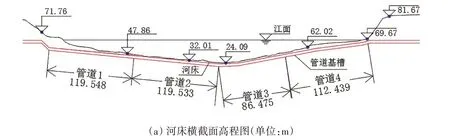
图1 管道沉放过程示意图Fig.1 Schematic diagram of the pipeline in the immersion process

根据施工现场测试确定参数：流速为0.35 m/s；风速为5 m/s；考虑最危险工况，即风流90°同向。

2 数值建模及基本理论

2.1 沉放模型构建

数值模拟使用两种坐标系如图2所示，分别是全局坐标系O-XYZ和局部坐标系o-xyz，其中，O和o分别是全局坐标系和局部坐标系的原点，分别定义在江底和浮体质心处。本文采用考虑非线性时域动力分析方法和多浮体相互作用的全耦合方法，建立数值仿真分析模型，分析沉放过程中浮体动力响应及缆索张力。

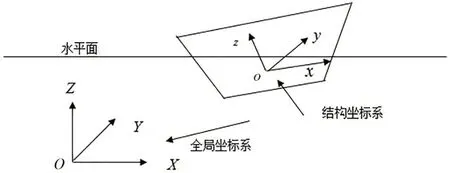
图2 坐标系定义Fig.2 Sketch of the coordinate system

系统中所有浮体均运用6自由度的单元进行模拟，管道、驳船等主要受力构件模型构建过程如下所述。

2.1.1 管道模型

管道模型使用line 单元模块建立，按管道焊接情况建立四段管道，连接处采用刚性连接。模拟管道的line 单元每米划分一个网格，总共438 个网格，管道两端在X和Y方向被约束。建立模型时，在首尾的X和Y向两端各加2个links单元来限制位移，模拟两端约束作用。

基于集中质量法，将管道离散成若干连续线单元，如图3所示，管道质量、重力以及浮力等作用于各个单元节点上，节点之间由无质量的弹簧连接，通过节点和弹簧的受力和变形来体现管道的运动响应，单元中心处的轴向弹簧和扭转弹簧及相应的阻尼器分别模拟管道的轴向和扭转特性，而节点两端处的转动弹簧和阻尼器用来模拟管道的弯曲特性[20]。

图3 线单元模型Fig.3 Line element model

OrcaFlex 依次通过五个阶段计算管道节点内力：（1）轴力；（2）弯矩；（3）剪力；（4）扭矩；（5）总载荷（重力等）。

2.1.2 船舶模型

在过江管道沉放施工的过程中，施工驳船通过吊缆对长大弯管进行起吊作业，船舶模型通过vessel 单元建立，水流作用下驳船和管道将会发生耦合运动，船舶运动响应通常可由AQWA 模拟得到的运动幅值响应函数计算得到，将计算好的驳船六个自由度的运动响应数据按照顺序依次填写到对应的栏目中。

2.1.3 吊缆模型

吊缆连接驳船与管道，吊缆长度在沉放的过程中不停改变，因而需要采用可以实时变化长度的单元来模拟，数值建模中采用winch 单元来模拟实际沉放过程中吊缆的下放。Winch两头的连接点由相对坐标来控制，计算时可通过吊缆伸长量得出吊缆张力。

2.1.4 钢浮筒模型

钢浮筒采用6D Buoys 模块建立，类型为spar，它拥有6 个自由度，为3 个平动自由度和3 个旋转自由度，运行时分开计算每个钢浮筒的浮力。钢浮筒通过line 单元建立的锚缆与管道连接。在此模块建立的每个钢浮筒均被视为刚体，实际工程中钢浮筒仅绕管道运动，所以将钢浮筒连接的锚缆的线单元X方向的抗弯刚度设置为无穷大。

2.1.5 气囊模型

气囊采用shape 单元建立，类型为drawing，放气过程中气囊体积减少，提供的浮力随之减少，在模型中通过设置load force模拟气囊施加在管道上线性递减的力，模拟气囊放气。结合单元生死功能，模拟气囊放气完毕后从管道上脱落。

2.2 数值建模基本理论

过江管道沉放系统各部分的运动控制方程如下：

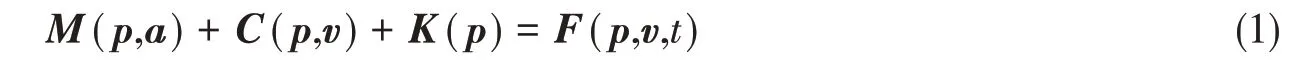
式中，M(p,a)是系统惯性载荷；C(p,v)是系统阻尼载荷；K(p)是系统的刚度载荷；F(p,v,t)是系统外载荷，p，v和a分别是结构位移、速度和加速度矢量；t是模拟时间。

OracFlex 软件主要采用隐式动态迭代方法对系统的动态分析运动方程进行动态计算，上述数值方法在每一时间步长内对系统几何构型进行重新计算，故该数值模拟可以充分考虑几何非线性特征，包括水动力荷载（水流力、风力）和接触力的空间变化。结构的动力响应主要受系统阻尼载荷、系统刚度载荷和外部载荷等因素影响。本研究采用全耦合法对系统运动过程进行求解分析，可以较好地考虑长大弯管几何构型的非线性，管道、钢浮筒和气囊之间的动力耦合作用，以及流固耦合作用等复杂因素影响。通过该运动方程即可获得管道的动力响应，根据各吊点（锚点的位移情况）通过吊缆（锚索）伸长量得出吊缆（锚索）张力。

2.2.1 系统外载荷

数值模拟时需考虑的载荷主要有：重力、浮力、流体力、风力、拖曳时受到的波浪力学附加质量效应、拉力和剪力、弯距和扭矩、吊缆和绞盘的力等。

针对管道及钢浮筒细长浮体结构，一般可以忽略管道对水质点速度和加速度影响，考虑水流共同作用，所受到的水动力载荷，通过扩展形式的莫里森方程考虑：

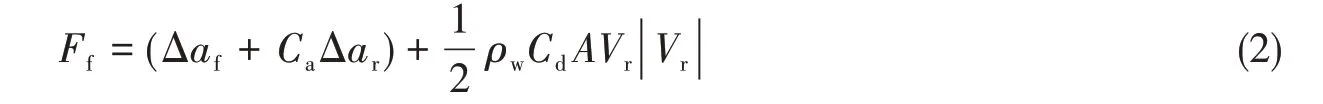
式中，Ff是流体力，Δ是排水量，af是相对于大地的流体加速度，Ca是结构的惯性力系数，ar是相对于结构的流体加速度，ρw是水的密度，Vr是相对于结构的流速，Cd是拖拽力系数，A是阻力面积。其中，结构物各向的拖曳力系数和惯性力系数根据规范DNV-RP-C205[21-22]和《港口工程荷载规范》(JTS 144-1-2010)[23]取值，其余参数依据施工方案和现场实测确定。

对于管道、钢浮筒、气囊、驳船等浮体结构，其在三个坐标轴方向上受到的风力分别为

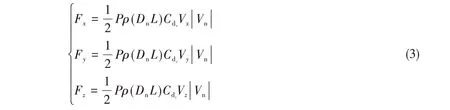
式中，P为迎风面积比例系数；ρ为空气密度；Dn为法向阻力/升力缆索直径；L为缆索单位节段长度；Cdx、Vx、Cdy、Vy和Cdz、Vz分别为结构在(x,y,z)方向的拖曳系数和风相对结构在该方向的相对速度的分量；Vn为风相对结构速度的法向分量。

类似地，对于缆索等小尺度结构物，其在三个坐标轴方向受到的风力计算方式如下：

式中，Da为轴向阻力/升力缆索直径,V为风相对结构的相对速度。

2.2.2 系统阻尼载荷

计算管道、钢浮筒、驳船等浮体的附加阻尼和阻尼刚度时，阻尼载荷的计算采用下列方程：

式中，V是相对于全局参考系原点的浮体速度和角速度(6自由度)，D是指定的阻尼载荷。计算细节具体见OrcaFlex Manual[20]。

3 数值仿真计算及结果讨论

施工现场环境如图4所示（现场布置可能因实际情况而变动），数值模型鸟瞰图见图5。建立模型后，为进行施工安全性控制，选取三个关键的施工变量进行研究，分别是分析气囊放气与管道下放是否应配合、气囊放气的速度、吊缆的预张力，如表2所示。

图4 现场施工示意图Fig.4 Diagram of the construction site

图5 数值模型鸟瞰图Fig.5 Aerial view of the numerical model

表2 计算工况表Tab.2 Calculation cases

3.1 典型工况的时域分析

数值模拟中考虑选定放气的同时下放管道，放气30 s，吊缆施加5 kN的预张力的施工条件组合作为典型工况，通过计算分析其在沉放过程中的钢浮筒锚缆受力、驳船吊缆受力、管道六自由度动力响应，以及管道沿长度方向的受力等。

3.1.1 沉放过程中钢浮筒锚缆受力

图6 为沉放过程中锚缆受力的时域曲线，其中图6（a）～（c）分别为1 到16 号锚缆缆力的时域曲线图，图6（d）为各锚缆受力最大值对比图。从图6（a）～（c）可以看出，1号到16号锚缆的缆力时域曲线走势均比较相似，基本上表现为：缆力在0～10 s之内缓慢增加，10～30 s急剧增加，而在30 s后收敛于恒定值。从图6（d）中可以看出，沉放过程中钢浮筒锚缆的受力大体均匀，相对差值一般都在20%之内，最大的缆力在沉放过程中为14号锚缆所受到的拉力最大，最大值小于400 kN，小于锚缆的极限拉力500 kN，因而锚缆是安全的。

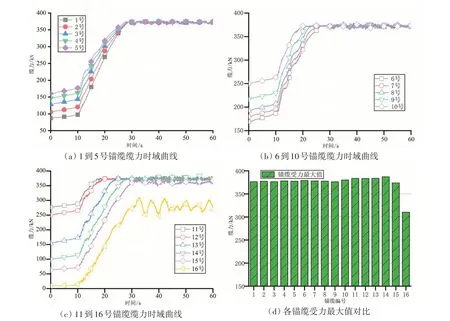
图6 沉放过程钢浮筒锚缆受力分析Fig.6 Dynamic tension analysis for the mooring ropes of the steel buoys in the immersion process

3.1.2 沉放过程驳船及履带吊吊缆受力

图7为沉放过程中吊缆受力的时域曲线，其中图7（a）和图7（b）分别为1到8号驳船吊缆和1号、2号履带吊吊缆缆力的时域曲线图，图7（c）为各锚缆受力最大值对比图。可以看出，所有吊缆和履带吊缆力时域曲线都在0～10 s 之内缓慢单调增加，10～30 s 开始剧烈波动。从幅值的角度来看，各吊缆初始张力均为5 kN，最大幅值出现在吊缆2 号和3 号，较小值为吊缆1 号和8 号。从动张力波动来看，各缆力波动较大原因可能是管道姿态的改变使吊缆出现张紧松弛现象，在沉放过程中偶尔会有个别吊缆松弛，张力降为零。从图7（c）中可以看出，沉放过程中各吊点受力不均，相对差值较大，最大的缆力出现在3 号吊缆，最大值小于400 kN，小于锚缆的极限拉力500 kN，因而吊缆是安全的。为了保证缆力受力均匀性，在受力较大的浮筒处，可适当调整吊缆以减少其受力。

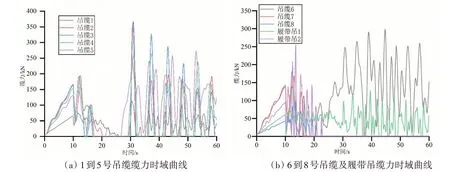
图7 沉放过程驳船吊缆受力分析Fig.7 Dynamic tension analysis of suspension cables of the barges in the immersion process

3.1.3 管道六自由度动力响应

图8 为管道1 的运动响应时域图，弯管由四段钢管焊接成整体，因为管道1 是其中最长的一段钢管，故对管道1 跨中处的六自由度运动响应时域曲线进行讨论。图8（a）～（f）分别为纵荡、横荡、垂荡、纵摇、横摇、首摇的时域曲线。可以发现，所有方向的位移曲线都在0～30 s逐步增加，在30 s处到达最大值，30～60 s 开始按一定的频率波动，振幅收敛于恒定值。从位移幅值来看，总体而言，除垂荡方向显示管道的下沉过程幅值较大外，其他方向位移都很小，证明管道沉放是比较安全和平稳的。

图8 沉放过程中管道1动力响应时域曲线Fig.8 Time-domain curves of dynamic response of Pipeline 1 in the immersion process

3.1.4 管道沿长度方向的受力

沿管道方向各个截面在沉放过程中的受力情况如图9所示。图9（a）～（c）分别为沿管道方向各平截面所受弯矩、扭矩和Mesis应力曲线，可以看出管道弯矩较大，扭矩较小，提示管道受力以弯矩为主。主要原因可能是管道自重和吊缆力较大，而且沉放中管道姿态发生变化，导致管道弯曲变形较大；而由于管道两端、钢浮筒及气囊约束释放了沿管道的扭转自由度，导致管道扭转变形较小。从幅值上看，弯矩、扭矩和Mesis 应力均发生在弯曲角度最大位置处（约310 m 位置），即管道2 和管道3 连接点附近，弯矩最大值接近6 400 kN·m，扭矩最大值接近400 kN·m，Mesis 应力接近46 500 kPa。从曲线变化趋势上看，处于水动力环境弯矩和Mesis应力曲线形状相近，这是由于管道整体受力以弯矩为主，扭矩远小于弯矩。

图9 沿管道方向受力分布情况Fig.9 Stress distribution along the length of the pipeline

3.2 关键参数敏感性分析

参考表2，选取对管道沉放过程的关键参数进行参数敏感性分析。分析时，取各个工况最大受力吊缆的缆力时域曲线和管道1纵荡响应时域曲线进行对比。

3.2.1 气囊放气和管道下放的顺序

气囊放气和下放顺序分为两种：一种是气囊放气和管道下放同时进行；另一种是气囊放气完毕后再进行管道下放，其对最大吊缆受力及管道纵荡响应影响作用见图10。从图10（a）～（b）可以看到，两种不同沉放方式导致了吊缆力和纵荡位移时域曲线出现了较大差别。大体而言，气囊放气完毕后再进行管道下放工况下管道纵荡及吊缆力均较大，该工况下吊缆力达到487 kN 的峰值，纵荡位移接近0.025 m，和同时下放工况相比，幅值增加了大约2 倍。这是因为沉放前放气导致气囊提供的浮力减小，管道剩余重量都由吊缆承担。

图10 不同气囊放气和下放顺序下吊缆力和纵荡位移时域曲线对比Fig.10 Time-domain curves of surge of the pipeline and dynamic tension of suspension cables under different deflated ways and sequences for the airbags

从时域曲线趋势来看，同时下放工况下，在30 s 的曲线大体呈线性增加趋势，全时域曲线波动较小；而先后下放的工况下的时域曲线全时域范围内波动较大，提示该工况下吊缆出现张紧松驰现象，对安全不利。综合来看，从管道受力及动力响应来看，同时下放工况较优。

3.2.2 气囊放气时间

不同气囊放气时间下最大吊缆力和纵荡位移时域曲线对比见图11。通过吊缆力幅值对比可以发现，吊缆力峰值最大的为放气30 s的工况，且放气时间越长缆力最大值越小，纵荡情况也与之相似，放气速率越小，纵荡方向的振幅越小。这是因为气囊体积一定时，放气时间越长放气速率越小，沉放系统状态的变化越平缓，缆力和位移也不会急剧增大，沉放过程也更平稳。因此，可以预知，放气时间越长，沉放过程越安全平稳，所以在设备人员条件许可的情况，可以适当增加放气时间，降低施工风险。

图11 不同气囊放气时间下最大吊缆力和纵荡位移时域曲线对比Fig.11 Time-domain curves of surge of the pipeline and dynamic tension of suspension cables under different deflated times for the airbags

3.2.3 驳船和履带吊吊缆的预张力

对驳船和履带吊的吊缆预张力大小进行敏感性分析，对比工况所采用的预张力取值范围为10～30 kN，如图12 所示。由图12（a）可以看到，一般而言，不同预张力作用下，吊缆动缆力时域曲线波动情况相似，但是幅值并不相同，预张力越大，缆力幅值越小，说明增加吊缆预张力可以有效地抑制沉放系统的缆力动张力，但是对其能量时域分布及频域特性影响不大。通过图12（b）可以看到，同样地，不同预张力作用下，管道纵荡时域曲线波动情况相似，总体而言，预张力越大，纵荡幅值越大。但是总体而言，不同预张力作用下吊缆力和纵荡的差值都不大。因此在工程中，可以适当增加预张力抑制管道动力响应，以保证沉放的安全性，但是预张力越大，也带来缆索容易拉断的隐患，因此应该结合工程实际情况，选择合理的预张力。

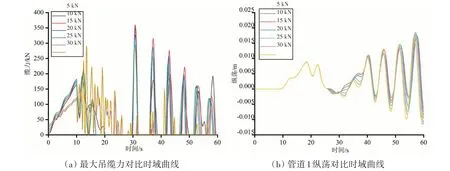
图12 不同吊缆预张力下最大吊缆力和纵荡位移时域曲线对比Fig.12 Time-domain curves of surge of the pipeline and dynamic tension of suspension cables under different pretensions of suspension cables

3.3 数值结果验证

由于作业时间、现场条件、人员安全保障等因素制约，难以实时监测所有浮体在沉放过程中的动力响应和缆索受力情况，实际施工中，选取气囊放气结束后各个吊缆吊点的位移、放气完毕拆除气囊后钢浮筒的浸水深度以及姿态与数值模拟结果进行对比，以检验数值仿真结果，对比情况见图13～14。

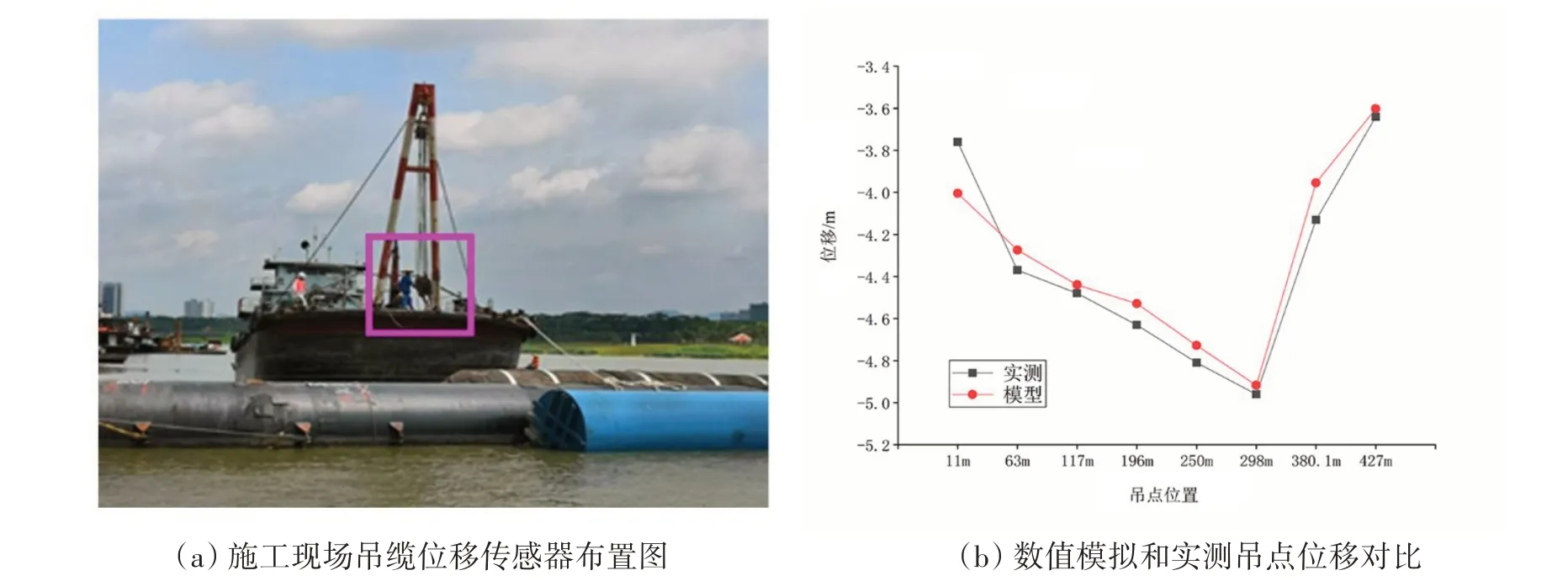
图13 气囊放气结束吊点竖向位移对比Fig.13 Comparison of vertical displacements of suspension points between the field measurement and numerical simulation after airbag deflection

从图13（a）可以看到，圈起来的是设置在吊缆上的位移传感器，可以实时监测吊钩的位移数据。图13（b）是数值计算和实测的气囊放气结束后各个吊点的最终竖向位移的对比分析。从图中容易看出，无论是吊点位移幅值还是曲线形态，数值结果和实测结果都高度吻合，两者曲线均呈现中间低，两头高的形式，均在吊点位置约为300 m处达到峰值。

此外，还可以通过将现场施工各浮体结构的状态和数值模型进行对比来验证模型的准确性。从图14（a）可以看出，沉管系统正处于气囊拆除后的阶段，各钢浮筒均呈现不同程度的下沉，蓝框中区域为钢浮筒位置，可以看到仅剩末端两个钢浮筒还大面积露出水面，其余钢浮筒大部分都完全浸没于水中；从整体钢浮筒的浸没情况、末端钢浮筒的浸水深度及姿态来看，和图14（b）的数值模型基本一致，进一步证明了本次数值计算结果的准确性。

图14 拆除气囊后钢浮筒的浸水深度以及姿态对比图Fig.14 Comparison of attitudes and submerged depths of steel buoys between the field measurement and numerical simulation after airbags deflection

从图14（a）可以看到，沉管系统正处于气囊拆除的阶段，钢浮筒均有不同程度的下沉，框中区域为钢浮筒位置，仅剩末端钢浮筒还大面积露出水面，其余钢浮筒大部分都浸没在水中，而且从末端钢浮筒的浸水深度姿态来看，和图14（b）的数值模型基本一致，进一步证明了本次数值计算结果的准确性。由此可验证拆除气囊到沉放阶段，建模是正确的。

4 结论与施工建议

本文以南宁市邕江过江管道工程水上施工过程为研究背景，对长大弯曲型管道沉放过程中多个浮体之间的复杂耦合作用、整体沉放系统复杂的动力特性进行了研究，主要得到以下结论和施工建议：

（1）当先放气后下放管道时，吊缆缆力大于放气和下放管道同时进行的情况，且沉放过程中的最大值远大于典型工况。数值模拟为纯理论模拟，而管道施工属于危险作业，要尽可能将不安全因素降低，因此，应同时放气和下放，从而施工会更加安全。

（2）气囊放气时间越长，气囊提供的浮力就减小得越慢，缆绳张力和管道应力变化得越慢，缆力和运动响应越小，说明越慢越安全。但是从实际工程考虑，考虑放气速度时，需兼顾安全性和经济性，选择适宜的放气速度。

（3）吊缆初始张力越大，管道纵荡位移越小，因为缆索张力大时对结构动力响应的抑制能力更强。实际施工中，初始张力最好设定为合适的值，用于抵抗流力对管道造成的位置偏移。管道动力响应过大时，可通过调整缆索预张力或者动张力的方式进行控制。

（4）最大应力发生在管道弯曲角度最大位置处，即管道1和管道2连接点处，需引起关注，可以考虑在该位置处增加驳船、钢浮筒及气囊。

（5）沉放过程中，系统出现了一定的吊缆张紧松弛现象，即部分缆索受力大，部分缆索受力小。实践中要注意实时动态测定及调整吊缆缆力，防止出现吊缆张紧松弛现象。