新四维超混沌系统自适应滑模同步
程春蕊,雷腾飞,毛北行
(1.郑州航空工业管理学院 数学学院,河南 郑州 450015;2.齐鲁理工学院 机电工程学院,山东 济南 250200)
混沌同步在安全通信等领域的广泛应用引起了越来越多的研究人员的兴趣,到目前为止,多种控制技术已经成功应用于混沌同步[1-6].滑模控制具有响应快速、设计简单、对参数变化及摄动不灵敏等优点,随着大规模集成电路技术的发展,滑模控制的研究取得了长足的进步,成为控制领域中的一种常用的控制方法.但传统的滑模控制存在一定的抖振问题,而在滑模控制系统的设计中,引入自适应控制在保留了常规滑模控制的鲁棒性的同时削弱了系统的抖振,可以增强滑模控制的品质,在理论和实际应用中都取得了不斐的成绩[7-9].
近年来,随着分数阶微积分的发展,针对非线性系统的分数阶微分建模方法得到了广泛应用.相比整数阶系统,分数阶系统能更精确地描述自然界中的一些物理特性,分数阶滑模控制在滑模控制的基础上,建立分数阶模型,可以提高实际问题的控制性能和精确性,被广泛应用于各个领域[10-13].毛北行等[14]结合分数阶微积分理论,研究了Rössler系统的自适应滑模同步问题,得到了Rössler分数阶混沌系统取得滑模同步的充分条件.
在混沌保密通信中,混沌模型的维数和混沌信号的复杂程度决定着隐藏信息的保密程度,高维超混沌系统具有更好的保密性和通信性能.与混沌现象比较,超混沌至少具有 2 个正的 Lyapunov 指数,这使得超混沌系统具有更强的随机性和不可预测性[15-17].文中运用自适应滑模控制方法,研究整数阶及分数阶的新四维不确定超混沌系统的同步问题.针对整数阶及分数阶的新四维不确定混沌系统,分别设计了自适应滑模同步控制方案,通过构造适当的滑模面和控制器及自适应律得到了新四维超混沌系统取得自适应滑模同步的两个充分条件.数值仿真验证了本文滑模控制方案的有效性.
1 系统描述及主要结果
考虑新四维超混沌系统[17]
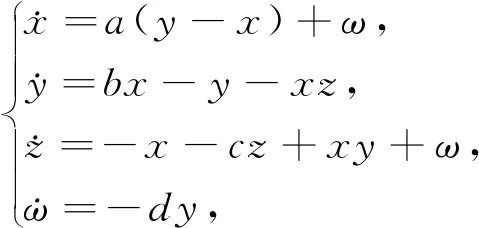
(1)
其中a,b,c,d为常数.当a=24,b=125,c=5,d=10时,采用QR分解方法,用Matlab计算可得:时间t=3000时,系统(1)的4个Lyapunov指数分别为:L1=3.162 199,L2=0.280 214,L3=0.009 005,L4=-33.403 104,如图1所示.
设置初始值为(0.2,0.2,0.2,0.2),则系统的相图如图2所示.系统除具有超混沌行为以外,还存在共存吸引子[18](图3).虚线相图的初始值为[1,1,1,1],实线相图的初始值为[1,1,1,-1].

图1 系统的Lyapunov 指数谱
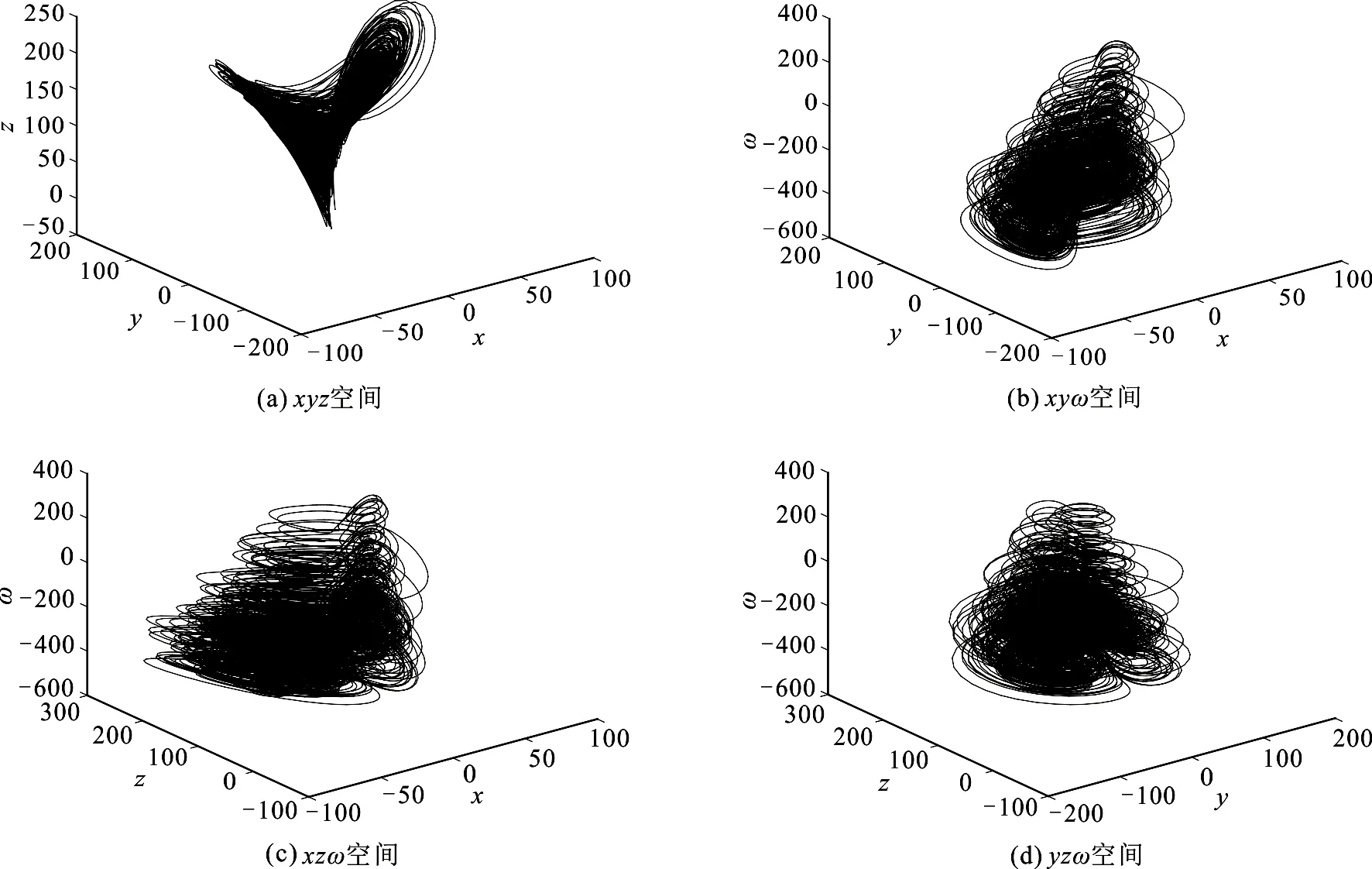
图2 系统轨线在三维空间中的相图

图3 系统的共存吸引子
以(1)为驱动系统,设计响应系统为
(2)
其中Δf(y)表示不确定项,y=[x1,y1,z1,ω1]T为系统的状态向量,d(t)表示外扰,u(t)为控制器.定义误差e1=x1-x,e2=y1-y,e3=z1-z,e4=ω1-ω,得到误差方程
(3)
假设1|Δf(y)|≤m,|d(t)|≤n,其中m,n>0为未知参数.

定理1在假设1下,设计滑模面
控制律
及自适应规则



系统不在滑模面时,构造
求导得

定义1[20]连续函数x(t)的q阶Caputo分数阶导数定义为
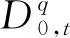
考虑分数阶新超混沌系统
(4)
其中0 (5) 定义误差e1=x1-x,e2=y1-y,e3=z1-z,e4=ω1-ω,得到误差方程 (6) 定理2在假设1下,设计滑模面 控制律 及自适应规则 根据引理2求分数阶导数可得 新四维超混沌系统的误差见图4.从图中可看出,开始时系统误差距离原点较远,在控制器的作用下,误差曲线逐步向坐标原点靠拢,一段时间以后收敛至原点并保持稳定,表明主从混沌系统实现了同步,所提方案具有较好的控制效果. 图4 新四维超混沌系统的误差 基于自适应滑模方法研究了新四维超混沌系统的两个控制方案,获得了新四维超混沌系统的驱动-响应系统达到自适应滑模同步的两个充分条件;从数学角度给出了严格推理和逻辑证明,并用Matlab数值仿真验证了结论的正确性,文中方法对整数阶、分数阶系统均适用.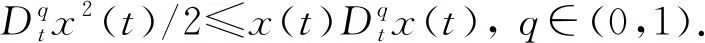


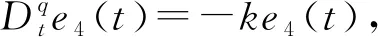

2 数值仿真


3 结束语

