带有恢复率的随机HIV感染模型的灭绝性和平稳分布

曹连英，宋孝吉

(东北林业大学 理学院，黑龙江 哈尔滨 150040)

0 引言

AIDS(获得性免疫缺陷综合症)是由HIV(人类免疫缺陷病毒)引起的一种非常严重的传染性疾病.HIV侵入人体时会攻击人体内带有CD+4分子的T细胞，导致体内CD+4T细胞迅速减少，进而破坏人体免疫系统，导致人体对病毒的抵抗能力迅速下降.伴随人体抵抗能力下降，各种感染随之出现，如肺结核、肺炎、脑炎等，后期常常发生恶性肿瘤，并由于身体长期处于消耗状态而无法抵抗，以至全身器官功能衰竭而死亡.

近年来，国内外许多学者[1-5]根据病毒繁殖机制和人体自身免疫调节理论，建立HIV动力学的数学模型，研究病毒灭绝与持久的阈值条件.

2014年，Sun[6]等建立了具有恢复率的HIV感染模型

(1)

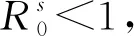
其中x=x(t)表示t时刻未感染的CD+4T细胞浓度，y=y(t)表示t时刻被感染的CD+4T细胞浓度，v=v(t)表示t时刻HIV的浓度;未感染的细胞以恒定速率λ产生，d1表示未感染细胞的正常死亡率，d2表示感染细胞的死亡率，d3表示HIV的死亡率;a表示HIV从感染的CD+4T细胞中产生的速率，p表示在潜伏期内恢复到未感染细胞的速率.Sun[6]等得出：模型(1)的基本再生数R0=ak1/[d3(d2+p)].当R0<1时，系统存在唯一的无病平衡点Q1=(λ/d1,0,0)，且是局部渐进稳定的；当R0>1时，系统存在唯一的地方病平衡点Q2(x*,y*,v*)，且是局部渐进稳定的，其中

现实生活中充满随机性，无时不刻地受到环境白噪声的干扰.环境白噪声会不同程度地影响到出生率、死亡率、竞争系数和系统的其他参数[7]，这对研究随机模型的动力学性质提供了理论基础.Liu等[8]研究具有不同传染性的高阶随机HIV模型，得到模型平稳分布的充分条件；Ji[9]研究B-D型发病率的随机HIV模型，得到病毒灭绝与持久的阈值条件并且证明了系统存在平稳分布的充分条件；Jasmina等[10]基于随机SCIA模型研究HIV模型，得到了病毒灭绝和持久的存在条件.

HIV入侵人体后会对病毒与正常细胞的死亡率产生影响，所以在系统(1)的死亡率中引入随机扰动，即

得到随机系统

(2)

其中δ1,δ2,δ3表示噪声强度，Bi(i=1,2,3)为独立的布朗运动.

文中首先研究系统(2)全局正解的存在唯一性和疾病灭绝的阈值条件，然后给出系统(2)存在平稳分布的阈值条件，并证明系统的平稳分布；最后，通过数值模拟检验理论分析的有效性.

1 全局正解的存在唯一性

证明应用文献[9]的方法易证系统(2)的系数满足局部Lipschitz条件，对

系统(2)在t∈[0,τe]时刻内存在唯一的局部解X(t)=(x(t),y(t),v(t))，其中τe为解的爆破时间[11].为了证明解的全局性只需证明τe=∞几乎处处成立即可.

设m0≥1足够大，使得初值X0的每一个分量均位于区间[1/m0,m0]中，对整数m≥m0，定义停时

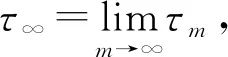
假设τ∞≠∞，则存在常数T>0和ε∈(0,1)使得P{τ∞≤T}>ε,即存在整数m1≥m0，对∀m≥m1，都有P{τm≤T}≥ε.

其中K是一个正常数.于是

对(4)式两边从0到τm∧T=min(τm,T)积分，并取期望可得

设Ωm={τm≤T}，m≥m1,则P(Ωm)≥ε.对∀ω∈Ωm，由停时的定义，x(τm,ω),y(τm,ω),v(τm,ω)中至少有一个等于m或1/m，因此

由(5)式可得

其中IΩm(ω)为Ωm(ω)的示性函数.当m→∞时，有∞>V(x(0),y(0),v(0))+KT=∞，矛盾.因此必有τ∞=∞几乎处处成立 】.

2 疾病的灭绝性

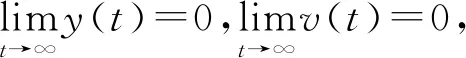
其中

显然

令

显然M1(t),M2(t)是连续局部鞅.由鞅的强大数定律，几乎处处有

(9)

对(6)式两边从0→t积分，有

对(10)式两边同除以t并取极限可得

3 平稳分布

引理1[12]假设X(t)是En(n维欧几里得空间)中的一个自治Markov过程，定义为

其扩散矩阵

Markov过程X(t)有唯一的平稳遍历分布μ(·).如果存在一个有正则边界Γ的有界区域U∈En且满足下列性质：

(A1)存在一个常数K，使得

(A2)存在一个非负的C2函数V,使得对EnU有LV<0，则

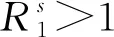
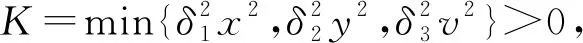
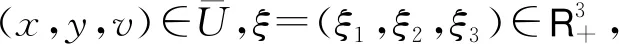
其中0<θ<1是一个常数，满足

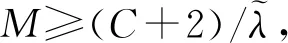
类似地，有

根据文献[13]中的不等式

有

其中

将(14)～(17)式代入(13)式可得

构造紧子集

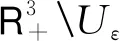
这里

情况1：(x,y,v)∈U1.此时

情况2:(x,y,v)∈U2.此时

因为

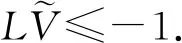
情况3:(x,y,v)∈U3.此时

情况4:(x,y,v)∈U4.此时

情况5:(x,y,v)∈U5.此时

情况6:(x,y,v)∈U6.此时

4 数值模拟

应用文献[14]Milstein高阶方法，得到系统(2)的迭代方程为

其中ε1k,ε2k和ε3k(k=1,2,…,n)是独立高斯随机变量N(0,1),δi(i=1,2,3)是白噪声强度.

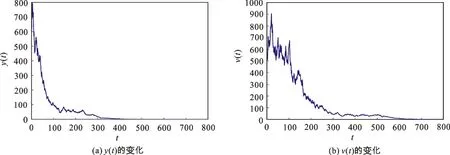
图1 y(t),v(t)依概率1灭绝

图2 x的随机模拟频率柱状图

5 结论