强Gorenstein FP-gr-内射模

张翠萍，杨银银

(西北师范大学 数学与统计学院,甘肃 兰州 730070)

0 引言

1969年，Auslander等[1]对双边Noetherian环上有限生成模引入了G-维数的定义，此后，Enochs等[2-3]对一般环引入了Gorenstein投射(内射， 平坦)模的概念．2007年，Bennis等[4]研究了强Gorenstein投射(内射, 平坦)模;丁南庆等[5-6]研究了Gorenstein FP-内射模、Gorenstein平坦模的性质及其联系;高增辉等[7]给出了Gorenstein FP-内射模的另一种定义，并研究了其性质以及强Gorenstein FP-内射模的性质．

近年来，分次环的同调理论在代数几何中得到了广泛应用.1998年，Asensio等[8-9]引入了Gorenstein gr-投射(内射, 平坦)模，讨论了这些模类的性质以及与未分次下相应模类之间的关系，进而文献[10-11]研究了分次模范畴中模的Gorenstein投射(平坦)覆盖及Gorenstein内射包络．毛立新[12]研究了强Gorenstein gr-投射(内射, 平坦)模，得到了许多与未分次情况下类似的结论．2000年，Asensio等[13]引入了FP-gr-内射模并刻画了其性质．2011年，Yang等[14]进一步研究了FP-gr-内射模以及分次模的FP-gr-内射包络和FP-gr-内射覆盖．2018年,高增辉等[15]把Gorenstein FP-内射模的相关性质推广到了分次环上．

受以上工作的启发，文中研究强Gorenstein FP-gr-内射模的性质，讨论强Gorenstein FP-gr-内射模与强Gorenstein gr-平坦模之间的关系以及这类模在分次与未分次之间的联系．

1 预备知识

除非特别说明，文中环均指有单位元1的结合环，模均指酉模．

设G是乘法群，e为其单位元．称环R为分次环，如果它有一个加法子群的直和分解R=⊕σ∈GRσ,使得对任意的σ,τ∈G，有RσRτ=Rστ．易得Re是R的一个子环，1∈Re且对任意σ∈G，Rσ是Re-双模．称左R-模M是分次左R-模，如果M有一个加法子群的直和分解M=⊕σ∈GMσ，使得对任意σ,τ∈G，有RσMτ⊆Mστ．显然对任意σ∈G，Mσ是左Re-模．

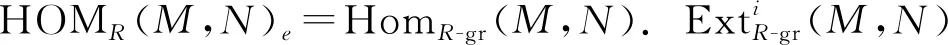
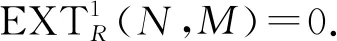
定义1[12]称分次左R-模M是强Gorenstein gr-平坦模，如果在R-gr中存在一个gr-平坦左R-模的正合列

使得M≅Kerα，且对任意的gr-内射右R-模I，有I⊗R-grF正合．

定义2[15]称分次左R-模M是Gorenstein FP-gr-内射模，如果存在一个FP-gr-内射左R-模的正合列

使得M≅Ker(E0→E1)，且对任意满足pd(P)<∞的有限表示分次左R-模P，有HomR-gr(P,E)正合．

定义3[17]称左R-模M是强Gorenstein FP-内射模，如果存在一个FP-内射左R-模的正合列

使得M≅Kerα，且对任意满足pd(P)<∞的有限表示左R-模P，有HomR(P,E)正合．

2 强Gorenstein FP-gr-内射模

定义4设R是分次环．称分次左R-模M是强Gorenstein FP-gr-内射模，如果在R-gr中存在一个FP-gr-内射左R-模的正合列

使得M≅Kerα，且对任意投射维数有限的有限表示分次左R-模P，有HomR-gr(P,E)正合．

注1由定义4可知，强Gorenstein FP-gr-内射模类关于直积封闭；强Gorenstein FP-gr-内射左R-模是Gorenstein FP-gr-内射的．

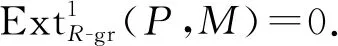
证明必要性.显然．

充分性.设在R-gr中存在正合列0→M→E→M→0，其中E是FP-gr-内射左R-模，则有正合列

命题2设R是分次环，则每个FP-gr-内射左R-模是强Gorenstein FP-gr-内射的．

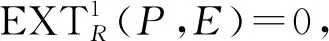
文献[12]定理2.4证明了每个Gorenstein gr-内射左R-模是某个强Gorenstein gr-内射左R-模的直和项．

定理1设R是分次环，则每个Gorenstein FP-gr-内射左R-模是某个强Gorenstein FP-gr-内射左R-模的直和项．

证明设M是Gorenstein FP-gr-内射左R-模，则在R-gr中存在FP-gr-内射左R-模的正合列

使得M≅Kerf0，且对任意满足pd(P)<∞的有限表示分次左R-模P，有HomR-gr(P,E)正合．

设N=∏Ei，则N是FP-gr-内射左R-模，定义f:N→N．令f=∏f，易得f∈HomR-gr(N,N)，在R-gr中得到复形

又因为Imf=∏Imfi=∏Kerfi=Kerf，所以复形C是正合的．对任意的有限表示分次左R-模P且pd(P)<∞，有

HomR-gr(P,C)≅(HomR-gr(P,E))N.

由HomR-gr(P,E)正合可知HomR-gr(P,C)正合,故M是强Gorenstein FP-gr-内射左R-模． 】

文献[15]定理2.1证明了在左gr-凝聚环上，分次左R-模M是Gorenstein FP-gr-内射模当且仅当存在定义2中的正合列．类似可得下列结论．

定理2设R是左gr-凝聚环，M∈R-gr，则M是强Gorenstein FP-gr-内射左R-模当且仅当存在一个FP-gr-内射左R-模的正合列

使得M≅Kerα．

证明必要性.显然．

充分性.设存在一个FP-gr-内射左R-模的正合列

使得M≅Kerα．只需证明对任意满足pd(P)<∞的有限表示分次左R-模P，有HomR-gr(P,E)正合．不妨设pd(P)=m<∞，对m进行归纳．

若m=0， 则结论显然成立．

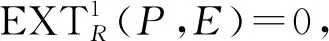
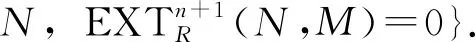
定义分次左R-模M的Gorenstein FP-gr-内射维数为：G-FP-gr-idR(M)=inf{n|存在正合列0→M→E0→E1→…→En→0，其中Ei是Gorenstein FP-gr-内射左R-模}．如果这样的n不存在，则记G-FP-gr-idR(M)=∞．

命题3设R是左gr-凝聚环，则以下各结论等价：

(1)每个强Gorenstein FP-gr-内射左R-模是FP-gr-内射的；

(2)每个Gorenstein FP-gr-内射左R-模是FP-gr-内射的；

(3)对每个分次左R-模M，G-FP-gr-idR(M)=FP-gr-idR(M)．

证明(1)⇒(2).设M是Gorenstein FP-gr-内射左R-模，则由定理1可知，存在强Gorenstein FP-gr-内射左R-模N，使得M是N的直和项．由已知N是FP-gr-内射左R-模，故M是FP-gr-内射左R-模．

(2)⇒(1).设M是强Gorenstein FP-gr-内射左R-模，由注1知，M是Gorenstein FP-gr-内射左R-模，故M是FP-gr-内射左R-模．

(2)⇒(3).设M是分次左R-模，由文献[14]引理3.7知,G-FP-gr-idR(M)≤FP-gr-idR(M)．下面证明FP-gr-idR(M)≤G-FP-gr-idR(M)．假设G-FP-gr-idR(M)=m<∞，则存在正合列0→M→E0→…→Ei→…→Em→0,其中Ei是Gorenstein FP-gr-内射左R-模，0≤i≤m．由(2)知，Ei是FP-gr-内射的．由文献[14]引理3.7知，FP-gr-idR(M)≤m，故G-FP-gr-idR(M)=FP-gr-idR(M)．

(3)⇒(2)显然． 】

文献[12]定理3.10讨论了强Gorenstein gr-平坦模和强Gorenstein gr-内射模之间的关系，以下我们讨论强Gorenstein gr-平坦模和强Gorenstein FP-gr-内射模之间的关系．

命题4设R是左gr-凝聚环，M∈R-gr．如果M是强Gorenstein gr-平坦的，那么M+是强Gorenstein FP gr-内射右R-模．

证明设M是强Gorenstein gr-平坦的，则在R-gr中存在gr-平坦左R-模的正合列

使得M≅Kerα．由文献[13]定理3.5知，存在FP-gr-内射右R-模的正合列

使得M+≅Ker(α+)．再由定理2知，M+是强Gorenstein FP-gr-内射右R-模． 】

称环R是gr-n-FC环，如果R是左右gr-凝聚环，且RR,RR分别有有限FP-gr-内射维数[9]．

命题5设R是gr-n-FC环，M∈R-gr．如果M是强Gorenstein FP-gr-内射左R-模，那么M+是强Gorenstein gr-平坦右R-模．

证明设M是强Gorenstein FP-gr-内射左R-模，则在R-gr中存在FP-gr-内射左R-模的正合列

使得M≅Kerα．由文献[13]定理3.7知，存在gr-R中的正合列

使得M+≅Ker(α+)，E+是gr-平坦的．由文献[12]定理3.10知，M+是强Gorenstein gr-平坦右R-模． 】

设U:R-gr→R-Mod是遗忘函子，它把R-gr中的分次左R-模M映成不考虑分次结构的左R-模M．令F:R-Mod→R-gr是U的右伴随函子，它把R-Mod中的左R-模M映成分次左R-模F(M)，其中F(M)=⊕σ∈GσM,σM=M,σM中的元记为：σM={σx|x∈M},R-模结构定义为：r*τx=τσ(rx).如果f:M→N是R-线性的，则F(f)：F(M)→F(N)是一个分次态射，其中F(f)(σx)=σf(x)．特别地，当G是有限群时，由文献[19]定理2.5.1知，(F,U)是一个伴随对．

下面讨论强Gorenstein FP-内射模与强Gorenstein FP-gr-内射模之间的关系．

命题6设R是分次环，M∈R-gr．如果M是强Gorenstein FP-内射模，那么F(M)是强Gorenstein FP-gr-内射的．

证明设M是强Gorenstein FP-内射模，则存在FP-内射左R-模的正合列

使得M≅Kerα，且对任意投射维数有限的有限表示左R-模P，有HomR(P,E)正合．因为F是正合函子，所以有R-gr中的正合列

使得F(M)≅Ker(F(α))．由文献[14]引理2.3知，F(E)是FP-gr-内射的．

设Q是任意投射维数有限的有限表示分次左R-模，下证HomR-gr(Q,F(E))正合．因为(U,F)是伴随对，所以有同构式

HomR(U(Q),-)≅HomR-gr(Q,F(-)),

从而得到交换图

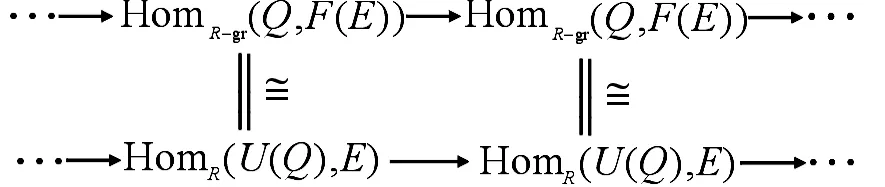
由于U(Q)是投射维数有限的有限表示左R-模，上图中的下行正合，因此上行是正合的，即有HomR-gr(Q,F(E))正合．从而F(M)是强Gorenstein FP-gr-内射的． 】

命题7设R是分次环，G是有限群，M∈R-gr．如果M是强Gorenstein FP-gr-内射模，那么U(M)是强Gorenstein FP-内射的．

证明设M是强Gorenstein FP-gr-内射模，则存在FP-gr-内射左R-模的正合列

使得M≅Kerα，且对任意投射维数有限的有限表示分次左R-模P，有HomR-gr(P,E)正合．因为U是正合函子，所以存在左R-模正合列

使得U(M)≅Ker(U(α))．由文献[14]推论2.4知，U(E)是FP-内射的．

设Q是任意投射维数有限的有限表示左R-模，下证HomR(Q,U(E)正合．因为G是有限群，所以有同构式

HomR-gr(F(Q),-)≅HomR(Q,U(-)),

从而得到交换图

因为G是有限群，所以F(Q)是投射维数有限的有限表示分次左R-模，上图中下行正合，从而有上行正合，即HomR(Q,U(E))正合．故U(M)是强Gorenstein FP-内射的． 】