形式三角矩阵环上的Gorenstein 平坦模
杨晓燕,李 清
(西北师范大学 数学与统计学院,甘肃 兰州 730070)
0 引言

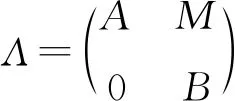

1 预备知识

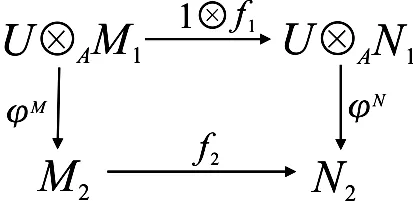
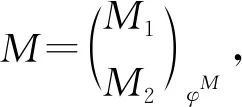
类似地,右T-模范畴中的对象可以用三元组W=(W1,W2)φW来表示,其中W1是右A-模,W2是右B-模,φW:W2⊗BU→W1是A-模同态.任意两个右T-模(W1,W2)φW和(X1,X2)φX之间的态射是二元组(g1,g2),其中g1:W1→X1是A-模同态,g2:W2→X2是B-模同态,并且满足交换图

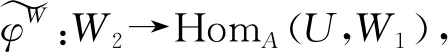
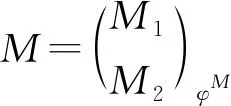


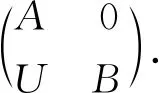
2 Gorenstein 平坦模
定义1一个完全平坦分解是平坦R-模的正合列
P: …→P1→P0→P0→P1→…,
使得对任意的内射右R-模I,有I⊗RP正合.
称左R-模M是Gorenstein平坦模,若存在一个完全平坦分解P,使得M≅Ker(P0→P1).
定义2称U是相对于平坦分解的相容左B右A-双模,若以下两个条件成立:
(C1)若P是完全左B-模平坦分解,则HomA(U,E)⊗P正合,其中E为内射右A-模.
(C2)若F是平坦左A-模的正合列,则U⊗AF是正合的.
例1设U是左B右A-双模,fd(UA)<∞.若fd(BU)<∞,则U是相对于平坦分解的相容双模.
证明设Q是平坦左A-模的正合列.考虑右A-模U的平坦分解
0→Fn→Fn-1→…→F1→F0→U→0,
其中F1是平坦的,i∈Z,则F1⊗AQ是正合的.因为Fi是平坦的,所以得到复形的正合列
于是U⊗Q正合,故U满足条件(C2).若fd(BU)=m<∞,E是内射右A-模,则由文献[10]知,对任意右B-模Y,有
所以id(HomA(U,E))≤m<∞.设P是完全左B-模平坦分解,则由文献[5]知,HomA(U,E)⊗P正合.因此U满足条件(C1),所以U是相对于平坦分解的相容双模. 】
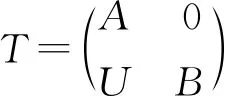
(1)M是Gorenstein平坦左T-模;
(2)M1是Gorenstein平坦左A-模,Coker(φM)是Gorenstein平坦左B-模且φM是单同态.
证明(1)⇒(2).因为M是Gorenstein平坦左T-模,所以存在完全左T-模平坦分解

其中M1=Ker(∂0).
设λ1:M1→F0和λ2:M2→P0.考虑交换图

因为U是相对于平坦分解的相容双模,所以U⊗AF正合.于是1U⊗λ1是单同态.由文献[7]知,φ0是单同态.于是由交换图知,φM是单同态.对∀i∈Z,有如下交换图:

因为第一列和第二列正合,所以得到平坦左B-模的正合列
由文献[10]知,Coker(φM)≅Ker(α0).设G是内射右B-模,则有左B-模的正合列
0→U⊗AFi→Pi→Coker(φi)→0,
从而得到正合列
所以
因为(0,G)是内射右T-模,所以G⊗S≅(0,G)⊗TH正合,于是S是完全左B-模平坦分解,因此Coker(φM)是Gorenstein平坦左B-模.
设E是内射右A-模,则存在右T-模的正合列
于是有复形正合列
因为(E,HomA(U,E))是内射右T-模,所以复形(E,HomA(U,E))⊗TH是正合的.又因为U是相对于平坦分解的相容双模,所以HomA(U,E)⊗S正合.于是
正合.故由文献[10]知,(E,0)⊗TH≅E⊗AF正合.因此F是完全左A-模平坦分解,所以M1是Gorenstein平坦左A-模.
(2)⇒(1).因为φM:U⊗AM1→M2是单同态,所以存在左T-模的正合列
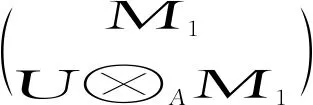
使得M1=Ker(∂0),由条件(C2)知,U⊗AF正合.于是存在平坦左T-模的正合列

0→(E1,0)→(E1,E2)→(0,E2)→0.

因为
所以
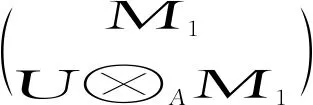

使得Coker(φM)=Ker(d0).于是存在平坦左T-模的正合列

因为(E,HomA(U,E))是内射右T-模,所以
(E,HomA(U,E))⊗TΩ≅HomA(U,E)⊗BP.


证明由例1知,U是相对于平坦分解的相容双模,所以结论成立. 】

证明因为RRR是相对于平坦分解的相容双模,所以结论成立. 】

