Frobenius双模和Gorenstein AC-平坦模
王占平,白 洁
(西北师范大学 数学与统计学院,甘肃 兰州 730070)
0 引言
作为平坦模在Gorenstein同调代数中的对应,1993年,Overtoun等[1]引入了Gorenstein平坦模,并研究了其性质.2009年,Ding等[2]定义了强Gorenstein平坦模.2010年, Gillespie[3]将强Gorenstein平坦模称为Ding投射模,并进一步研究了其性质.为了研究一般环上的稳定模范畴,2014年,Bravo等[4]引入了FP∞型模、绝对clean模和Gorenstein AC-投射模.2019年,Iacob[5]引入了Gorenstein AC-平坦模,并研究了其性质.
1954年,Kasch[6]以Frobenius代数为基础,引入了Frobenius扩张.1960年,Nakayam等[7]和Morita[8]对Frobenius扩张做了进一步研究.1999年,Kadison[9]深入研究了Frobenius扩张,并且引入了Frobenius双模的概念.近来,Ren[10-12]研究了Frobenius扩张上的Gorenstein投射(内射, 平坦)模及其维数,Hu等[13]研究了Frobenius函子和Gorenstein平坦模之间的关系.
受以上结论的启发,文中研究Frobenius双模和Gorenstein AC-平坦模之间的关系.
文中环R和S均是有单位元的结合环,模均指酉模.所有的左R-模(或者左S-模)表示为R-模(或者S-模),所有的右R-模(或者右S-模)表示为ROP-模(或者SOP-模).对任意环R,RM表示所有R-模的范畴且MR表示所有ROP模的范畴,SMR表示M是一个(S,R)-双模.F(R)表示所有平坦R-模构成的类.
1 Frobenius 双模和 Gorenstein AC-平坦模
定义1[9]称(S,R)-双模M是Frobenius双模,如果满足以下条件:
(1)模SM和MR都是有限生成投射模;
(2)存在(R,S)-双模的同构:
*M:=RHomS(M,S)S≅RHomROP(M,R)S=:M*.
称S⊆R是Frobenius扩张[7],如果SR是有限生成投射S-模,且RRS≃HomS(SR,SS).此定义等价于RS是有限生成投射SOP-模,且SRR≃HomSOP(RS,SS).在这种情况下,SRR和RRS均是Frobenius双模.
定义2[4]称R-模X是FP∞型模,如果存在X的投射分解
…→P2→P1→P0→X→…,
其中对任意的i≥0,Pi是有限生成投射模.当环R是左Noetherian环时,FP∞型R-模是有限生成R-模;当R是左凝聚环时,FP∞型R-模是有限表示R-模.
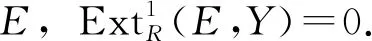
以下FJ∞(R)表示绝对cleanR-模类.
注1[4]环R是左凝聚环当且仅当每个绝对cleanR-模就是绝对纯R-模.
定义4[5]称R-模W是Gorenstein AC-平坦模,如果存在平坦R-模的正合序列
F: …→F2→F1→F0→F0→F1→…,
使得W≅Ker(F0→F1),且对任意ROP-模E∈FJ∞(ROP),有E⊗RF正合.
记GFAC(R)为所有Gorenstein AC-平坦R-模构成的类.显然,Gorenstein AC-平坦模是Gorenstein平坦模.
引理1[9,14]设R和S是环,SMR是Frobenius双模,令N:=*M, 则以下结论成立:
(1)RNS是Frobenius双模;
(2)M⊗R-≅HomR(N,-):RM→SM,
N⊗S-≅HomS(M,-):SM→RM;
(3)HomROP(M,-)≅-⊗RN:MR→MS,
HomSOP(N,-)≅-⊗SM:MS→MR;
(4)若X是投射(内射, 平坦)R-模,则M⊗RX是投射(内射, 平坦)S-模;
(5)若Y是投射(内射, 平坦)S-模,则HomS(M,Y)是投射(内射, 平坦)R-模;
(6)对任意的i≥0及任意的S-模X和R-模Y,有
(7)对任意的i≥0及任意的ROP-模X和R-模Y,有
文献[16]给出了Frobenius函子的概念.设A和B均是Abel范畴,F:A→B,G:B→A是函子.称函子对(F,G)是Frobenius对,如果G既是F的左伴随又是它的右伴随.称函子F:A→B是Frobenius函子,如果对于函子G:B→A, (F,G)是Frobenius对.
根据文献[16]可知,函子F:RM→SM是Frobenius函子当且仅当存在Frobenius双模SMR使得F≅M⊗R-.
引理2[13]设SMR是Frobenius双模,N:=*M且F:M⊗R-:RM→SM是Frobenius函子, 则以下结论等价:
(1)F是忠实函子;
(2)RN是生成子;
(3)MR是生成子;
(4)MR是忠实的;
(5)对任意的R-模X,映射φX:X→HomS(M,M⊗RX)(φX(x)(m)=m⊗Rx)是单同态,其中x∈X且m∈M;
(6)对任意的ROP-模Y,映射ψY:HomROP(M,Y)⊗SM→Y(ψY(f⊗Sm)=f(m))是满同态,其中f∈HomROP(M,Y)且m∈M;
(7)对任意的R-模P∈P(R),映射ΦP:N⊗SHomR(N,P)→P(ΦP(n⊗Sf)=f(n))是满同态,其中f∈HomR(N,P)且n∈N;
(8)对任意的ROP-模E∈J(ROP),映射θE:E→HomSOP(N,E⊗RN)(θE(x)(n)=x⊗Rn)是单同态,其中x∈E且n∈N.
引理3设SMR是Frobenius双模.
(1)若X是FP∞型R-模,则M⊗RX是FP∞型S-模;
(2)若Y是FP∞型S-模,则HomS(M,Y)是FP∞型R-模.
证明(1)因为X是FP∞型R-模,所以存在X的投射分解
P: …→P2→P1→P0→X→0,
其中对任意i≥0,Pi是有限生成投射R-模.因为SMR是Frobenius双模,所以用M⊗R-作用于上述序列,可得S-模的正合列
因为M⊗RPi是有限生成投射S-模,所以M⊗RP是M⊗RX的有限生成投射分解.故M⊗RX是FP∞型S-模.
(2)因为Y是FP∞型S-模,所以存在Y的投射分解

引理4设SMR是Frobenius双模.
(1)若X是绝对cleanR-模,则M⊗RX是绝对cleanS-模;
(2)若Y是绝对cleanS-模,则HomS(M,Y)是绝对cleanR-模.

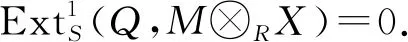
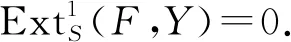
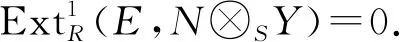
定理1设SMR是Frobenius双模.
(1)若X是Gorenstein AC-平坦R-模,则M⊗RX是Gorenstein AC-平坦S-模;
(2)若Y是Gorenstein AC-平坦S-模,则HomS(M,Y)是Gorenstein AC-平坦R-模.
证明(1)因为X是Gorenstein AC-平坦R-模,所以存在平坦R-模的正合列
F: …→F1→F0→F-1→F-2→…,
使得X≅Ker(F-1→F-2),且对任意ROP-模E∈FJ∞(ROP),有E⊗RF正合.因为Fi是平坦R-模,所以M⊗RFi是平坦S-模.因此
是平坦S-模的正合序列,且M⊗RX≅Ker(M⊗RF-1→M⊗RF-2).
设B是绝对cleanSOP-模,则B⊗SM是绝对cleanROP-模,因此(B⊗SM)⊗RF正合.由同构(B⊗SM)⊗RF≅B⊗S(M⊗RF)知,B⊗S(M⊗RF)正合.因此M⊗RX是Gorenstein AC-平坦S-模.
(2)因为Y是Gorenstein AC-平坦S-模,所以存在平坦S-模的正合列

是平坦R-模的正合序列,且
设E是绝对cleanROP-模,则HomROP(M,E)是绝对cleanSOP-模,故HomROP(M,E)⊗SF′正合.令N: =*M.因为SMR是Frobenius双模,所以RNS是Frobenius双模,且HomROP(M,E)≅E⊗RN.由同构
知,E⊗RHomS(M,F′)正合. 所以HomS(M,Y)是Gorenstein AC-平坦R-模. 】
引理5设X是R-模,则以下结论等价:
(1)X是Gorenstein AC-平坦R-模;

0→X→F0→F1→F2→…;
(3)存在短正合列0→X→F→G→0,其中F是平坦模,G是Gorenstein AC-平坦模.
引理6[5,15]GFAC(R)关于扩张和直和项封闭.
定理2设SMR是Frobenius双模,MR是生成子.若任意绝对cleanROP-模B是HomROP(M,B)⊗SM的直和项,则R-模X是Gorenstein AC-平坦模当且仅当M⊗RX是Gorenstein AC-平坦S-模.
证明必要性.由定理1可得.
充分性.设X是R-模,使得M⊗RX是Gorenstein AC-平坦S-模.以下证明X是Gorenstein AC-平坦R-模.
设B是绝对cleanROP-模,则HomROP(M,B)是绝对cleanSOP-模.因为M⊗RX是Gorenstein AC-平坦S-模,所以对任意的i≥0,有
由同构
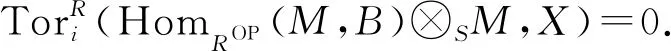
由定理1可知,HomS(M,M⊗RX)是一个Gorenstein AC-平坦R-模.因此存在短正合序列
0→HomS(M,M⊗RX)→F0→L1→0,
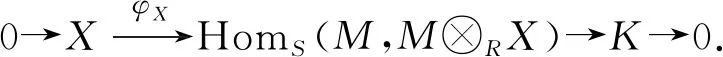
考虑下列推出图
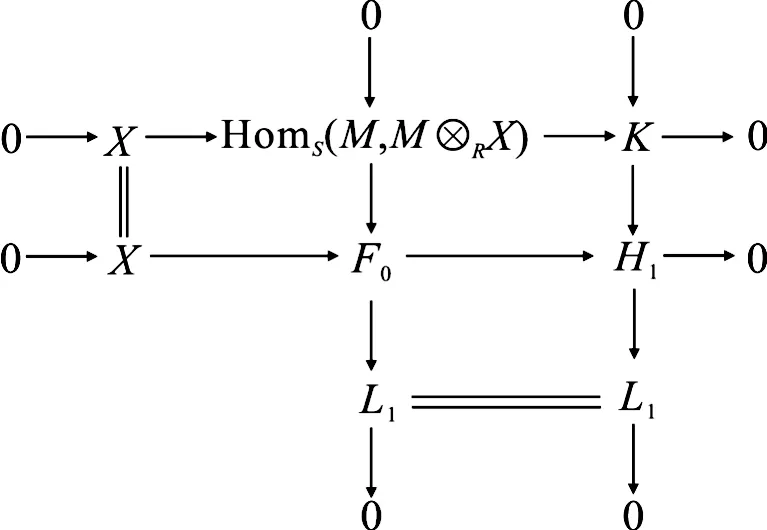
用M⊗R—作用后,得到
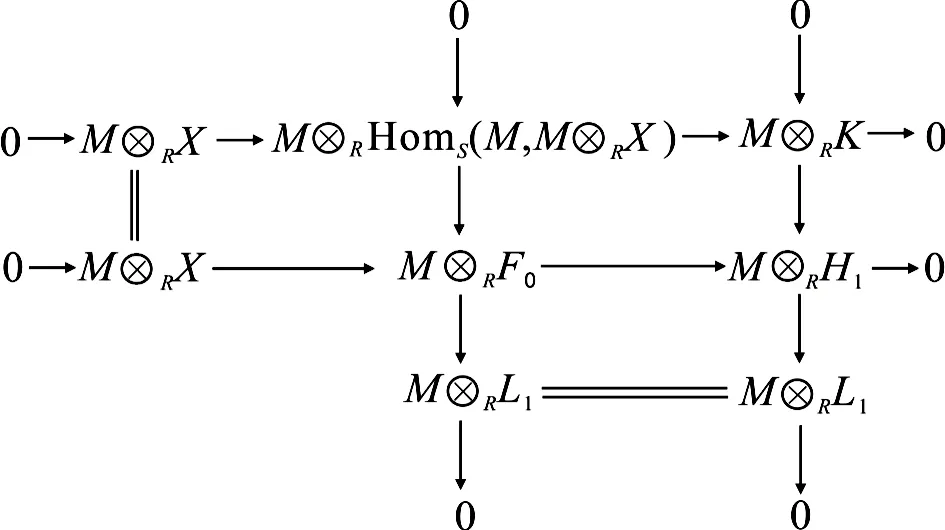
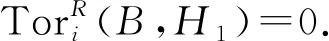
0→X→F0→F1→F2→…,
使得对任意的ROP-模Q∈FJ∞(ROP),有Q⊗R-正合.故X是Gorenstein AC-平坦R-模. 】

