初中数学中的化归思想案例分析

陈春宇（吉林师范大学，吉林 长春 130000）

一、引言

素质教育正在逐步取代应试教育，如何将学生的综合能力提升，成为当前教师需要解决的重点问题.我们知道数学这门学科是一个具有较强逻辑性的科学，数学中的知识大多都具有连贯性；教材中的数学知识编排也是由浅至深，由易到难.化归思想贯串整个数学学习过程中，是一个极其重要的解题思想，那么这就要求教师能够在教学过程中渗透化归思想，实现学生在学习了某些新的偏难的知识后，能够自觉选择并熟练运用化归思想将问题进行简单化处理.这样来看，基于数学核心素养下的化归思想，既有助于提升学生的逻辑推理能力和数学运算能力，又能够有效地锻炼学生的数学思维，让学生能够拥有良好的数学素养，增强课堂教学质量，提升学生的学习效率，这无疑是一种提升学生综合能力的有效途径.下面笔者将结合初中数学教学内容中所涉及的能够充分体现化归思想的案例来进行具体分析.

二、在有理数的运算中体现的化归思想

在初中数学人教版教材中，七年级上册第一章节的内容就是有理数，初中阶段最先接触的数的运算也是有理数的运算.有理数的运算包括有理数的加法、减法、乘法、除法以及乘方，在这些有理数的运算过程中隐藏着许多化归思想.

在进行有理数的减法运算时，我们应先将减法转化为加法，再根据有理数的加法法则来进行计算.例如，当计算8-(-2)时，我们要将括号之前的减号变为加号，再将括号中的减数变成它的相反数，经过转化后得到8＋2 ＝10.因为减去一个负数这样的逆向思维学生会很难理解，所以将减法运算变为加法运算就是一个化繁为简的过程，学生更易接受.学生后面还要学习有理数的加减法混合运算，这样的转化方法，使混合运算统一为加法运算，再结合适当的加法运算律来计算，就会使原本复杂的混合运算变得容易计算.

有理数的除法运算与有理数的减法运算有着类似的转化思路，就是先将除法转换为乘法，再根据有理数的乘法法则来进行计算.例如，当计算时，我们要将除号先变为乘号，再将除数变为它的倒数，经过转化可以得到.学生先学习了乘法，自然会对乘法有着固化思维，除法是乘法的逆运算.因此，将除法转化为乘法更易让学生理解和计算.

先学了加法，就把减法转化为已熟悉的加法来计算；先学了乘法，就把除法转化为已熟悉的乘法来计算.减法法则和除法法则是有理数运算中最典型的化归思想，是我们学习数学必须掌握的最基本的两种运算法则.

三、在代数式的运算中体现的化归思想

在初中阶段的代数式的运算过程中，课标要求学生熟练掌握去括号法则、合并同类项法则以及整体代入法则，以实现整式的化简求值.

将b＝2 代入，得原式＝8b＝8×2＝16.

该题要求“化简”式子，顾名思义，就是将5（a＋b-c）-3（a-b-c）-2（a-c）化繁为简，即要求运用化归思想来解决该问题.这类题的化归思想为：当遇到几个整式相加减的式子，如果有括号的就先去掉括号，然后进行合并同类项的过程，将同类项的系数相加减，字母连同它的指数都不变，最后将原来较为复杂的整式转化为简单的有理数相加减的形式来得到最简代数式.

例2代数式x2＋4x-3 的值为3，则2x2＋8x-7 的值为多少？

解：由题意得x2＋4x-3＝3，则x2＋4x＝6.

又因为2x2＋8x-7＝2（x2＋4x）-7，

故原式＝2×6-7＝5.

本题是求代数式的值，但根据已知条件求出x的值再求代数式的值会很麻烦，所以本题中可以先根据已知条件求出x2＋4x的值，将x2＋4x看成一个整体，再找出2x2＋8x-7与x2＋4x的关系，目的是从2x2＋8x-7 中变出这个整体，即变为2(x2＋4x)-7，最后将x2＋4x整体代入后求值.整体代入法则是求代数式的值的一般方法，即将所求的代数式变形为已知的代数式表示的形式，然后代入数值进行计算的解题方法.运用这种化部分为整体的化归思想来解决此类问题，可以使得解题步骤更为简单.

四、在解方程与解方程组的运算中体现的化归思想

前面所学过的有理数和代数式的运算均为接下来的解方程和解方程组奠定了化归思想基础.解方程和解方程组的基本思路就是将未知数的次数由高次转化为低次、将无理方程转化为有理方程、将分式方程转化为整式方程以及将多元方程转化为一元方程，在这些转化过程中无一不是运用了化归思想，即不断通过变形和转化将原方程变成与它等价的最简单的方程的过程.化归思想是学生会求解方程和方程组的核心思想.

例3求一元二次方程x2-5x＝0 的根.

解：等式左边提出公因式x，可得x（x-5）＝0，

解得x1＝0，x2＝5.

降次法是指将高次方程转化为低次方程，本题求一元二次方程，就是将一元二次方程降次为一元一次方程来求解.

例4解无理方程.

解：将等式两边分别平方，得x＋2＝16，解得，x＝14.

经检验，x＝14 是原方程的根，所以原方程的根是x＝14.

本题原式为一个无理方程，解无理方程关键是要去掉根号，将其转化为整式方程.经过将等式两边平方后去掉了根号，得到了一个有理方程，再对等式两边进行移项后得到了方程的根.

例5解分式方程.

解：将分式去分母，两边同乘x-1，得

1-2（x-1）＝-3，

将等式两边去括号，得1-2x＋2＝-3，

移项后整理，得2x＝6，

解得x＝3，

经检验，x＝3 是方程的根，

所以x＝3 是原方程的解.

解分式方程最基本的思想就是将分式方程转化为整式方程.首先将方程的两边乘方程中各分式的最小公分母，通分去掉分母，将分式转化为整式方程.再进行去括号和合并同类项的运算，从而求得方程的根.这里要注意整式方程的解不一定是分式方程的解，但整式方程的解中一定包含了分式方程的解，因此要逐一检验所得到的整式方程的解，这个过程叫作验根，要检验求出来的根是否为原式的增根，增根是在把分式方程转化为整式方程的过程中产生的，要去掉增根才能得到原分式方程真正的根.

例6解二元一次方程组

解：令x＋2y＝9 为①式，3x-2y＝-1 为②式，

则①＋②得4x＝8，

解得x＝2.

把x＝2 代入①中，得2＋2y＝9，

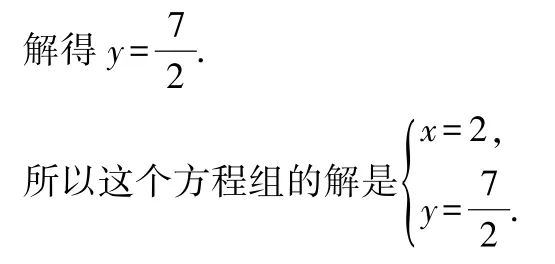
消元法是指通过有限次变换，消去原式中的某些元素.本题求二元一次方程组的解，利用加减消元法和代入消元法将二元一次方程转化为两个一元一次方程进行求解.这种将未知数个数由多化少，逐一求解的消元思想，同样也体现了数学的化归思想.

五、在一元一次方程的应用问题中体现的化归思想

实际问题与数学模型的转化思想是解决数学问题的关键.把实际问题转化成一个数学问题，这个过程被称为数学建模的过程.建构的数学模型要遵循简化原则、可推导原则、反映性原则，其具体步骤如下：

①审题明意：从阅读问题、理解问题的实际背景出发，看问题中一共涉及几个量，分析已知条件，明确各数量间的关系，然后概括出问题的数学实质.

②数学建模：找出能够表示实际问题中全部含义的一个等量关系，建立一个数学模型.

③问题标准化：将建好的数学模型转化为方程（组）、不等式组、函数等常规的数学问题，进而解决实际问题.

下面我们以解决实际问题中的商品打折促销问题的过程为例，来深刻体会实际问题与数学模型的转化中所渗透的化归思想.

例7某商店将某种数码相机按进价提高了35%后，打出“九折酬宾，再让利50 元运输费”的广告进行促销，结果这种数码相机每台仍可获利208 元.问：每台数码相机的进价是多少元？

解析：题目中涉及数码相机的进价、利润率、折扣、让利以及利润这几个量，然后找到本题的等量关系转化为数学模型：根据商品利润＝商品售价-商品进价，得到该相机的利润＝［进价＋（利润率×进价）］×折扣-让利-进价.

首先设每台数码相机的进价为x元，然后将已知量代入建好的模型后得到一个一元一次方程：（x＋0.35x）×0.9-50-x＝208，解得x＝1200，故每台数码相机的进价为1200 元.

实际数学问题的解决离不开数学建模，数学建模的本质就是构建适当的等量关系，使得原来的问题情境转化为容易解决的问题的方法，是化归思想的集中体现.数学教学的终极目的就是让学生能够实现将实际问题转化为抽象的数学模型并进行解释与应用.

六、在几何问题中体现的化归思想

解决初中数学的几何问题时，需要经常与转化思想相结合.在初中数学七年级上册人教版教材中的第四章为几何图形初步，第一节的内容就要求学生能够识别立体图形的展开图.在探求立体图形平面展开图时，教师让学生在头脑中想象出沿着立体图形的棱角适当剪开的过程，这是由抽象到具体、由立体到平面的转化过程.在几何这一部分的学习中还有很多地方也渗透了化归思想，例如，化曲为直的思想、合同变换的思想等.这些均能体现化归思想在初中几何中的重要地位.

例8如图2，圆柱形的玻璃杯高为14 cm，底面周长为32 cm，在杯内壁离杯底5 cm 的点B处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿3 cm 与蜂蜜相对的点A处，求蚂蚁从外壁A处到内壁B处的最短距离（杯壁厚度不计）.

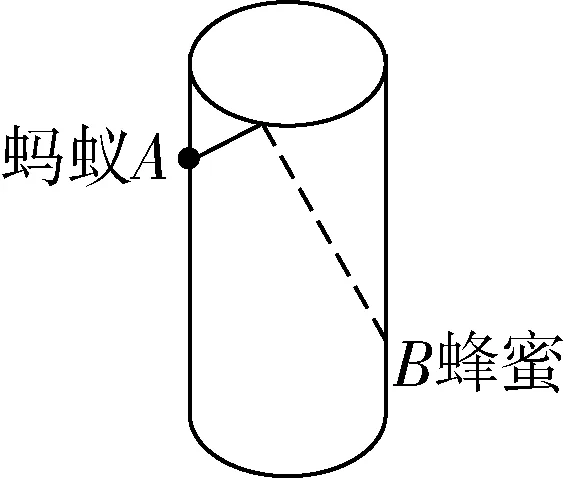
图2

解：如图3 所示，将该圆柱的侧面展开，点A′为点A关于EF的对称点，

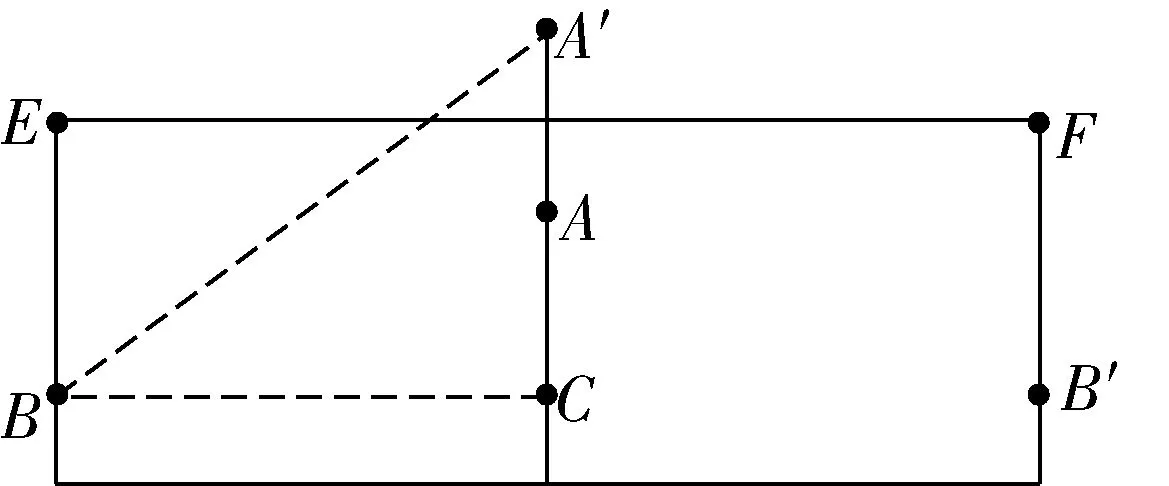
图3

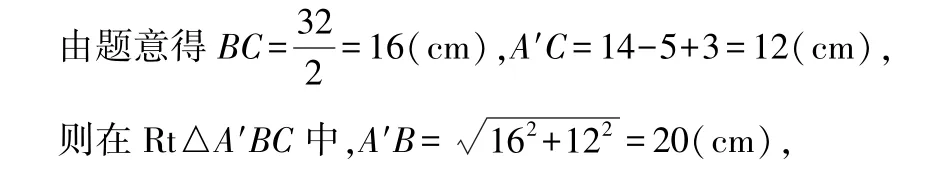
则蚂蚁从外壁A处到内壁B处的最短距离为20 cm.

本题的情景设置在一个圆柱形的物体上，圆柱的表面是曲面，如果直接去思考问题会很抽象，不易理解.但是，只要我们想象这个圆柱侧面展开后的样子，将曲面化为“直线”平面图形；将蚂蚁的运动轨迹由曲线变为直线.经过这样的转化后再对问题进行思考就会觉得清楚易懂了.运用化曲为直的思想能够训练学生的数学思维，培养学生的探究能力.

例9已知梯形ABCD中，CD∥AB，∠A＋∠B＝90°，M，N分别为AB和CD的中点，求证：MN＝.

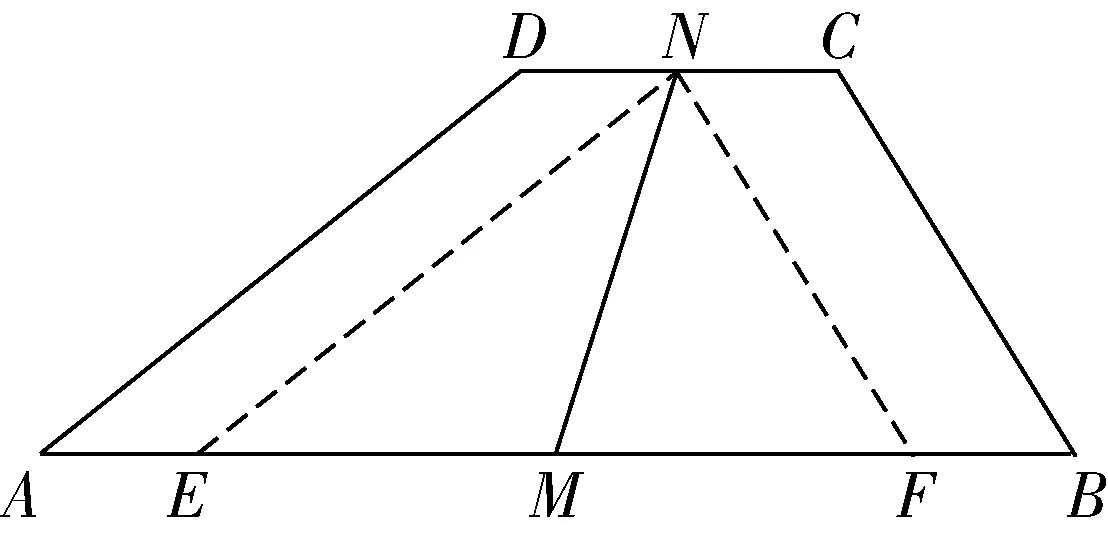
图4

合同变换的思想是指图形在进行平移、对称、旋转的变换下，与其本身全等的变换.本题的证明中首先过点N分别作NE∥AD，NF∥BC，交AB于点E，F，这也可以等同于NE是AD向右平移后的线段，NF是BC向左平移后的线段.因为∠A＋∠B＝90°，所以∠NEF＋∠NFE＝90°，所以两线段平移之后形成的△NEF是一个直角三角形.于是，解题思路就转化为证明MN为Rt △NEF斜边上的中线，又转化为2MN＝EF＝AB-CD，即可证明结论.合同变换思想在初中数学的平面几何中比较常见，所以也是要求学生能够领悟的一个思想方法.

七、在找规律问题中体现的化归思想

解答探索数学规律的问题时，我们要认真观察题目中给出的数字、式子或图形的变化规律，在阅读和观察的基础上理解其实质、方法和思想，再结合数字、式子或图形的特征和意义解题.这类问题的主要类型有：阅读和观察特殊范例，推出一般结论再运用；阅读解题过程，总结解题思路和方法，再进行运用；阅读新知识，研究新问题等.下面给出一道运用“阅读和观察特殊范例，推出一般结论再运用”的典型化归思想方法来解决问题的例题：

例10一个自然数的立方，可以“分裂”成若干个连续奇数的和.例如：23，33和43分别可以按如图5 所示的方式“分裂”成2 个、3 个和4 个连续奇数的和，即23＝3＋5；33＝7＋9＋11；43＝13＋15＋17＋19……若113也按照此规律来进行“分裂”，则113“分裂”出的奇数中，最大的奇数是什么？

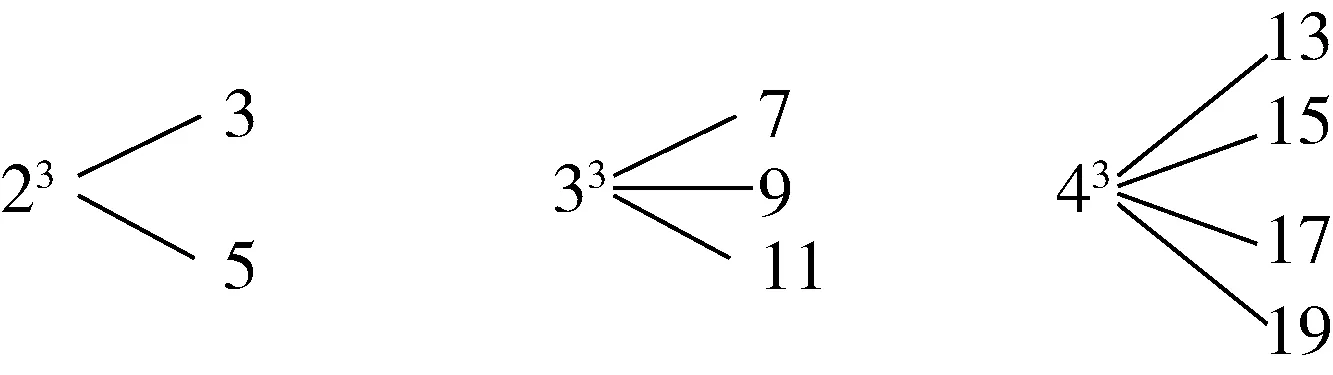
图5

解析：23＝3＋5，“分裂”的第一个数是3＝2×1＋1，33＝7＋9＋11“分裂”的第一个数是7＝3×2＋1，43＝13＋15＋17＋19“分裂”的第一个数是13＝4×3＋1，从而可知n3“分裂”出的奇数中第一个数是n（n-1）＋1.通过观察还可知，每组数的底数是几就“分裂”出几个奇数，又因为每两个相邻的奇数之间相差2，并且从第一个奇数往后数还有（n-1）个奇数，则n3“分裂”出的最后一个奇数是n（n-1）＋1＋2（n-1），故113按照此规律“分裂”出的奇数中，最大的奇数是n（n-1）＋1＋2（n-1）＝11×（11-1）＋1＋2×（11-1）＝131.

该例题的解题方法就是通过观察题目中给出的三个自然数的立方“分裂”的特殊的情形，总结出两个一般规律，即n3“分裂”出的第一个奇数n（n-1）＋1 和最后一个奇数n（n-1）＋1＋2（n-1），这是从特殊到一般的转化过程.总结出自然数的立方“分裂”的一般规律后，再将题目中所要求出的特殊值113的底数11 代入最后一个奇数n（n-1）＋1＋2（n-1）这个一般规律中求出最后结果，此过程为从一般到特殊的转化过程.

从特殊到一般的数学思考方式是化归思想中重要的一部分，也就是从特殊的事例中总结出一般规律的过程，这种数学思考方式就叫作从特殊到一般.从特殊到一般再从一般到特殊这种反复的认识过程正是人们认识事物的基本过程，在数学中也不例外，我们可以让学生充分发挥自己的探究能力，培养学生的数学思维，在认识数学的活动中起到重要的作用.

八、结束语

在初中数学教学中，有很多问题都蕴含着化归思想，灵活地运用化归方法能够帮助学生学习和理解各种数学知识.本文详细阐述了初中数学教学中的化归思想的内涵以及对典型的化归思想案例进行分析，希望可以为广大数学教师提供参考，促进我国教育事业的发展和进步.经过分析表明，无论是在有理数的运算、代数式的运算、解方程与解方程组的运算中，还是在方程的应用、几何的构成和变化的规律问题中，都有极其明显的体现.我们也可以清楚地看出化归思想的运用可以让解题思路更加灵活，让解题方法更加多样.这也更加印证了在数学教学中渗透化归思想的重要性.因此，教师在教学过程中应多挖掘、多思考培养学生化归思想的教学方法，让学生能够熟练掌握化归思想，使学生能够通过化归思想解决各种问题，培养学生自主学习、独立思考的意识，激发学生对数学学习的兴趣.