对苏州2020 年中考数学压轴题第28 题的思考——借题论数学转化思想的重要性

庄光新（苏州市工业园区朝前路实验学校，江苏 苏州 215125）

一、从心培育转化恐惧，引领数学人生观

中考最后一题是压轴题，只要学生听到这样的词语，无不从心理上产生深深的恐惧，畏惧心理严重.中考最后压轴题信息量大，题目长，数形阅读理解转移标记多，大多数中等学生经常在审题这一关就被卡在门外，从而无法深层地研究学习.久而久之，学生的综合分析能力就会大打折扣，挑战自我的信念严重下降.面对这样的教学实情，教师要从平时的点滴学习中，分解复杂，拆分试题，小层次递进，以小层次的成就感从心理上培养学生面对恐惧.慢审题、画关键、数形结合标参数、题目一次读不明白，再来一次，细品条件、慢悟关系、深入试题，对试题有一个熟悉的环境认识，增加亲近感.对于综合几个小问题的，学生虽然不能同时解决，但可以完成第一小问，并顺利得分，为中考总分添一分精彩.同时，学生要明白压轴题的小问是层层递进的，有着重要的承上启下的意图，往往是第一小问对下面的第二小问有引导作用，要从简入手，明白问题的引导性.不舍不弃，努力做到更好，这不仅是学习，也是一种人生态度：成功来自前期的点滴积累，当前期的努力日积月累到一定的量时，量变会产生质变，敞亮的人生自然水到渠成.从而灌输学生正确的人生价值观.让所有学生从学数学领悟做人生的道理.

二、试题是载体，化难为易，分解试题

基础教育中数学理论、数学思想、数学方法必须以试题为着手点、为载体，把教育目标中所蕴含的理论目标、意识形态落实到学生看得见、摸得着的实体数学问题中，数学离开具体的试题载体，什么思想，什么意识，什么方法都无立足之本，高谈阔论的专家教学不如让学生动笔实践的效果更实效.让学生从实际的试题出发：哪些话是有效的，哪些话是扰乱迷惑我们表象思维的，这些话中，关键词是什么？这两句话是什么意思？你能通过这两句话联想到什么与主题关联的隐性内容，这些内容对本题有没有用？比如，初三数学中，如果见到直角这个概念，我们要求学生必须联系到如下知识点：1：垂线段最短；2：垂直平分线的性质与“三线合一”；3：直角三角形以及勾股定理、圆中的垂径定理、设未知数组建勾股定理；4：构造圆并找到直径；等等.利用这些基础知识点关联题目，有用的重点关注，没用的先暂时放一边，你必须想到这方面的知识，由条件联想它的结论？求这个问题，等价于求另一个什么问题？这个问题无法直接解决，能不能“围魏救赵”先解决别的问题.这样的设疑能训练学生扩散思维，逐步培养学生由扩散思维转向聚焦思维，将某些正面问题转化为反面问题，从而从思想与行动上让解题更有效、更简单，思维更清晰明了，丰富学生的数学思维.比如，下面分析推理苏州2020 年中考题28 题的过程如下：

1.慢审题，标条件转化为自我语言表述问题

在具体审题时，做到慢审题速表达.学生读一句中文表达，就在图形中用自我熟悉的数学符号标识对应的数学条件，并对某个特定的条件瞬间联想某个相关联的结论，把问题条件内化为自我认识，拓展问题的联系性.学生最好能用自我的数学语言或者白话语言表示出来，或者动作形态展示题目的意思，转化陌生内化亲近，读不懂的地方反复读，品不全的地方再领悟，有没有条件遗漏的，遗漏条件将会直接导致解题无法进行.当学生卡住的时候，需要回头看，不能一味地死盯牛角尖.

如图1 所示，由角平分线OT和直角∠QOP，得∠1 ＝2 ＝45°，由同弧所对的圆周角，得∠1 ＝∠2 ＝∠3 ＝∠4 ＝45°.利用坐标系会有Rt△QOP，并联想直径QP，利用∠3 ＝∠4 ＝45°得到等腰直角三角形QCP，内接四边形QCPO，初步厘清各条件的作用与关联.这些条件要让学生结合图形直接表达，不能再依靠文字条件.数形结合是一种重要的理解能力的转化，即把文字语言转化为符号语言，更是对文字语言的深层次的理解，也是数学教学中必须坚持和长期训练学生重要环节.

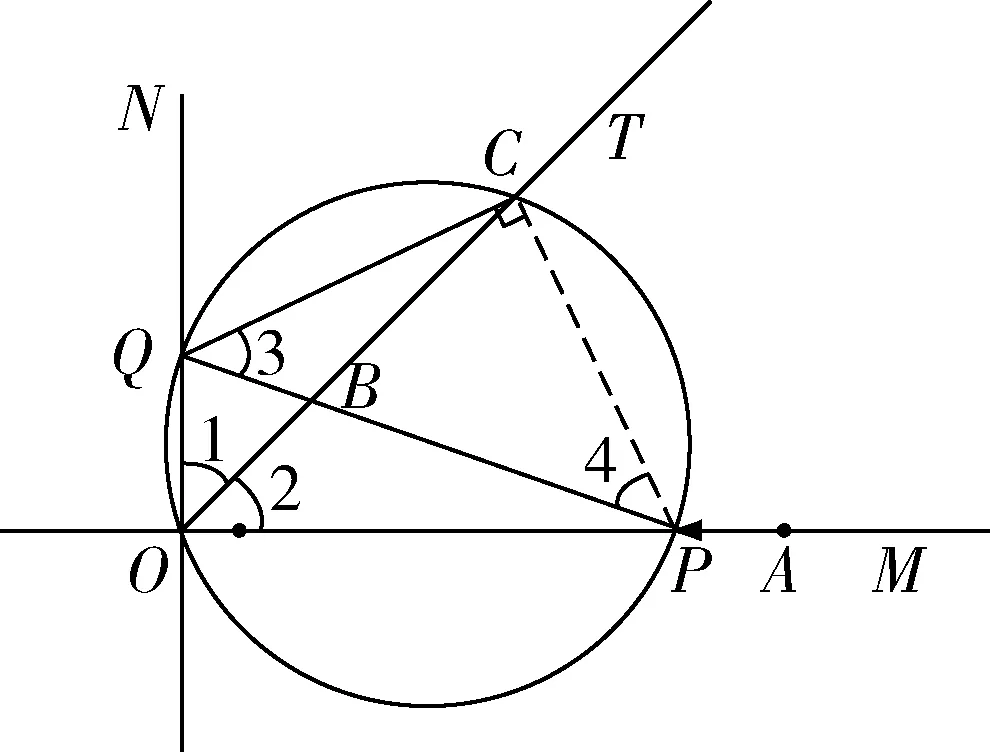
图1

2.动中有静，问题递进式转化问题

第一问：求OP＋OQ的值.

明确两个动点的方向、速度，标记Q的行程和P的行程和余程，因为P，Q的速度一样，而行程也一样，此时可把几何图形问题转化为代数模型问题，则PA＝QO，把几何问题转化为代数问题，可设SPA＝x，则SOQ＝x，OP＝8-x，所以OP＋OQ＝8 是一个定值，第一问轻易而解.但不能高兴太早，在移动的过程中，∠QOP永远是直角，QP永远是圆的直径，∠QCP也是直角，这些都是固化的定量.QP也是Rt△QOP所在圆的直径.△QOP和△QCP永远是直角三角形.变量有弦OC，弦OC无论怎么变最多和QP一样长，这些联想思维为第二问做铺垫.从而体现试题中小问引领的用途.学生要学会利用这种承上启下的引问过渡.

第二问：问OB的长度变化情况，有无最大？

师：可想而知，OB是弦OC的一部分，如果变化过程中OB变大，转化为BC会如何变化呢？

生：（猜测性地回答）变小.

师：那么BC最小的值在何方呢？为什么最小呢？

生：直角三角形中直角顶点到斜边垂线段最短（如图2所示）.

图2

引导学生正反思维，转移思路.在等腰直角三角形QCP中，BC是斜边的高时最小.

师：无独有偶，此时的OC是圆的什么呢？

生：直径.

生：∠2＝∠OCP＝45°，则∠OPC＝90°.

再深入探讨.

师：那此时∠OQC是多少度呢？

生：90°.

师：那么此时的四边形OQCP是什么图形呢？

生：正方形.

师：那么OP＝OQ了，而由第一问，OP＋OQ＝8，可得OP＝4，则此时的t等于多少呢？

生：4 秒.

详细解答过程：

当OC是圆的直径时，OB最大.

此时，∠OQC＝90°＝∠QOP＝∠QCP，

且∠1＝∠2＝∠3＝∠4＝45°，

则QC＝PC，

故四边形OQCP为正方形，

所以OQ＝OP.

由第一问OQ＋OP＝8，得OP＝4，

则PA＝4，

故t＝4÷1＝4.

综上所述，在第二环节的思维过程中，通过层层疑问，层层递进转化，我们将正向问题OB的大小转化为BC的大小研究.使问题限制在等腰直解三角形QCP中，从而使动态研究变成静态研究.完全把二次函数的复杂计算（见官方答案）转化为学生的分析推理，简化了大量的计算，锻炼了学生的思维，把转化的数学思想提升了一个质的高度.虽然这样的解答并非中考出题者的真实意图，但在教学中，教师偶尔以异样的思维与常态化思维进行对比教学，更能促进学生多思考，多创新.在以求同思维为基础上开拓个性的求异思维，把转化的数学思想深耕于学生知识能力体系中，并引领学生在以后的生活中，遇到困难也要学会利用外部环境，转化现实困难，做一个积极正向的健康人.

3.淋漓尽致的转化，斩断“老太婆的裹脚布”

中考的压轴题到了最后，如果不用辅助线，这首先在老师的心理上都是难以想象的，绝大多数教育者在这点都跳不出这个辅助线的思维定式，更何况学生呢？这种惯性思维严重扰乱了学生的开放思维.某种形式上固化了学生创新意识形态——辅助线捆绑我们的创造思维.2020 年苏州中考最后一题却反其道而行之，在辅助线配合相似与几何问题转化代数问题上做了大量的研究，它突破我们的常规思维，把问题的开放性与固化思维的定向选择性展示给老师和学生，从而引领老师日后的数学教学方向——多样选择，同时，让学生在几何、代数和整合性方面做出判断，不同的选择会得到不同的优化结果，虽然都能得出正确的答案，但所付出的思维价值及收获的思维喜悦成果却完全不同：一个烦琐陈杂，一个轻松简洁.出题团队站得高，看得远，最后一道试题的解答方案所包含的教学意识对今后老师的教学导向意图明显：殊途同归，精彩之余另有一番愉悦的数学体验.以试题为载体，求异、高效体验引领我们的教学方向——求异转化思想.让老师的教学思想开辟了一个新的方向.

第三问：要求四边形OQCP的面积（如图3 所示），此题运用几何转化代数的思想更是数学思维的精彩体现.在这一问上淋漓尽致地体现了转化的思想，彻底斩断数学思想中“老太婆的裹脚布”.分析如下：

图3

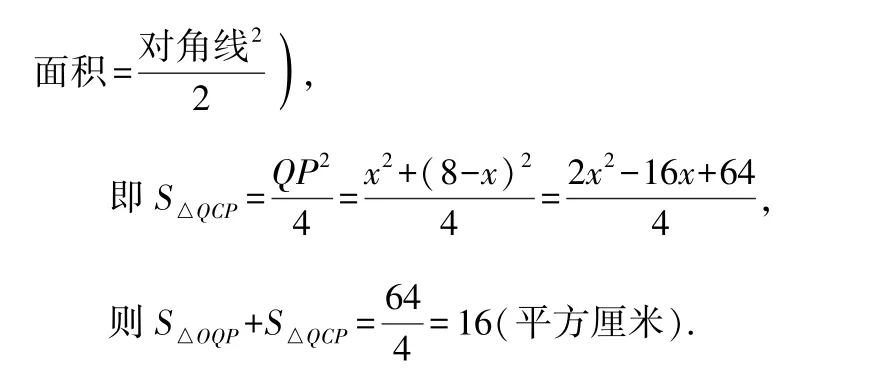
几何问题代数化的转移思想，整体代入，为求而不求，不仅分析简单化，而且计算轻巧便捷.运用这样的思维方式解题和2020 年苏州中考试题最后一题官方答案相对比，简捷很多.不同的学生有不同的思维，我们不能要求所有人都认同自己的观念或者自己的想法，但让学生从对比中领悟各种数学思想的优劣性，取其优点，在对比中，领悟转化的数学思想的奇效性.如果这个思想能为学生学习提供更高的效率就选择使用，一切在准确的基础上，再讲效率，讲策略性，不断优化学习方法，使其学习绩效更优化.最终让教育者数学教学的意识形态与学习者的数学学习绩效不断整合、共同进步，为培养创造性人才奠定坚实的基础.

到此为止，2020 年苏州中考试卷的最后一道压轴题就这样“轻而易举”的顺利完成，书写形式简洁，逻辑思维流畅，化难为易的转化手段高效.没有辅助线，没有函数知识，没有大量的计算，没有整版的书写，学生学得轻松，答得容易，理的清晰，学的开心，领悟颇多.究其原因，就是我们在其中运用了大量的转化思想的教学手法.书写表达上简洁了，但我们的思维训练的难度增加了，无形的逻辑推理分析大大促进了学生的思维训练，真正体现了数学学习的本质.

三、结束语

数学转化思想是数学思维中重要的一个组成部分，一要转化学生的恐惧心理，分解试题，小步骤前行，让学生慢慢体会成功的喜悦，并为前进提供情感动力.二要转化学生的解题思维.当然，这道压轴题是一个特殊典型题.数学教学中思想方法还很多，需要我们平时用心，并用独特的教育思想去引领学生发现创新，通过长期的教育培养，以试题为着手点，培养学生的转化问题的意识，并把这种意识带入学生的生活学习中，当学生遇到问题、难题、难事时，能转移一下视角、换个方向.条条大路通罗马，但智慧的驾驶者可能在奋斗的道路上事半功倍.希望转化的数学思想能为学生的学业提升提供一个高效的手段，同时希望学生在以后的日常生活中，能积极转化自己生活中遇到的困难，做一个积极正向的健康人.