日本东京版教材《乘法分配律》一课教学设计与意图

文|柯 媛

【教材内容简介】

《新算数》（日本东京版）《乘法分配律》一课内容安排在四年级下册第一单元《运算的规则》中的第2课《计算的程序》。本课教材内容主要包含四个环节：1.观察计算两种颜色圆片的总个数，红圆片有11行，蓝圆片有4行，每行都是8个；2.用符号表征乘法分配律，并代入具体的数验证等式成立；3.由乘法分配律类比出除法分配律，并代入具体的数验证等式成立；4.运用乘法分配律对算式109×5和98×6进行简便运算。

【全课设计说明】

通过教材研读与分析，日本东京版《乘法分配律》一课有如下特点：1.以纯数学情境引入，列出综合算式，有利于学生发现规律；2.在规律探索时，注重引导学生经历“猜想—验证”的推理过程，发展推理能力。

基于以上思考，本课教学设计将关注以下两个方面：1.借助直观图形，引导学生发现规律，并借助符号■、●、▲来表示规律；2.在验证规律时，除了用具体的数，鼓励学生运用其他方法，如列举生活实例或者画图来验证结论成立。

【教学目标】

1.通过学生独立思考、小组交流、全班汇报探索发现乘法对加减法的分配律成立，进而拓展到除法对加减法的分配律也成立，提高学生猜想、验证等能力。

2.让学生经历规律探索及“观察—猜想—验证—结论”的推理过程，培养学生推理的能力和严谨思考的习惯，同时积累合情推理的数学活动经验。

3.能够运用乘法分配律，对一些算式进行简便运算，体会计算方法的多样化，发展数感。

【教学重点】

探索发现乘法对加减法的分配律是成立的，除法对加减法的分配律也是成立的，并能用具体的数、列举生活实例或者画图进行验证。

【教学难点】

理解四种分配律的意义，发展推理能力。

【教学准备】

课件、《学习单》（每人一份）。

【教学过程】

一、情境引入（教材译文片断如下）

出示教材中的情境，引导学生独立思考并解决问题，给学生充分的学习时间，要求学生有几种方法写几种，并思考每种方法是怎样想的。

（学生独立完成《学习单》第1题）

【设计意图：通过引入一幅“多个圆形”组成的图，创设纯数学情境，类似点子图，减少干扰；同时在列式上要求“列一个式子来解答”，即要求列出综合算式，这样有利于学生得出用于比较的等式，便于发现规律。】

二、规律探索

1.初步发现规律。（教材译文片断如下）

（1）学生独立完成后，组织全班交流，要求讲清楚是怎样想的，算式是什么，感受方法多样化。

预设1：（11＋4）×8＝120（个），用红圆片和蓝圆片的总行数乘每行的个数。

预设2：11×8＋4×8＝120（个），分别计算红圆片和蓝圆片的个数，再相加。

（2）比较两个算式的结果，引导学生发现：上面两个式子表示相同的大小，因此可以用等号连接，进而得出等式：（11＋4）×8＝11×8＋4×8。

预设：这两个算式是同一个问题的两种解法，结果都是120，所以这两个算式结果相等，但算式表示的意义不同。

（3）引导学生观察等式左右两边算式的特点，看看有什么发现。

预设1：两边算式中都有相同的乘数8，都有乘法和加法两种运算。

预设2：左边是合并算，右边是分开算。

预设3：两个数的和与一个数相乘，可以将这两个数分别与这个数相乘，再相加。

【设计意图：结合解决问题的过程，借助图形直观，抽象出两个算式，引导学生交流两种不同列式计算的方法，感受等值变形的特点，初步发现规律，同时通过部分学生的语言表述来逐渐认同规律。】

2.猜想和验证乘法对加减法的分配律是成立的。（教材译文片断如下）

（1）用符号■、●、▲代表三个数，写出上面发现的规律。

（学生独立完成《学习单》第2题）

预设：（■＋●）×▲＝■×▲＋●×▲

（2）进一步追问：如果将式子中的加号都换成减号，还成立吗？

预设：成立。（■-●）×▲＝■×▲-●×▲

（3）这两个式子是否成立还不知道，现在只是猜想，还需要进一步验证。

（4）独立思考，想办法验证上面的等式成立或不成立。学生先独立计算，再全班汇报，大家共同判断。

预设：用具体的数，将■＝4，●＝3，▲＝2代入上面的两个式子计算，看等号两边的得数是否相同。（4＋3）×2＝4×2＋3×2，（4-3）×2＝4×2-3×2。因此，上面的两个等式都是成立的。

（5）鼓励学生再多写几组数代入计算，发现等号左右两边的计算结果相等。同时鼓励学生运用其他方法，如列举生活实例或者画图来验证结论成立。

预设1：列举生活实例。妈妈在超市买了2千克苹果和3千克桃子，苹果和桃子的单价都是9元，计算两种水果的总价，用两种不同的方法计算，可以得到（2＋3）×9＝2×9＋3×9。

预设2：画图。有两个不同大小的长方形（长3宽4、长7宽4），计算两个长方形的面积之和，用两种不同的方法计算，可以得到（3＋7）×4＝3×4＋7×4。

（6）向学生揭示规律并完善板书。

（■＋●）×▲＝■×▲＋●×▲乘法对加法的分配律

（■-●）×▲＝■×▲-●×▲乘法对减法的分配律

【设计意图：至此，完成了用语言到符号表达的过程，揭示出乘法对加减法的分配律，让学生体会用符号表示运算规律的简洁性和优越性。同时让学生用具体的数、举生活实例、画图等方法验证猜想，有利于让学生验证乘法分配律的正确性，也有利于培养学生独立思考、严密推理的能力。这也为下一步类比推理提出除法分配律的猜想奠定了基础。】

3.猜想和验证除法对加减法的分配律也是成立的。（教材译文片断如下）

（1）除法对加减法是不是也有分配律？如果有，请你写一写除法对加减法分配律的符号表达式，同时想办法验证除法对加减法的分配律是成立的。

（学生独立完成《学习单》第3题）

预设1：学生会把乘法分配律中的乘号换成除号，形成除法分配律的猜想。

预设2：学生会用刚才学过的三种方法来验证除法分配律成立。

（2）以四人小组为单位交流。

①交流前，先独立思考，保证在交流时有话可说。

②交流时，大胆表达个人见解，认真倾听组内同学的想法。

③交流后，每个组推荐一名代表向全班汇报。

（3）组织小组汇报，教师注意启发学生的互动，让学生之间、小组之间进行补充和追问。汇报时，要求学生说清楚结论和理由。

预设1：用具体的数。将■＝9，●＝6，▲＝3分别代入上面的两个式子进行计算，看等号两边的得数是否相同。（9＋6）÷3＝9÷3＋6÷3，（9-6）÷3＝9÷3-6÷3。因此，上面的两个等式都是成立的。

预设2：列举生活实例。小红有20颗糖，小华有30颗糖，把两人的糖平均分给10个小朋友，每个小朋友可以分到几颗糖？用两种不同的方法计算，可以得到（20＋30）÷10＝20÷10＋30÷10。

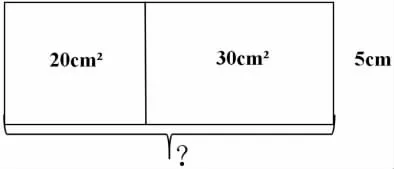
预设3：画图。求大长方形的长，用两种不同的方法计算，可以得到（20＋30）÷5＝20÷5＋30÷5。

（4）教师根据学生的回答完成板书，并揭示规律。

（■＋●）÷▲＝■÷▲＋●÷▲除法对加法的分配律

（■-●）÷▲＝■÷▲-●÷▲除法对减法的分配律

【设计意图：首先，运用已有的乘法对加减法分配律的知识，以及乘法与除法的关系，类比提出除法对加减法分配律的猜想，有利于培养学生类比推理的能力，同时有利于学生形成知识的闭环，帮助学生感受知识的连贯性，加深对分配律的理解。其次，让学生经历从猜想到验证的过程，培养学生逻辑推理的能力和严谨思考的习惯，同时积累合情推理的数学活动经验。在此过程中，教师应尊重学生个性化的想法，只要表达清楚，说出依据，都应该鼓励，让学生在说理过程中再次体会和理解发现的规律。】

三、巩固应用（教材译文片断如下）

1.先让学生观察这两个算式的特点，想一想，可不可以运用乘法分配律进行简便运算，再让学生思考简便运算的思路，在《学习单》上尝试写出过程。

预设：可以将109和98都拆成两个数的和，再运用乘法分配律分别进行计算。

2.完成后，引导学生充分交流算法，鼓励学生说清楚简便运算的想法与过程，教师追问：哪里可以看出能进行简便运算？算完后，可以再一起用原来的运算顺序算一算，看看有什么发现。

预设1：109×5＝（100＋9）×5＝100×5＋9×5＝500＋45＝545。

预设2：98×6＝（100-2）×6＝100×6-2×6＝600-12＝588。

预设3：运用乘法分配律计算比用竖式计算更简便，更省时。

【设计意图：这两道练习题都是乘法分配律的正向运用，需要先对109和98进行拆分，变成（100+9）和（100-2），再分别运用乘法对加、减法的分配律进行计算。侧重让学生经历分析算式特点、主动运用规律灵活计算的过程，加深对乘法分配律价值的感受，逐步培养学生的简算意识，提升学生简便运算的能力。】

四、回顾总结

1.过程回顾。

解决问题得出等式——猜想和验证乘法对加减法的分配律成立——猜想和验证除法对加减法的分配律成立——应用分配律进行简便计算。

2.结果回顾。

（1）乘法对加减法的分配律成立。

（2）除法对加减法的分配律成立。

3.你还有什么疑问？

【设计意图：通过对教学过程和所学知识结果的回顾，帮助学生理清知识的来龙去脉，培养学生归纳概括的能力和总结梳理、反思修正的习惯，加深学生对四种分配律的整体印象，从而有助于学生掌握知识的重点和知识的系统性，使得新知识具有更大的迁移价值，为后继学习和运用它们奠定基础。】