中国北师大版教材《乘法分配律》一课教学设计与意图

文|陈绮琳

【教材内容简介】

北师大版《乘法分配律》一课的内容安排在四年级上册第四单元《运算律》中的第6课《乘法分配律》，分为两个课时进行教学，第一课时是对规律的探索与验证，第二课时是乘法分配律的简算教学，本文介绍的是第一课时。教材包含三个部分：情境创设、概念呈现以及解释规律。第一部分：情境创设，出示了装修师傅贴厨房瓷砖的情境图，已经铺好的瓷砖可以分为两种角度观察。这部分包括两个问题：1.贴了多少块瓷砖？说说你是怎么算的？呈现了四个不同的综合算式，分成两组算式。2.观察上面两组算式，你有什么发现？第二部分：概念呈现，提出问题：用a、b、c代表三个数，你能写出上面发现的规律吗？出示了乘法分配律的数字和字母表示。第三部分：解释规律，要求学生结合4×9+6×9这个算式说明乘法分配律是成立的。出示了点子图与乘法的意义两种方法解释乘法分配律的意义。

【全课设计说明】

通过教材分析，北师大版《乘法分配律》一课有如下特点：1.以瓷砖（方格）引入，有利于学生在图形直观中建构规律模型；2.新课引入、探究规律、解释规律一共提出四个问题，积累学生发现问题和提出问题的经验，让学生尝试用自己的语言描述规律；3.唤起学生的已有经验解释规律的正确性，降低学习乘法分配律的难度，更好地理解规律。

基于以上思考，本课教学设计将关注以下几个方面：1.结合情境方格图，借助图形表征（面积模型），由易到难，建构规律模型；2.补充概念呈现的文字描述，帮助学生梳理规律在脑海中的记忆与提取；3.结合学生的已有经验，凸显乘法意义表征，唤起学生的已有经验解释规律的正确性，理解乘法分配律的本质意义。

【教学目标】

1.通过“铺瓷砖”情境，经历探索、发现乘法分配律的过程，尝试用文字表述乘法分配律，会用字母表示乘法分配律，培养分析、推理、抽象、概括等思维能力。

2.通过观察、对比、分析、猜想、验证等活动，积累提出问题、发现问题、解决问题的经验。

3.结合学生的已有经验，借助生活例子、乘法意义与图形直观建立规律模型，理解乘法分配律的意义。

【教学重点】

引导学生用数学的思维方法探索发现乘法分配律，借助乘法意义与图形直观建立规律模型。

【教学难点】

归纳乘法分配律并理解其意义，拓展规律。

【教学准备】

课件、情境图挂件、练习纸一。

【教学过程】

一、创设情境，初探规律

1.上课开始，教师出示下面问题：

淘气家在装修，工人师傅已经铺好了一部分，（教师在黑板上贴情境主题图）一共贴了多少块瓷砖？要求学生用综合算式解决问题，如果已经用一种方法解决了问题，再尝试用不同的方法解决问题。

2.学生独立思考解决问题。

3.全班交流。

要求学生汇报：（1）列出的算式与结果；（2）算式中每一步计算的含义。

预设方法1：白蓝两色的瓷砖一起算，（3+5）×10=80（块）。先求出白色与蓝色瓷砖有3+5行，每行10块，所以是（3+5）×10=80（块）。

预设方法2：先分别求出每种颜色的瓷砖，再相加，3×10+5×10=80（块）。白色瓷砖为3×10块，蓝色瓷砖为5×10块，然后把它们加起来就是总数。

预设方法3：两面墙的瓷砖一起计算，（4+6）×8=80（块）。先求出一行瓷砖有4+6块，有8行，所以是（4+6）×8=80（块）。

预设方法4：先分别求出每一面墙的瓷砖，再相加，4×8+6×8=80（块）。左面墙为4×8块，前面墙为6×8块，然后把它们加起来就是总数。

4.让学生观察这四个算式，提出讨论的问题：哪两个算式联系紧密？理由是什么？是否可以用等号连接？

预设：（3+5）×10=80与3×10+5×10=80联系紧密，都有3、5、10这三个数。（4+6）×8=80与4×8+6×8=80联系紧密，都有4、6、8这三个数。

5.为什么（3+5）×10=3×10+5×10，（4+6）×8=4×8+6×8？

预设理由1：因为左右两边计算出来的结果都等于80，所以相等。

预设理由2：教师引导学生从乘法的意义去理解：

（1）因为左边是3+5个10的和，也就是8个10的和，右边是3个10的和与5个10的和相加，也就是8个10的和，所以（3+5）×10=3×10+5×10。

（2）因为左边是4+6个8的和，也就是10个8的和，右边是4个8的和与6个8的和相加，也就是10个8的和，所以（4+6）×8=4×8+6×8。

【设计意图：北师大版“铺瓷砖”是数形结合的生活场景图，学生结合瓷砖方格说式子的意义，数形结合帮助学生观察发现乘法分配律的形式。学生通过找有联系的两个算式，感受等值变形的特点，初步发现规律。教学时借助乘法意义，沟通新旧知识的联系，初步理解乘法分配律的本质。】

二、想象列举，概括规律

如果工人师傅继续铺瓷砖，类似这样的等式还有吗？你能列举出来吗？

1.学生独立思考完成《练习一》。

2.全班交流。

挑选三个具有代表性的学生作品汇报，要求学生汇报：（1）结合填空与所画的图，说说等式左边与右边表示的意义；（2）观察三组等式发现的规律。

预设：（1）等式左边先算加法再算乘法，等式右边先算乘法再算加法；（2）等式左右两边都用到三个数；（3）等式左边有括号，右边没有；（4）等式左边只有两步计算，右边有三步计算。

3.教师适时帮助学生归纳、概括规律：可以怎样概括等式左边的特点？右边呢？

教师小结：两个数的和与一个数相乘，可以先把它们与这个数分别相乘，再相加，这就是乘法分配律。

4.教师利用板书上的等式解析分别相乘的意思，并用箭头符号表示，完成板书。

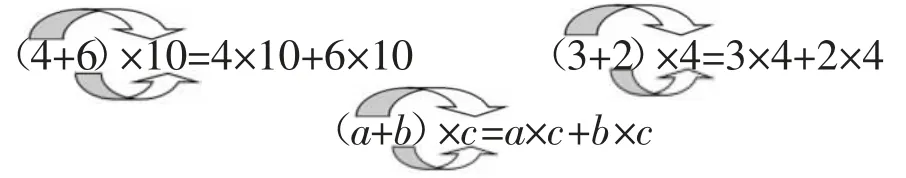
5.同桌交流：什么是乘法分配律？

6.文字和字母表示这个规律，哪种更简洁？用字母表示的式子为什么左右两边会相等？

预设：（a＋b）个c等于a个c加上b个c，所以（a+b）×c=a×c+b×c。

【设计意图：在继续铺瓷砖中想象列举类似的等式，丰富学生建模的过程，形成模型的表象。学生在独立思考与合作交流中，强化乘法意义表征与面积模型建构，探索发现规律，积累从特殊到一般的归纳推理能力。用语言描述模型的特征，能加深学生对模型结构的理解，对训练学生的数学思维能力非常重要。引导学生比较字母式与文字表达二者之间的优劣，让学生体会字母模型的优越性。】

三、面积模型，拓展规律

1.用面积图形表示（a+b）×c=a×c+b×c。

教师用课件演示，先求大长方形的长是（a＋b），（a+b）×c是大长方形的面积，左边长方形的面积等于a×c，右边长方形面积等于b×c，左边长方形面积加右边长方形面积等于a×c+b×c，所以（a+b）×c=a×c+b×c。

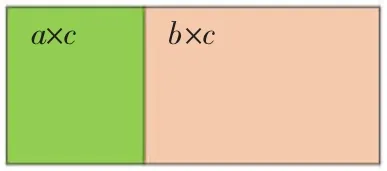
2.乘法分配律是乘法对两个数的和的分配律，乘法对三个数的和有分配律吗？乘法对四个数的和、五个数的和呢？

用面积图形表示（a+b+c）×d=a×d+b×d+c×d

【设计意图：从方格子模型自然演变到面积模型，充分利用面积模型的直观对乘法分配律进行拓展，学生容易接受。拓展规律有助于培养学生的思维品质。】

四、巩固练习，应用规律

练习1：当“医生”判断正误。

（1）30×（6+4）=30×6+4（）。

（2）（26+5）×7=26×5+26×7（）。

（3）63×63+37×63=（63+37）×63（）。

练习2：结合图与同伴说说等式3×6＋4×3＝（6＋4）×3为什么成立。

练习3：什么是乘法分配律？请用字母表示。

师：你能用生活中的例子解释一下乘法分配律的意思吗？

【设计意图：练习1辨识乘法分配律，进一步强化乘法分配律。练习2是北师大版教材的一道配套练习题，数形结合突出合并算必须要符合：只有相同的边相拼，才可以“合并求”小正方形的总数。练习3是根据教材解释规律部分改编而来的，在前面部分学生已经用面积模型和乘法意义解释规律了，用故事情境表征的方式，帮助学生将乘法分配律运用到生活中解决问题，提取乘法分配律在北师大版二、三年级教材的渗透内容。】

五、小结提升，提炼思想方法

1.回顾方法。

师：想一想，我们这节课学习了什么运算律？我们是通过什么方法帮助理解它并验证它的成立？

根据学生发言教师引导得到板书：方法：乘法意义、面积图形、举生活例子。数学思想：归纳、联系、数形结合。

2.大胆猜想。

师：我们学习的乘法分配律是乘法对加法的分配，你觉得乘法对减法有分配律吗？对于分配律你还有什么大胆的猜想吗？你打算怎么验证你的猜想呢？

预设：学生猜想除法对加法是否有分配律，乘法对两个数的和再减一个数的差是否有分配。

【设计意图：通过回顾学习帮助学生提炼数学学习思想方法，打通乘法分配律多元表征的融会贯通，猜想激发学生对运算律探究的欲望。】