基于分类车头时距的城市道路大型车影响分析

李君羡，沈宙彪，童文聪，吴志周*

（1.同济大学，道路与交通工程教育部重点实验室，上海 201804；2.上海市城市建设设计研究总院（集团）有限公司，上海 200125）

0 引言

我国城市物流发达，吸引大量大型车交通，对城市道路尤其是边缘区与中心区的衔接通道运行效率造成影响，量化该影响对制定大型车管控策略意义重大。

国外学者多在高速公路场景中研究大型车对混合交通流的多元影响[1]以及大型车与邻近车辆的相互关系[2]，其成果难以供城市道路管理借鉴。国内学者更多聚焦于城市道路，其中，因车头时距可全面反映交通流微观运行情况[3]，被广泛选用为分析指标。车头时距曾经难以获取，故早期研究多依赖人工调查数据或理论建模：邵长桥等[4]基于少量数据论证信号交叉口排队车头时距可用单对数正态分布拟合；赵星等[5]结合理论公式拟合大型车对车道设计通行能力的修正系数；YU等[6]在经典模型的基础上得到车头时距理论模型，探讨车道数、车道宽度等因素对理论通行能力的影响，并基于实地调研数据验证了模型效用；王益等[7]采用双因素方差分析法提出了考虑大车比例与车道宽度两个因素交互影响的饱和流率修正理论模型。随着智能交通系统数据采集终端的密集建设与功能升级，以往人工调研数据时间覆盖范围有限、样本量不足、精确性欠佳等问题得以解决，同时，数据驱动成为评估城市道路运行情况的重要手段，其特征在于规避了诸多理想假设和复杂的建模过程。陶鹏飞[8]等基于自动采集数据论证了混合分布模型对车头时距分布的拟合精度优势。在各类数据中，车牌识别(LPR)数据被认为有较大应用价值[9]。邢韵等[10]基于LPR数据研究了饱和、非饱和车流的车头时距划分阈值，但未细化车型，故不支持大型车影响评估；王殿海等[11]提出基于LPR 数据的混合交通流饱和流率实时估计方法，验证了交叉口饱和车头时距可以二分支高斯混合模型描述，在区分小型车、大型车的基础上估计了混合车道的饱和流率，对比实测结果，误差较小，但其实例验证仅针对连续交叉口的1条车道，不仅未对路段和交叉口进行区分，也无法体现交叉口不同功能车道的车头时距分布差异。

综上，目前鲜有研究基于大量样本数据，区分路段与交叉口、区分交叉口车道功能拟合不同过车类型的车头时距分布，全面分析大型车对城市道路交通的影响。本文借鉴文献方法，以车头时距为指标，利用真实LPR数据分别分析大型车对城市路段和交叉口运行的影响。首先，按照连续过车的前、后车种类将过车划分为4种类型，基于大量LPR数据对每类过车在路段、交叉口的车头时距分布分别建立数个混合模型；然后，以最大期望(Expectation Maximum，EM)算法求解各模型参数；之后，结合Kolmogorov-Smirnov (K-S)检验、赤池信息准则(Akaike Information Criterion，AIC)与最小描述长度(Minimal Description Length,MDL)对模型择优；最后，在对比分析模型特征的基础上，考察大型车在不同车道条件下对城市交通运行的影响。

1 数据采集与预处理

LPR 按采集位置分为路段LPR 和交叉口LPR两类，分别由布设于路段的卡口设备及布设于交叉口的电子警察设备自动获取。单条LPR 数据关键字段如图1所示。

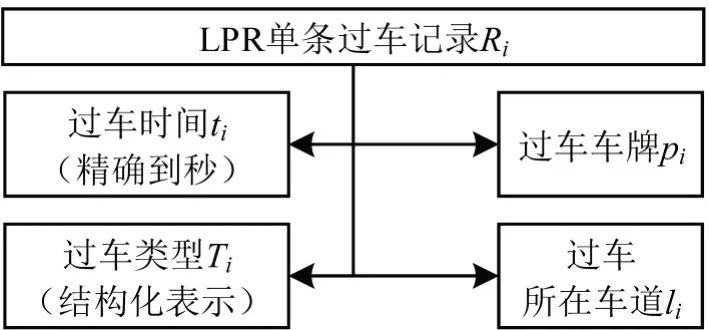
图1 LPR单条记录的关键字段Fig.1 Key attributions of each LPR record

两类LPR 对应车道功能及受信号控制影响不同，预处理方式存在差异，但基础步骤一致。

Step 1 对过车子类按车型尺寸合并为小型车、大型车，分别以c、v 表示，即Ti∈{c ,v} 。

Step 2 按照li汇聚同车道l的过车记录，构成集合Cli并按ti由先至后排序。

Step 3 对每个Cli,为每条Ri增加字段Ti(pre)=Ti-1(i≥2)，记录其前序过车类型。

Step 4 对每个Cli,为每条Ri增加字段hi=ti-ti-1(i≥2)，记录当前车辆与前序车辆之间的车头时距。

两类LPR后续处理步骤不同。

(1)对于路段LPR，设备点位与交叉口距离通常超过300 m，车道通行能力和驾驶人车道选择行为不受交叉口影响，即各车道过车组成、驾驶行为无差异；数据因设备故障等原因存在噪音。进一步处理如下：

Step5-seg对路段LPR所有Cli数据取并集生成路段过车记录集合C(seg)，按字段组合将其划分为4 个子集，分别对应4 类连续过车的先后关系组合“(过车组合”)记录，即[c,c]、[c,v]、[v,c]及[v,v] 。将其统一记作形式，其中，，β=Ti。

Step 6-seg 按照四分位异常数据判别方法[12]对各限定阈值后剔除异常数据。

(2)对于交叉口LPR，数据所在车道功能各异，且受到对应相位影响，车头时距并非完全由自然过车形成。进一步处理如下：

Step5-int对交叉口LPR所有Cli数据取并集生成交叉口过车记录集合C(int)，按车道功能将其化分为2 个子集，记作C(int-d),d∈{L ,S} ，其中，d为车道功能，L 为左转，S 为直行。因右转车道一般不受信号控制，故本文不做研究。

Step 6-int 按照Step 5-seg方法将各C(int-d)再分别划为4个子集，记作。

Step 7-int 对比信控方案，剔除各中hi大于对应相位红灯时长的记录，以排除因过车稀疏导致的极端值干扰。

2 建模与求解

式中：fi（x）、ωi为混合分布第i个密度分支及其混合系数；n为密度分支个数。

求解f（x）的关键技术包括：(1)确定fi（x）分布类型及n的候选值，以生成多个混合分布；(2)求解各混合分布的fi（x）和ωi；(3)择优模型。具体如下。

(1)拟合城市道路车头时距混合分布通常使用高斯分布[11]、对数正态分布[4]作为密度分支，故本文选择GMM、对数正态混合模型(Lognormal Mixture Model, LMM)、高斯/对数正态混合模型(Gaussian/Lognormal Mixture Model，GLMM)这3类模型分别拟合数据。鉴于两个基础分布的密度函数分别可用变量、变量对数的均值μ和标准差σ表示，将fi（x）统一表示为fi（x）=f(x;μi,σi)，其中，μi和σi分别为第i个密度分支的参数。

(2)考虑到EM算法简单、稳定的优势及其在类似研究中的效用[8,11]，以其迭代求解各混合分布的参数集Φ={ω1,ω2,…,ωn;μ1,μ2,…,μn;σ1,σ2,…,σn} 。

Step1 初始化参数集Φ（1），可参考数据特性人为干预，提升迭代速度。

Step 2 E 步骤，计算第j个样本在第M次（M ＞1）迭代中隶属于第i个密度分支的概率，即

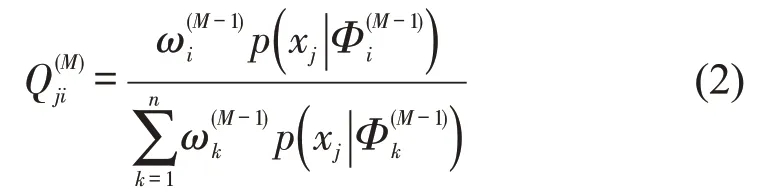
Step 3 M 步骤，结合全部N个样本，以评估Φ（M），即

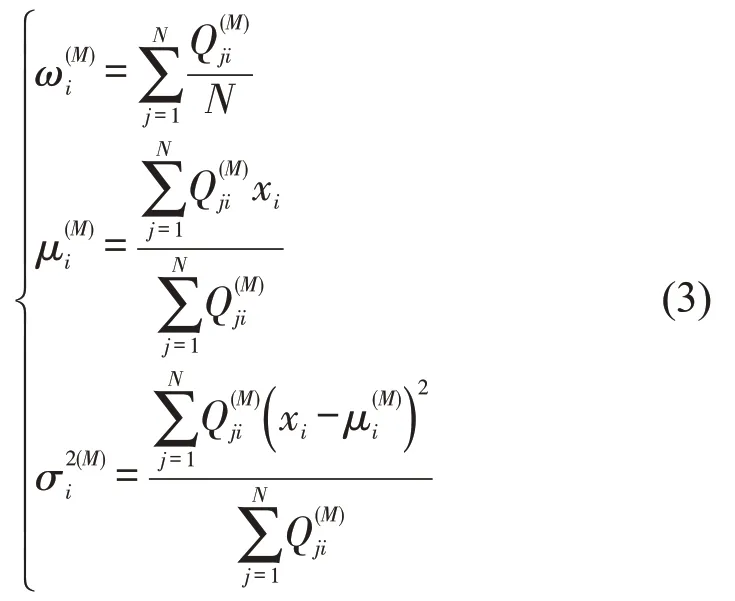
Step 4 交替进行E 步骤和M 步骤，直到Φ收敛。

(3)结合样本量及置信度，以K-S 检验排除(2)中拟合优度不符合要求的混合模型；对剩余模型，结合AIC和MDL准则择优。

(4)根据最优模型，计算特定交通状态、不同大型车占比条件下的全体平均车头时距，体现大型车对通行效率的影响，即

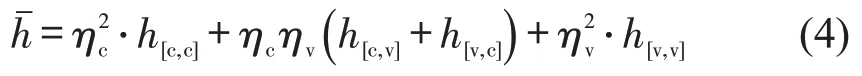
式中：ηc、ηv为目标状态下小型车、大型车占比；h[c,c]、h[c,v]、h[v,c]和h[v,v]对应4 种过车组合在该状态下的拟合车头时距代表参数。

3 实例分析

获取某城市区域内12 处卡口设备及6 处电子警察设备连续7日采集的LPR 数据作为分析基础。该区域流量组成稳定，交叉口设计方案相近，认为同类型LPR数据体现的交通运行特征一致，与设备布设的具体路段或交叉口位置无关，因此，可对同类设备采集的数据合并分析。需要说明的是，选定交叉口LPR 对应的信号相位绿灯时长较接近且均小于80 s，以此为阈值统一对所有交叉口车头时距数据截尾。各集合数据样本量如表1所示。

3.1 车头时距分布模型建模与择优

本次以2～6个密度分支的GMM、LMM以及2～3个密度分支的GLMM拟合表1中各集合的车头时距，即分别对每个集合建立3类13个子模型。考虑EM 算法可能陷入局部最优解的特点，对GMM、LMM 分别进行5 次实验，对GLMM 进行15 次实验，记录多组可能解并保留最优解。为提升效率，每次实验随机从对应集合中无放回抽取3000个样本构成子样本集进行计算。求解后，先以K-S检验所有模型的拟合优度：据样本量，在0.05 显著水平下K-S检验要求经验分布和理论分布最大差值D值为0.0248，对D值超过该阈值的模型予以排除；再对通过检验的模型计算其AIC值，结果如表2所示。

表1 实例应用的分类样本量Table 1 Sample number of each collection

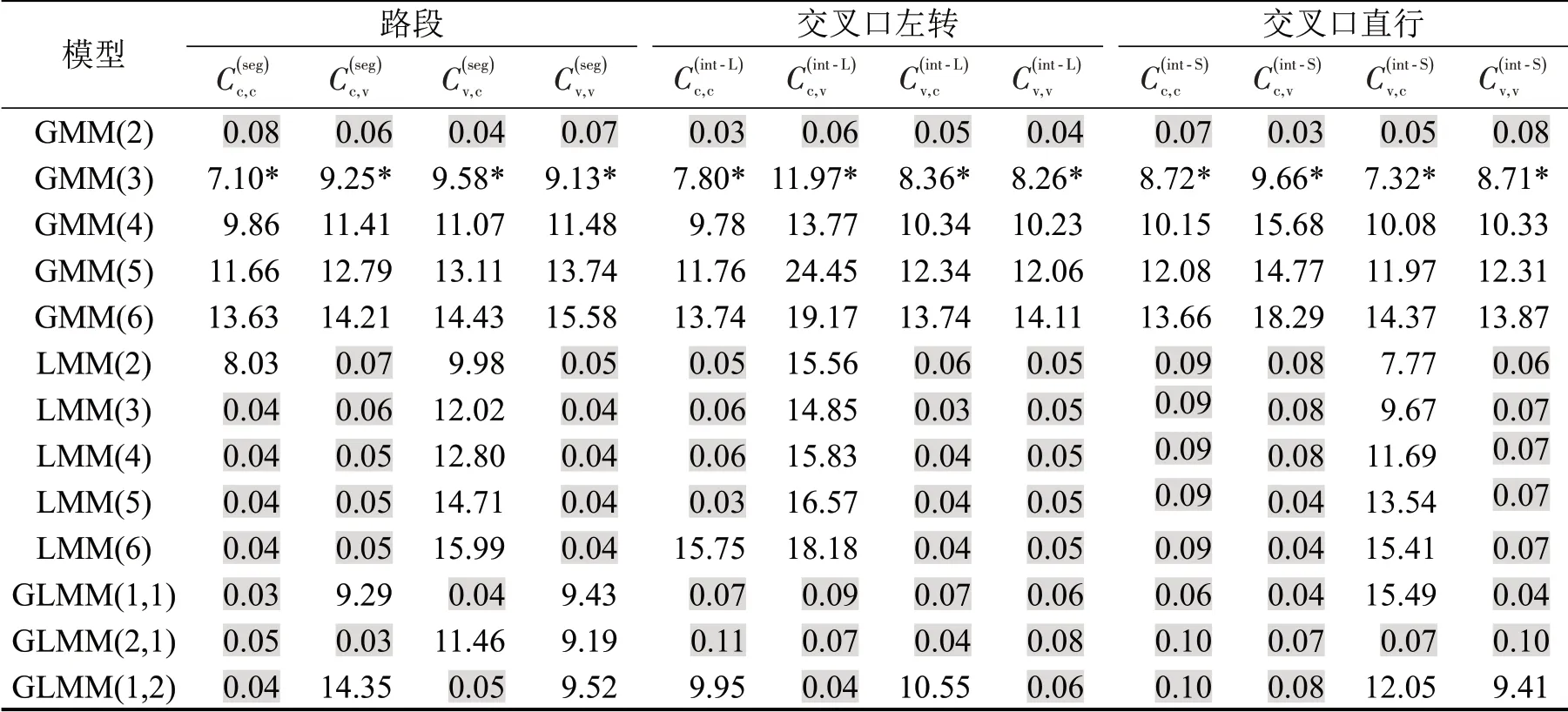
表2 各集合拟合结果的D值或AIC值Table 2 D values or AIC values of models fitting each collection

由表2可知：

(1)因AIC 有高估混合模型分支数的趋势影响[14]，为避免此影响，补充有低估分支数倾向的MDL独立认定最佳模型，结果未改变。

(2)对任意集合，最佳拟合模型均为GMM(3)。据前文分析，不同密度分支对应不同的交通流状态，即各集合中均包括了3种状态下的车头时距分布。其中有最小均值的密度分支(下称“最小均值分支”)代表了车流饱和时的车头时距分布，其参数适用于描述高峰时段的交通流运行情况，是体现大型车对路网运行影响的关键参数。

(3)尽管部分研究以较小样本量验证了单一对数正态模型可描述交叉口直行车道的车头时距分布，但本文基于大量数据和多次检验的结果显示，对数正态分布或LMM并非描述城市路段或交叉口车头时距分布特征的最佳模型，对于多数集合，LMM 甚至无法通过拟合优度检验；通过检验的LMM，其表现也不及相同分支数的GMM。

(4)K-S检验结果显示，高分支数的GMM模型D 值逐渐减小，对于部分集合，拟合与实际的累计频率曲线几乎完全重合。虽然这样的模型对样本拟合能力较好，但AIC 准则判定其并非最优模型，因为AIC同时考察拟合优度及过拟合倾向，而这类模型体现出较强的过拟合倾向，泛化能力较差。这也是GMM和LMM的AIC值一般随分支数的增加而递增的原因。

(6)对于部分集合，GLMM 模型也体现出较好的拟合能力，但其表现稳定性不及GMM。对通过K-S检验的GLMM模型考察，发现其最小均值分支多符合高斯模型，而最大均值分支则多符合对数正态模型，这体现出相对饱和车头时距而言，非饱和车头时距有右偏倾向，即在交通流量较高的城市路网中，非饱和车头时距分布明显向左集中。

(7)考察未通过K-S 检验的LMM 模型，2 个典型示例拟合曲线如图2所示，其中，柱状图为车头时距的频率分布直方图(下同)。

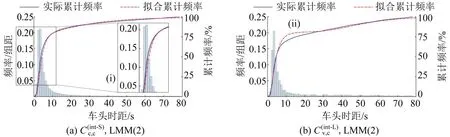
图2 未通过K-S检验的典型LMM模型拟合曲线Fig.2 Cumulative distribution curves of Typical LMMs that fail K-S test

可见，未通过检验的LMM 一般对累计曲线的后半段拟合情况较好，但图2(a)中(i)部分(即放大显示图)和图2(b)中(ii)部分标示出的前半段有较大的D 值，导致模型未通过检验。即使分支数增加，这部分偏差通常也无法得到纠正，故表2中LMM 模型的无效通常是整体性的。这说明分布右偏的模型拟合饱和流车头时距分布的能力较差，不适合作为最小均值密度分支的概率密度函数。

3.2 最优模型特性分析

绘制各集合最佳模型拟合曲线如图3所示。由图3曲线和参数可知：

(1)最佳模型的ωi值可反映样本数据集整体的交通运行情况，最小均值分支对应的ωi越高，说明整体样本中以饱和车头时距连续通过的车辆比重越大。具体到实例数据，路段车头时距的整体饱和程度相对交叉口水平较低，交叉口直行车道连续通过性最好；对于同类过车组合，路段饱和车头时距的σ值也更大，体现其不如交叉口车头时距分布集中的特性。

(2)最大均值分支体现非饱和状态下的交通运行情况，与最小均值分支趋势相反，结果显示交叉口最大均值分支的均值明显大于路段，体现了交叉口信号控制对交通流的阻断作用，使非饱和交通流的车头时距更大、更分散。

(3)最佳模型虽通过了K-S检验，但图3中大部分曲线中段可见最大的D值，说明高斯模型拟合非饱和车头时距能力较弱。综合图2结果，GLMM的优势在于其结合了高斯和正态分布模型对饱和、非饱和交通状态下的描述能力，对部分集合也能产生较好拟合效果。

图3 各集合最佳拟合曲线及参数Fig.3 Best-fit cumulative distribution curve and parameters of each collection

(4)交叉口直行各类过车组合饱和车头时距均值大致相等，非饱和车头时距有差别；而路段、交叉口左转的饱和与非饱和车头时距根据过车组合都有明显差异，即大型车对后两者交通效率影响更大。

(5)各类车道条件下，各类过车组合的车头时距均值有一定规律，无论是否饱和流，通常[c,c]组合的车头时距均值最小，[c,v]和[v,c]组合值较相近，[v,v]组合最大；车头时距分布的σ值有类似变化规律，其中[v,v]组合相对其他3个组合差异水平更大。说明大型车混入车流明显增加了连续流的车间距，并影响车间距的稳定性，对路段和交叉口都产生了不同程度的影响，其中以高峰期间饱和流的大型车影响最为关键。

3.3 基于饱和车头时距的大型车影响分析

示例数据的车头时距混合分布分支均为正态分布，其均值具代表意义。汇总4类过车组合的饱和车头时距均值如表3所示。

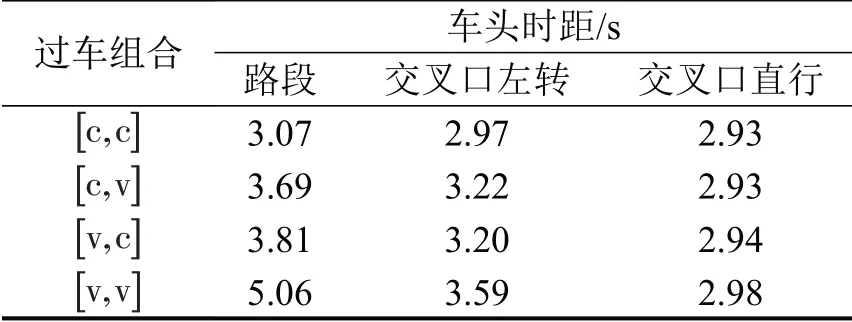
表3 4类过车组合车头时距均值Table 3 Headway averages of 4 types of passing vehicles

根据表3，有以下结论：

(1)交叉口直行饱和车头时距相对路段和交叉口左转更小；左转车流因平顺性和转弯半径等因素影响，车头时距略高于直行，这种差异对[c,c]组合尚不明显，但对后3种组合则较为显著，尤其是[v,v]组合。大型车占比越大，后3种组合出现的频率也越高，对左转车道通行能力的影响越大，对于信控交叉口，意味着有效绿灯时间减少以及交叉口延误增加，是大型车占比上升影响城市道路交通运行效率的微观体现；另外，不同流向车流的车头时距均值差异进一步证明了在研究交叉口车头时距分布时区分流向的必要性。

(2)不同于交叉口因信控影响会集中在绿灯期间放行车队，路段车流多为连续流，其各类过车组合的车头时距均值最大，因此，大型车混入对其通行的影响也更明显，大型车连续通过时，其车头时距相比于小型车连续通过多2 s。

(3)对比[c,c]与[c,v]、[v,c]这3 种组合的车头时距，可见大型车对交通效率的影响同时体现在多个方面：[c,v]与[c,c]对比显示，相比小型车彼此跟随，大型车跟随小型车时倾向于保持更大的车距；[v,c]与[c,c]相比证明，小型车跟随大型车时因大型车车长等因素也有更大的车头时距；对比[v,v]和[v,c]可知，大型车跟随大型车时，其车头时距比小型车跟随大型车有明显增加，这种差别与前车的长度无关，仅由驾驶行为及跟驰车速决策引起，是大型车影响的明显体现。

(4)根据表3，利用式(4)计算大型车占比对全体平均车头时距的影响如图4所示。可见大型车对不同位置的运行效率影响程度有明显差异。

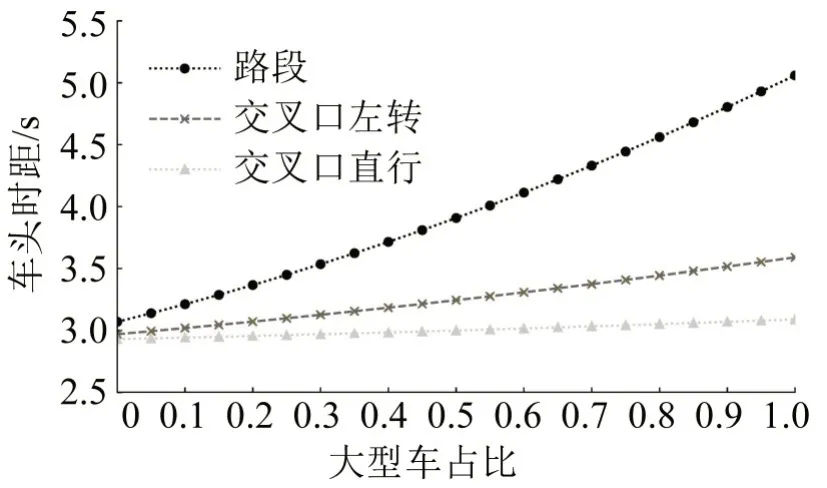
图4 不同大型车占比条件下整体车头时距曲线Fig.4 Headway curves with various large vehicle percentages

4 结论

本文基于LPR数据，建立混合模型研究不同过车组合在不同类型车道的车头时距分布，并分析了大型车对城市交通运行的影响。实例研究表明，以3个密度分支混合的GMM对多场景下各类过车组合车头时距区分建模效果最优，GLMM 模型也体现出局部优势；各模型参数量化了大型车在路段、交叉口直行与左转车流中跟随与被跟随时对交通效率的微观影响，其中交叉口直行车流影响最小，左转次之，路段影响最大；大型车不仅增加了相关过车组合的车头时距均值，更使车头时距稳定性变差，其影响程度可由不同条件下的饱和车头时距对比量化。方法由大量数据驱动，模型细化程度高，可综合反映大型车影响。结合LPR 数据体现的交通组成信息，方法可用于定量评估小型车专用道等管控策略的效用。