基于比功率分布的排放因子速度修正误差控制研究

宋国华，吕海欧，李祖芬，黄健畅

（北京交通大学，综合交通运输大数据应用技术交通运输行业重点实验室，北京 100044）

0 引言

高分辨率的排放因子是通过耦合各平均速度下的机动车比功率(Vehicle Specific Power,VSP)分布和排放率(Emission Rate, ER)得到。目前，交通能耗排放测算对排放因子的精度要求不断提高，本地化数据能提升排放因子的准确性[1]，其中，机动车工况及排放数据的数量与质量是影响准确性的关键因素。一方面，虽然工况数据的采集、储存等成本逐渐降低，但大量的工况数据却未被较好地应用于比功率分布的建立；另一方面，车载尾气检测(Portable Emission Measurement System，PEMS)排放测试的成本远高于工况数据采集成本，且由于特定比功率区间的数据存在数量不足和质量有限的问题，排放率会出现误差。比功率分布和排放率误差耦合导致了排放因子速度修正曲线在平均速度小于80 km·h-1范围内常存在异常波动。曲线异常波动会导致难以准确评估交通管控优化对交通排放的影响。因此，节约成本的同时，如何控制机动车工况和排放数据的数量与质量来降低排放因子速度修正结果误差，得到无异常波动的曲线，成为亟需解决的问题。

既有的排放因子误差研究分为敏感性分析和不确定性分析两类。敏感性分析目的在于识别排放因子结果的影响因素并对其排序，研究方法主要为局部和全局分析方法。局部分析方法由于简单易行，被广泛应用于科学研究，例如，分析机动车排放因子与运行速度[1]、气象参数[2]、车龄[3]、交通状态[4]及道路类型[5]等参数间的关系。相比于局部分析方法，全局分析方法可提供多变量同时变化时的敏感性分析结果，但全局分析方法因计算成本较高，未能有效推广。现有的敏感性分析结果均表明了使用本地化数据的重要性，然而却无法指导本地化数据采集工作。为分析由数据采集造成的排放因子误差，GIECHASKIEL 等[6]估计PEMS 设备采集排放数据的不确定性；张泽禹[7]基于蒙特卡洛模拟，建立了平均速度在20～80 km·h-1内工况和排放数据样本量与排放因子不确定性的关系，但缺乏80～120 km·h-1内工况样本量结果，且排放样本量未细化至比功率区间，无法精细化指导数据采集工作。

综上所述，既有研究虽然指出了排放因子的部分影响因素，但仍存在不足：缺乏比功率分布和排放率对排放因子速度修正结果的影响机理研究；关于排放因子曲线在某些速度区间异常波动的讨论较少；未计算高速区间机动车工况数据需求量，排放数据需求量的计算结果未细化至比功率区间。

因此，为提高排放因子速度修正结果准确性，本文基于实测数据建立排放因子速度修正曲线并开展影响机理研究，从比功率分布和排放率两个角度，分析特定误差下的排放因子敏感性、区间容许误差，建立机动车工况数据和PEMS排放数据需求量模型，为本地化数据采集工作提供参考，有效克服曲线异常波动问题，提高排放因子可靠性，为节能减排工作提供支持。

1 无异常波动的排放因子速度修正曲线建立方法

排放因子是机动车行驶单位距离所排放污染物的质量(g·km-1)，特定平均速度下高分辨率的排放因子计算方法为

式中：k为平均速度(km·h-1)；为平均速度k的排放因子(g·km-1)；为第i个比功率区间的排放率(g·s-1)；为平均速度为k时第i个比功率区间的分布值，无量纲。

特定平均速度下代表性的快速路比功率分布的建立，可通过采集机动车逐秒工况数据，筛选出60 s 连续数据构成1 组行驶轨迹数据[8]。但实际工况中，采集的逐秒工况数据难以被证明可得到精准的排放因子速度修正曲线。为得到无异常波动排放因子速度修正曲线作为研究基础，基于比功率分布严格服从正态分布[9]，以比功率聚类单位为步长积分得到比功率分布，定义各平均速度下比功率分布概率密度函数为

式中：VVSP为比功率值(kW·t-1)；μ为均值(kW·t-1)；σ为标准差。

现有排放数据表明：当比功率小于0 kW·t-1时，CO2排放率基本保持稳定；当比功率大于0 kW·t-1时，CO2排放率与比功率具有相对良好的线性关系[8]，如图1所示。因此，可通过建立线性模型得到特定比功率区间的CO2排放率。耦合各平均速度下的正态比功率分布和线性排放率，即可得到无异常波动的排放因子速度修正曲线。

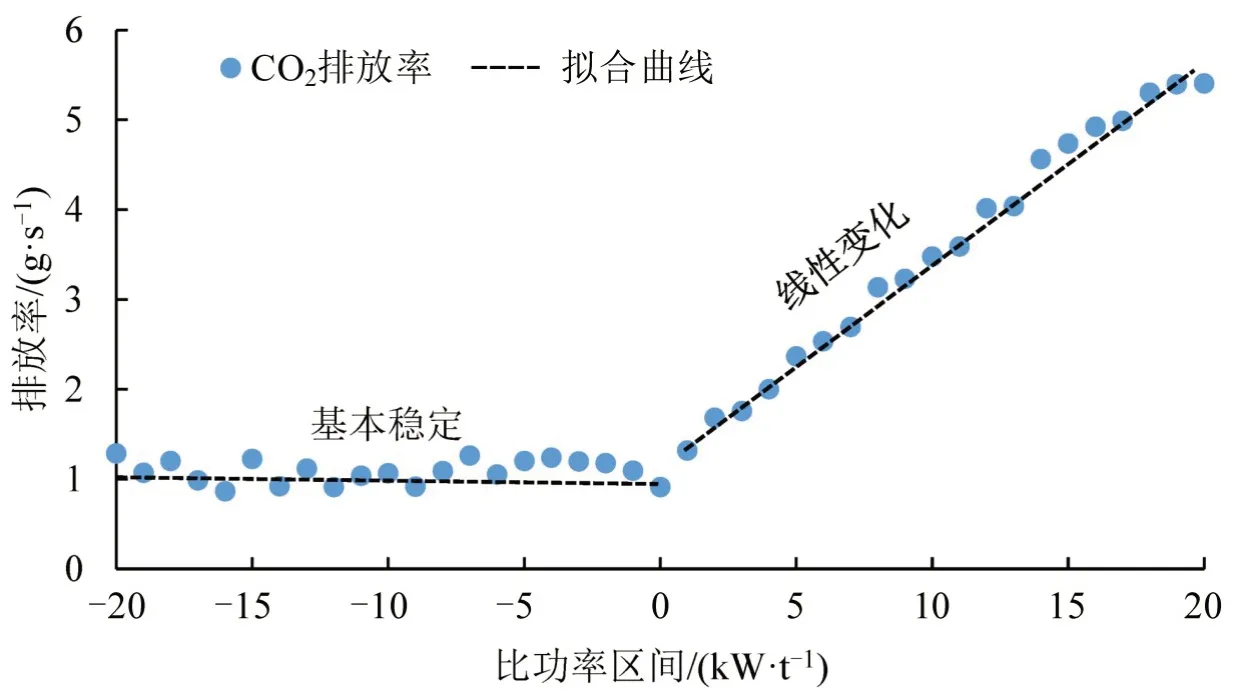
图1 轻型车CO2排放率Fig.1 CO2 emission rates for light-duty vehicles

2 模型的建立

首先，分别从比功率分布和排放率两个角度定量刻画排放因子敏感性。其次，基于各区间敏感性的差异，分析限定误差下特定速度-比功率区间分布值的容许误差和特定比功率区间排放率的容许误差。最后，基于敏感性分析和容许误差结果，分别建立限定排放因子误差前提下的机动车工况数据和PEMS排放数据需求量模型。技术路线如图2所示。

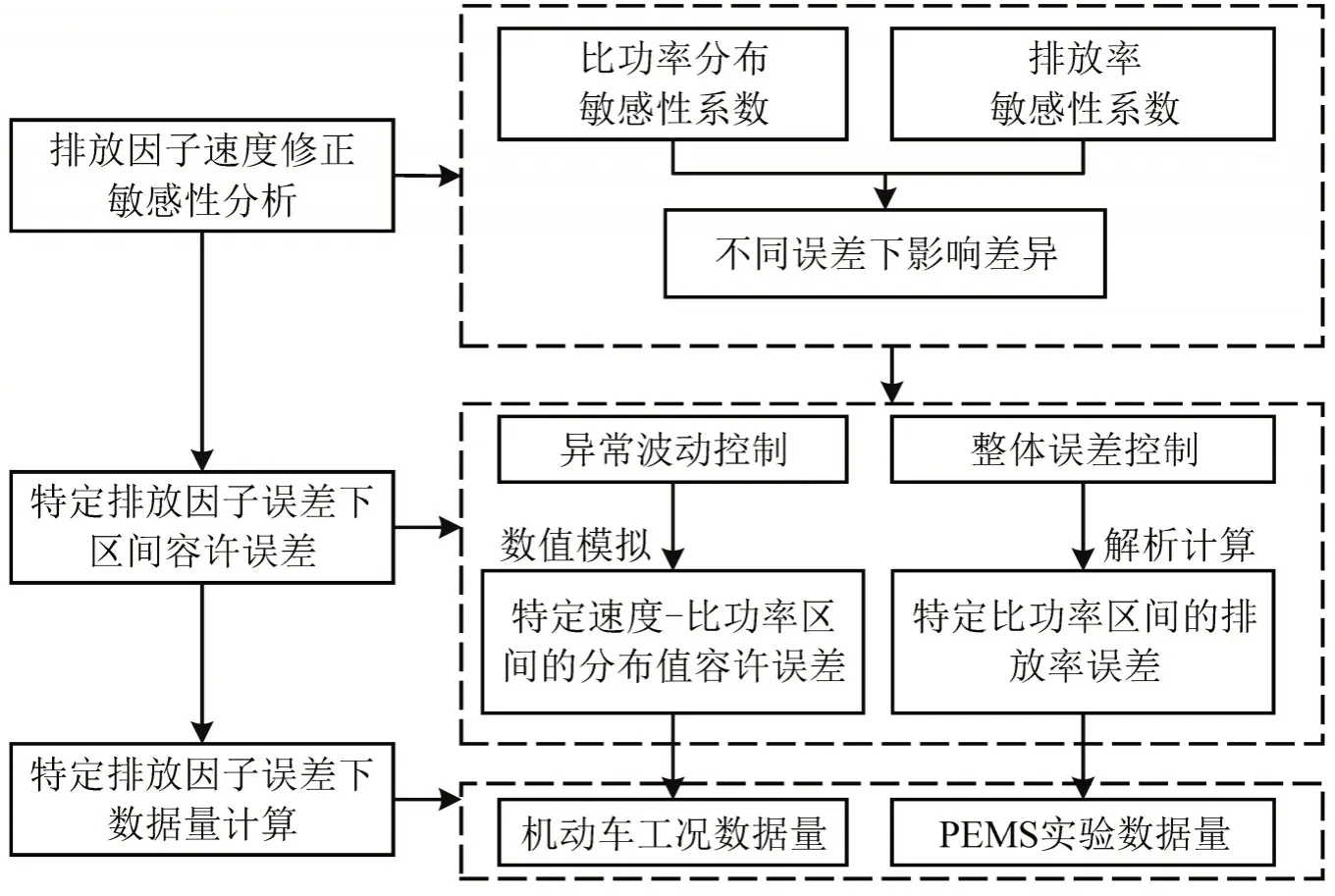
图2 技术路线Fig.2 Design of study

2.1 排放因子速度修正敏感性分析

由于局部分析法中的单变量法计算量小、便于应用，因此，采用该方法进行敏感性分析，分别建立排放因子对比功率分布和排放率的敏感性系数，即

式中：、分别为平均速度k下第i个比功率区间的比功率分布和排放率敏感性系数；为平均速度k下排放因子变动值；为平均速度k下第i个比功率区间分布值变化量；为第i个比功率区间排放率变化量。A(k,i)大于0表示排放因子与变量同向变化，A(k,i)越大表明排放因子对变量变化越敏感。

2.2 比功率分布和排放率区间容许误差分析

在限定排放因子速度修正误差的基础上，设定比功率区间分布值的变动单位，遍历所有比功率区间，排放因子误差等于限定值，分布值变化量即为当前区间的容许误差，即

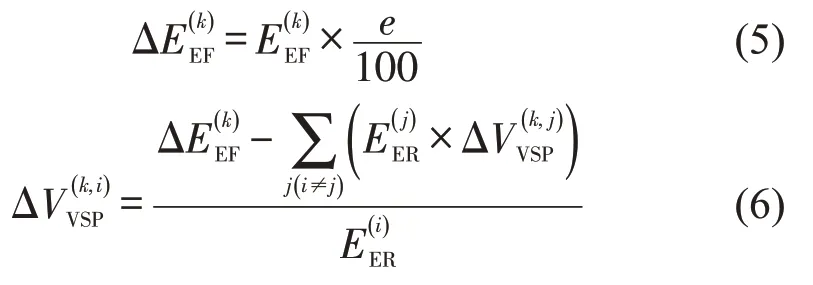
同理，在限定误差的基础上，可得排放率理论容许误差为

考虑各比功率区间排放率的容许误差应不大于排放率值，设定排放率容许误差约束为

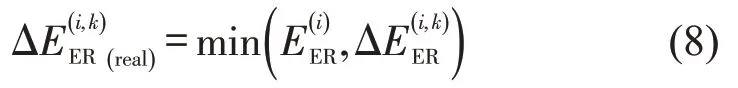
2.3 机动车工况数据和PEMS 排放数据需求量模型

基于特定速度下比功率分布的正态性和容许误差，建立特定排放因子速度修正误差下各平均速度的工况数据需求量计算式为

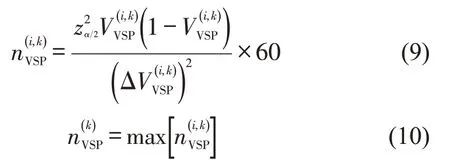
式中：为平均速度k下第i个比功率区间的工况数据需求量(s)；α为显著性水平，本文中为0.05；zα2为1-α置信水平下的Z 统计量；为特定排放因子速度修正误差和置信水平下，平均速度k下工况数据需求量(s)。

利用特定比功率区间排放率数据的正态性[8]和实际容许误差，建立PEMS 排放数据需求量计算式为

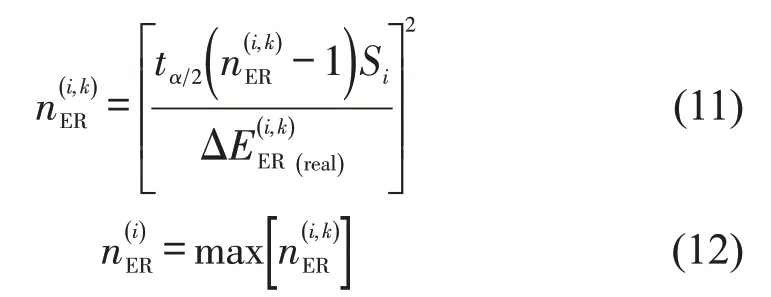
3 数值模拟计算

定量分析问题通常可用解析法或数值模拟法解决。解析法适用于变量间关系简单、易于求解的情况；数值法常用于需要全域数据而实验只能采集到个别情况的数据，或模型仅能求出在离散点处数值解的情况。本文基于实测数据建立离散的排放率和比功率分布，为克服实测数据的随机性，采用数值模拟方法建立各种情况下的排放率和比功率分布，计算出两者的敏感性系数和容许误差；而工况数据和排放数据需求量则结合统计学理论，由解析法求解。因此，本文采用数值模拟和解析计算相结合的方法开展研究。

3.1 参数设定

比功率聚类单位间隔越小，排放计算越精确。在北京市道路运行状况下，比功率绝对值小于20 kW·t-1的样本约占总样本的98%。研究设定比功率聚类单位间隔为1 kW·t-1，覆盖区间范围为[-20，20] kW·t-1。据此，利用平均速度在20～120 km·h-1内的北京市快速路轻型车2017年5月21日的31892709 条逐秒行驶工况数据，根据文献[9]，建立比功率分布概率密度函数，以1 kW·t-1为步长积分得到比功率分布，即

式中：k为平均速度(km·h-1)；f(VVSP)为比功率分布概率密度函数。

利用北京市3 辆轻型车2009年5月8日的10870 条PEMS 排放数据及速度信息，建立CO2排放率公式为

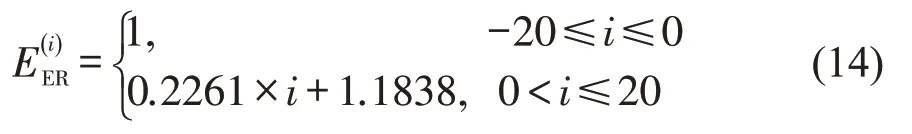
式中：i为第i个比功率区间，取值为整数。

耦合得到无异常波动排放因子速度修正曲线。考虑比功率分布值降低和增加两种情况确定其容许误差。基于分布值数量级和计算机性能，设定变动单位为0.01%。为保证比功率分布值各区间总和为1，增加(或降低)某区间分布值的同时，按比例降低(或增加)其余各区间分布值。排放率容许误差由式(8)可得。

3.2 排放因子速度修正敏感性分析结果

各比功率区间的敏感性存在差异，随平均速度增大，敏感性系数最大值逐渐降低，敏感区间分布更加分散。例如，平均速度为40 km·h-1，最大系数出现在0 kW·t-1，为0.04。排放因子对各比功率区间分布值的敏感性系数如图3所示。

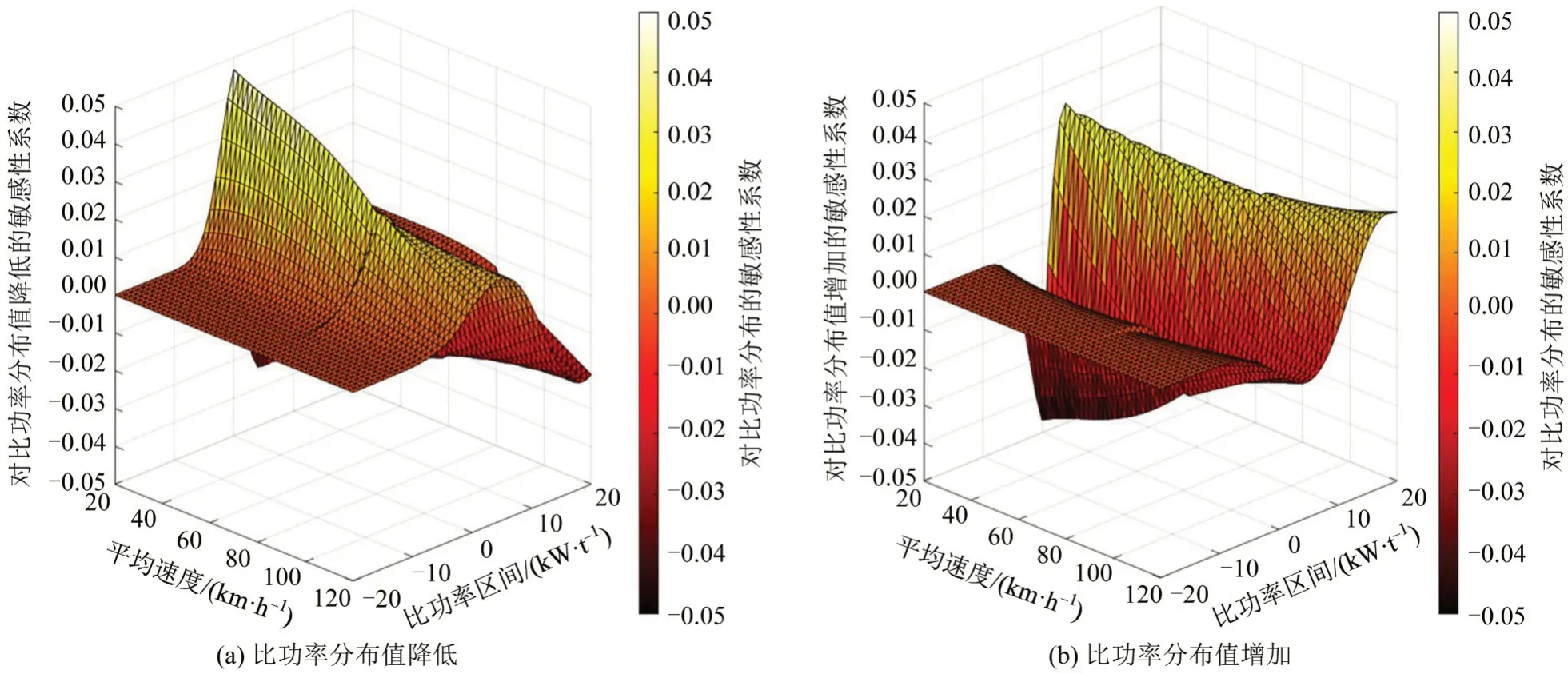
图3 排放因子对各比功率区间分布值的敏感性系数Fig.3 Sensitivity coefficient of emission factor to distribution of each VSPBin

以耦合得到的无异常波动曲线为基准曲线，建立不同比功率分布误差下CO2排放因子速度修正曲线，如图4所示。例如，比功率误差区间为0 kW·t-1，比功率分布误差为5%，即平均速度为40 km·h-1时，比功率区间0的分布值增加5%，其余同理。

由图4可知，不同比功率区间对排放因子的影响不同，排放因子误差与比功率分布误差成正比；比功率分布误差是导致排放因子速度修正曲线产生异常波动的重要原因。因此，控制比功率分布误差，可避免排放因子速度修正曲线产生异常波动。

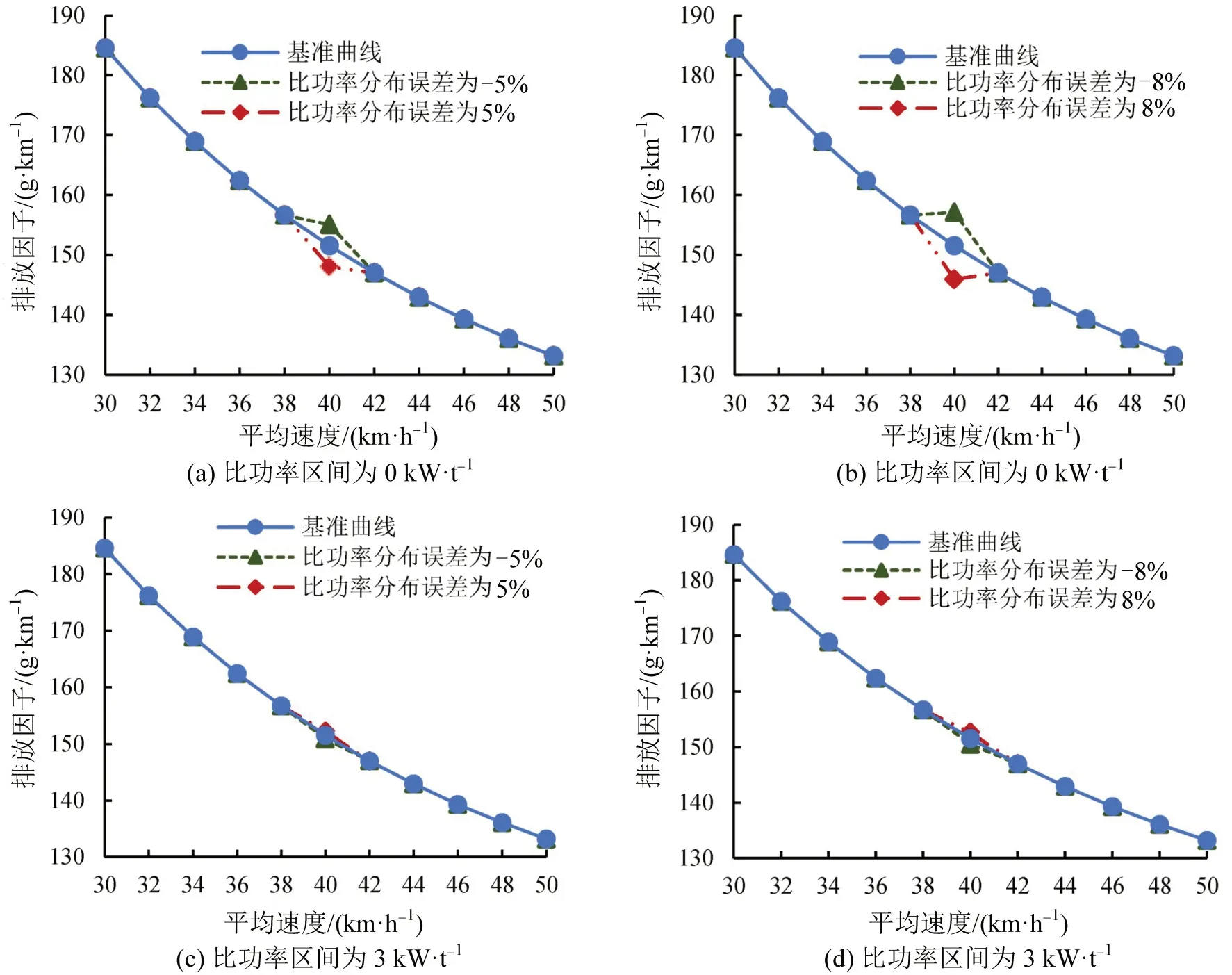
图4 不同比功率分布误差情况下CO2排放因子速度修正曲线Fig.4 CO2 emission factor speed correction curves under different VSP distribution errors

排放因子对各比功率区间排放率的敏感性系数，受特定平均速度下比功率分布变化趋势影响，敏感性较大的排放率区间随速度的增大逐渐右移，最大敏感性系数逐渐减小。平均速度为40 km·h-1时，最大系数出现在4 kW·t-1，为0.11。排放因子对比功率区间排放率的敏感性如图5所示。

图5 排放因子对各比功率区间排放率的敏感性系数Fig.5 Sensitivity coefficient of emission factor to emission rate of each VSPBin

建立不同排放率误差下的排放因子速度修正曲线，如图6所示。例如，比功率区间为0 kW·t-1，排放率误差为-10%，即比功率区间0的排放率降低10%，其余同理。

由图6可知，不同区间排放率对于排放因子的影响不同，排放因子误差与排放率误差成正比；排放率对排放因子速度修正结果的影响是整体的，通过控制排放率误差，可降低排放因子曲线整体误差。

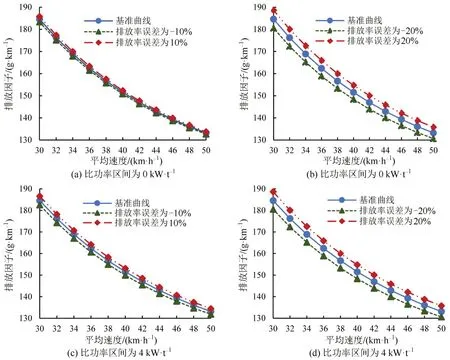
图6 不同比功率区间排放率误差下的CO2排放因子速度修正曲线Fig.6 CO2 emission factor speed correction curves under different emission rate errors in different VSP Bins

3.3 比功率分布和排放率区间容许误差分析结果

控制排放率不变，平均速度在20～120 km·h-1内排放因子误差不超过5%、3%和1%，各比功率区间分布值在降低时的容许误差如图7所示。

控制排放率不变，平均速度在20～120 km·h-1内排放因子误差不超过5%、3%和1%，各比功率区间分布值在增加时的容许误差如图8所示。

由图7和图8可知：各区间分布值容许误差与排放因子误差成正比；排放因子误差为定值时，容许误差较大的比功率区间随平均速度增加逐渐右移，最大容许误差逐渐减小；部分比功率区间分布值降至0 kW·t-1，排放因子误差仍未超限。提高上述区间分布值的准确性，对降低排放因子误差意义较小。因此，在确定工况数据量时不考虑该部分区间。

在排放因子误差不超过1%的基础上，控制曲线在平均速度小于80 km·h-1内无异常波动，得到平均速度为76 km·h-1时分布值容许误差，如图9所示。相比于图7和图8，图9中各比功率区间分布值容许误差显著降低。

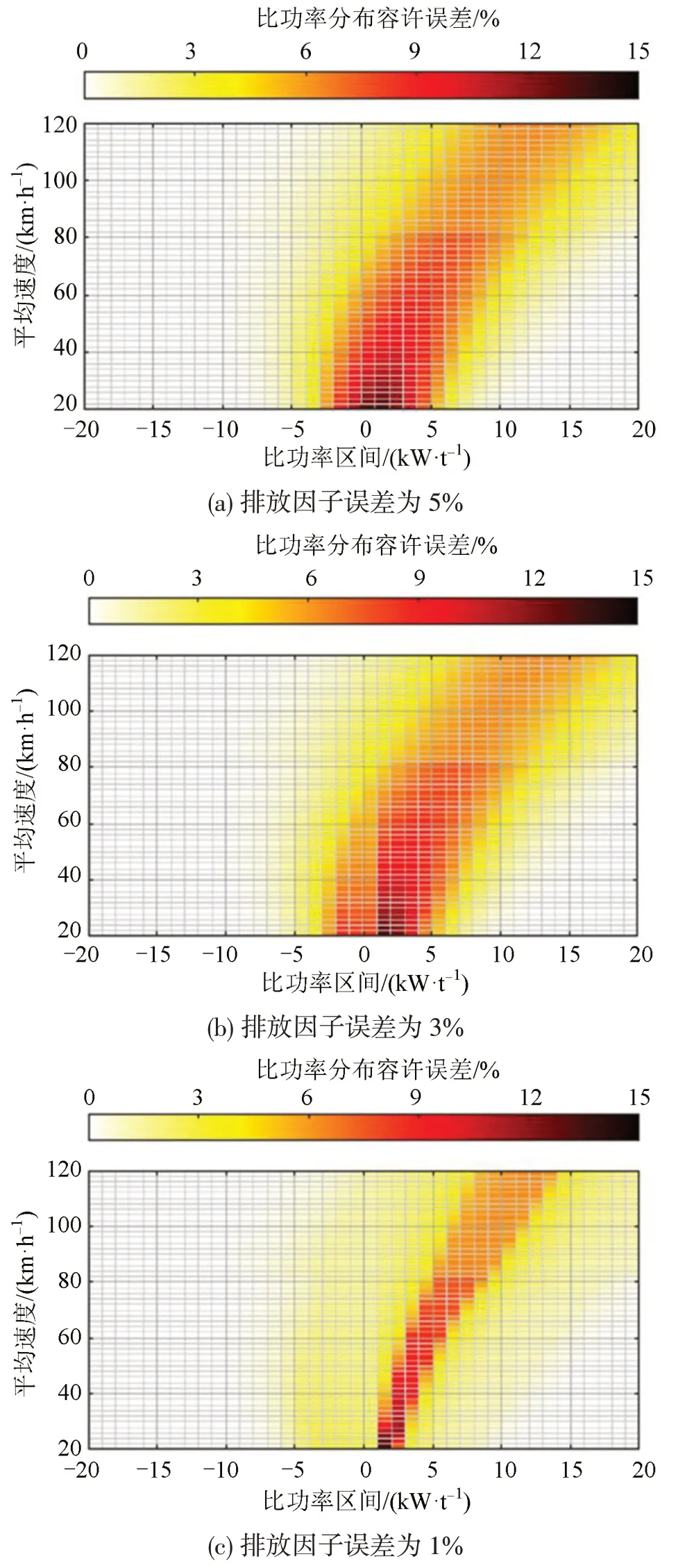
图7 比功率分布值降低时的容许误差Fig.7 Allowable errors of VSP distribution under condition of decreasing

图8 比功率分布值增加时的容许误差Fig.8 Allowable errors of VSP distribution under condition of increasing

图9 平均速度为76 km·h-1时各比功率区间分布值容许误差Fig.9 Allowable errors of VSP distribution under speed of 76 km·h-1

控制比功率分布不变，平均速度在20～120 km·h-1内排放因子误差均不超过1%，建立CO2排放率容许误差如图10所示。由图10可知，排放因子误差为定值时，特定平均速度下排放率容许误差随比功率增大先降低后增加；比功率大于0 时，排放率容许误差随速度增大而降低。

图10 CO2排放因子速度修正误差为1%时排放率容许误差Fig.10 Allowable errors of emission rates under CO2 emission factors speed correction errors of 1%

3.4 机动车工况数据和PEMS 排放数据需求量计算

排放因子误差不超过1%时，各平均速度下的工况数据需求量如图11所示。由图11可知，工况数据需求量随平均速度先增大后减小，在平均速度大于100 km·h-1后，需求量又呈现逐渐增大的趋势。在95%的置信水平下，控制排放因子误差均不超过5%、3%和1%，分别需要30，85，710 min 的工况数据，数据需求量与误差比值的平方成正比。

满足排放因子误差均不超过1%，且曲线在平均速度小于80 km·h-1内无异常波动，所需机动车工况数据量如表1所示。

由图11和表1可知，平均速度小于64 km·h-1时，满足误差不超过1%，即可保证曲线在该范围内无异常波动。平均速度在64～80 km·h-1之间时，容许误差较小，增加该部分工况数据量，可避免曲线在64～80 km·h-1范围内产生异常波动。

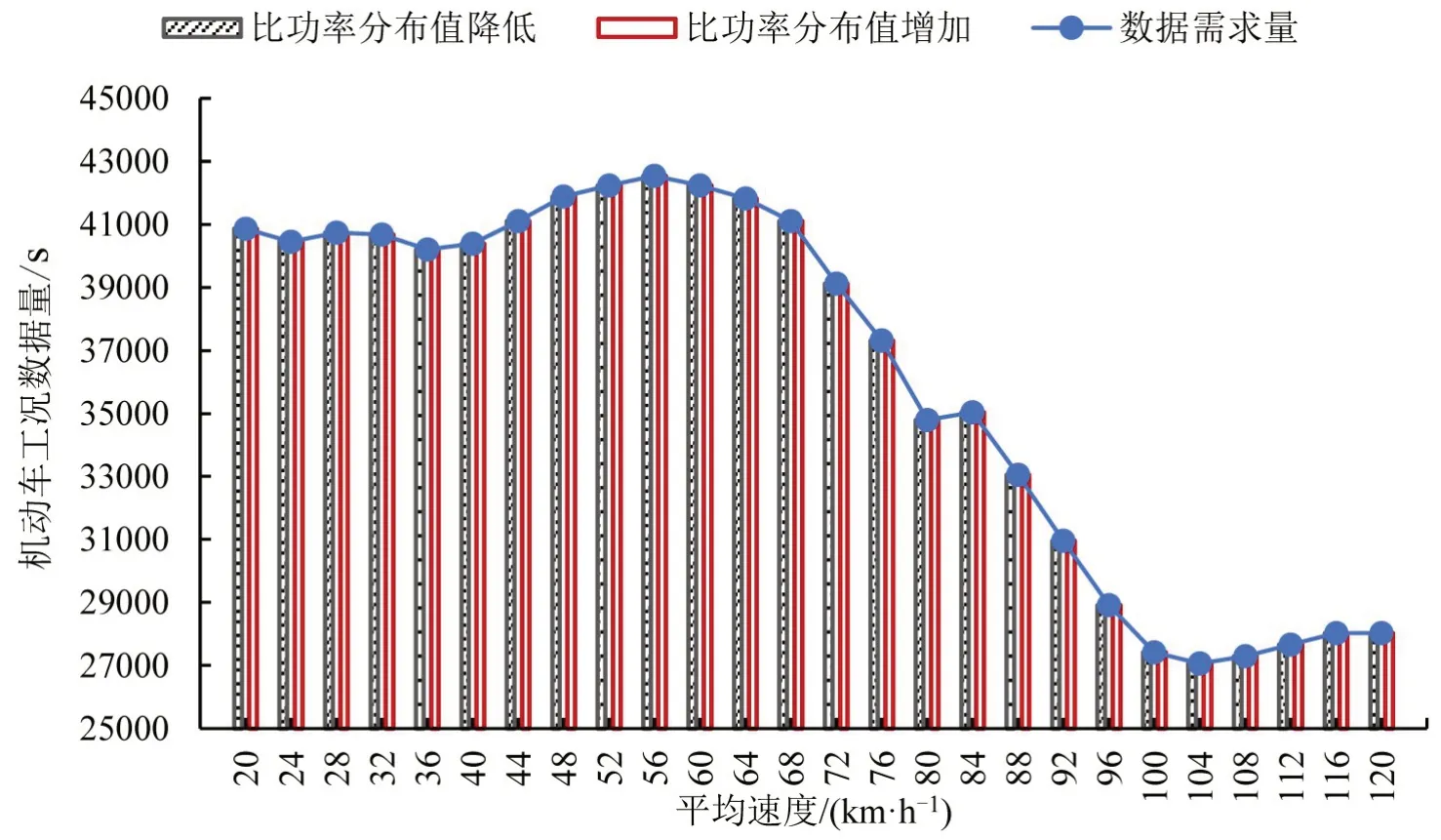
图11 CO2排放因子速度修正误差为1%时机动车工况数据量Fig.11 Number of vehicle operation data under CO2 emission factors speed correction errors of 1%

采用2012年9月北京市快速路轻型车的2421630 条工况数据进行验证。根据3%误差时特定速度下的工况数据需求量，在各平均速度下随机抽取数据，重复抽取50次，得到样本与总体结果的相对误差，如图12所示。

由图12可知，各平均速度下误差的95%置信上限均小于等于3%，验证得到本文提出的数据需求量可以满足排放因子速度修正误差控制需求。现实中，数据采集受多因素影响，质量无法保证，部分平均速度下的数据量不足，表1结果可用于指导机动车工况数据的采集工作，避免由于比功率分布误差引起曲线异常波动。

图12 排放因子速度修正结果相对误差Fig.12 Relative errors of emission factors speed correction

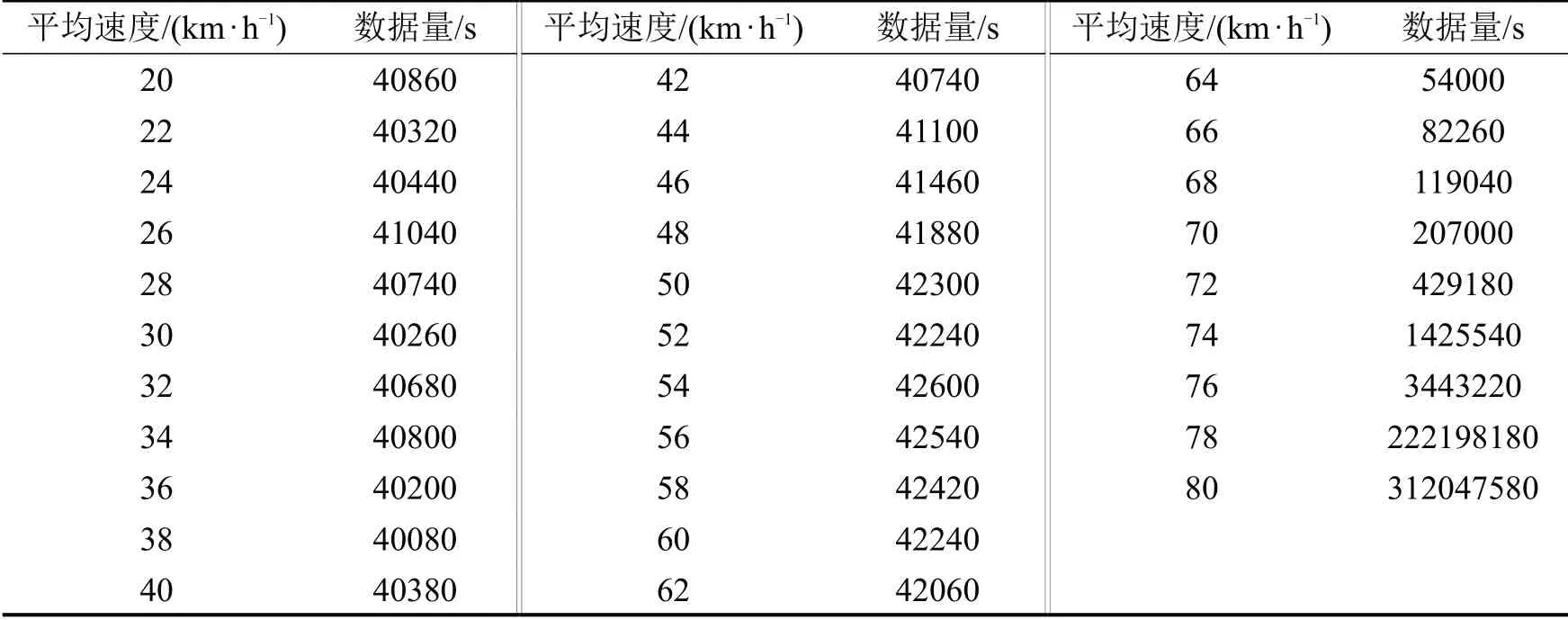
表1 CO2排放因子速度修正曲线无异常波动时机动车工况数据需求量Table 1 Number of vehicle operation data under CO2 emission factors speed correction curve no abnormal fluctuation

在95%的置信水平下，满足排放因子误差不超过1%，各比功率区间排放数据需求量如表2所示。考虑统计学意义，表2已将结果中不足3 s的替换为3 s。

由表2可知，[-20,-9]比功率区间原始结果均不足3 s。这是由于这些区间分布值较低，排放因子对其排放率变化不敏感。在95%的置信水平下，控制排放因子误差不超过1%，需40 min 的排放数据，其中[-3, 9]区间数据需求量占总需求量的83.6%。

采用北京市2015年3月11日的8140条轻型车排放数据和表2中各比功率区间的数据需求量，在各比功率区间随机抽取数据，重复抽取50次，得到样本与总体结果的相对误差，如图13所示。

由图13可知，各平均速度下误差的95%置信上限均小于等于1%，验证得到本文提出的数据需求量可以满足排放因子速度修正误差控制需求。利用PEMS采集排放数据时，可参考表2结果，以保证各个比功率区间采集到相对可靠的排放数据，从而控制排放因子速度修正误差在特定范围内。

表2 CO2排放因子速度修正误差为1%时PEMS排放数据需求量Table 2 Number of PEMS emission data under CO2 emission factors speed correction errors of 1%

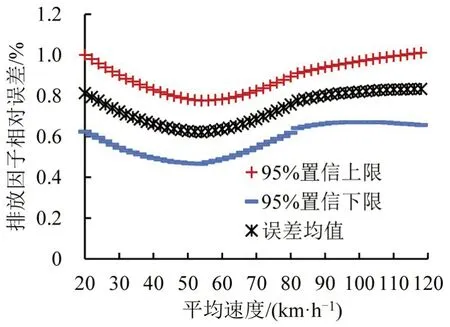
图13 排放因子速度修正结果相对误差Fig.13 Relative errors of emission factors speed correction

4 结论

针对排放因子速度修正曲线常存在异常波动问题，本文从比功率分布和排放率两个角度出发，揭示对排放因子速度修正结果的影响机理，得到曲线异常波动的产生原因，建立特定排放因子误差下的数据需求量模型，得到以下结论。

(1)通过分析排放因子对比功率分布和排放率的敏感性，发现两者影响机理差异明显：比功率分布误差是造成排放因子速度修正曲线产生异常波动的重要原因；而排放率误差则会导致排放因子速度修正结果出现整体性误差。

(2)基于曲线异常波动的产生原因，在限定排放因子速度修正误差的基础上，通过数值模拟得到所有区间的容许误差及数据需求量。结果表明，为避免排放因子速度修正曲线出现异常波动，平均速度64～80 km·h-1内需采集的工况数据量显著高于20～64 km·h-1内。

(3)在95%的置信水平下，当平均速度在20～120 km·h-1内，限制快速路轻型车CO2排放因子速度修正误差不超过5%、3%和1%，在特定平均速度下分别需采集30，85，710 min的工况数据。相同误差下，80～120 km·h-1内工况数据需求量更低。限制排放因子误差不超过1%，得到细化至1 kW·t-1粒度的各比功率区间PEMS排放数据需求量，各比功率区间的排放数据需求量差异显著，[-3,9]比功率区间的需求量最大。