联合改进STA/LTA与MLoG算子的微震P波到时自动拾取方法

王议迎，丁仁伟,2，3，李建平,4，赵俐红,2，3，赵 硕，张硕伟

(1. 山东科技大学 地球科学与工程学院，山东 青岛 266590; 2. 青岛海洋科学与技术国家实验室，山东 青岛 266237; 3. 海洋矿产资源评价与探测技术国家功能实验室，山东 青岛 266237;4. 山东省物化探勘查院，山东 济南 221116)

微地震监测已经成为当今油藏地球物理描述和二氧化碳地质储存检测等方面的关键技术手段[1]。在非常规油气开采过程中，为了提高油气产量,在储层附近进行高压注液，从而产生微裂缝、诱发微地震。实时绘制微震震源，能更好地控制注入过程从而提高储层开发的效率[2]。因此，微震的自动检测对于监测诱导水力压裂过程至关重要。

随着微震记录数据规模的增大，手动拾取微震到时变得更具挑战性和不可靠，且可能会产生若干假警报或出现到时误拾现象。因此，各种自动或半自动的方法被提出并广泛用于微地震震相拾取。现有的微震震相自动拾取方法主要有长短时窗平均能量比法(short-term average/long-term average, STA/LTA)[3]，该算法简单、计算效率高、适于实时处理。在过去的几十年里，许多研究人员对该方法进行了改进，通过构建不同的特征函数或构建能反映信号振幅强度与频率变化的权值函数等方式获取更准确的微震到时拾取结果[4-10]。自回归(auto regressive, AR)是另一种常用的到时自动拾取方法[11]，该方法基于统计特性的差异将微震记录分为真实微震信号到达前和到达后两个部分，用以表征微震记录。在此基础上，Akaike[12]提出了Akaike信息准则(Akaike information criterion, AIC)方法，将微震数据建模为AR过程，将AIC最小值设定为微震事件的起始时间。除此之外，高阶统计法[13]、神经网络方法[14]、相关法[15]以及偏振分析方法[16]等也被广泛应用于微震震相到时拾取。然而，这些方法需要提前得知检测间隔、人为设置阈值，并需要根据信号强度或时间域特征、频率域特征、综合特征等不断调整拾取参数，降低了方法的普适性。

对于低信噪比的微震数据，微震记录信号中包含大量随机噪声，这对微震震相的到时拾取是一项极大的挑战。为了去除随机噪声对拾取震相到时准确性的影响，常用噪声压制的方法来提高原始数据的信噪比。Chen等[17]提出基于f-x经验模态分解的预测滤波方法，克服了传统f-x预测滤波处理多倾角微震剖面的局限性。Han等[18]提出一种结合自适应阈值的集成经验模态分解(ensemble empirical mode decomposition, EEMD)微地震降噪方法，通过解决模态混合问题改进了经验模态分解(empirical mode decomposition, EMD)，能够更好地将包含噪声的微震数据分解为噪声和有效信号两部分。Huang等[19]提出数学形态学滤波(mathematical morphology filter, MMF)方法，在抑制低频噪声的同时保留信号的低频成分。Li等[20]提出一种数学形态学理论，通过区分微震信号与背景噪声来抑制低频噪声。这些滤波方法虽取得了较好的降噪效果，但在强随机噪声干扰下未能保留微震数据的有效信号形态。

高斯拉普拉斯(Laplacian of Gaussian, LoG)算子源于Marr和Hildreth[21]提出的视觉理论，自提出后就受到了广泛关注。在图像处理领域，LoG算子滤波器被广泛应用于边缘检测等众多图像处理领域。Saad等[22]提出改进的高斯拉普拉斯(modified Laplacian of Gaussian, MLoG)算子滤波方法，利用高斯平滑滤波器和拉普拉斯锐化滤波器，通过平滑背景噪声来检测微震信号的突变。为准确拾取微震P波到时，本研究利用MLoG算子滤波方法提高微震数据的信噪比，然后通过新提出的特征函数，在滑动时窗内分别计算STA和LTA的值，绘制STA/LTA曲线，曲线的峰值记为微震P波到时。

1 改进的STA/LTA方法

STA/LTA最早由Stevenson[3]用于拾取微震震相到时，通过STA与LTA之比反映微震信号振幅和能量的变化。STA主要反映微震信号能量的平均值，LTA主要反映背景噪声能量的平均值。当微震信号到达时，STA比LTA变化快，相应的STA/LTA值会出现明显的增加，当某一时刻其比值大于预先设定的触发阈值时，即可判定该时刻为P波的到时，从而达到自动检测和拾取P波到时的目的。STA/LTA方法计算公式为[6]：

(1)

式中：STAi和LTAi(i=1，2，…，N)分别为微震信号在i时刻的短时窗平均能量值和长时窗平均能量值；NSTA和NLTA分别为对应的短时窗长度和长时窗长度；CFj(j=1，2，…，M)为信号在j时刻的特征函数值，表征微震数据的振幅、频率与能量的变化情况。

STA/LTA方法基于特征函数的突变进行识别。不同特征函数对信号变化的灵敏度不同，具有不同的识别能力。选取适当的特征函数对准确拾取微震到时极为重要，常用的特征函数有[7-8]：

CF1=|X(i)|，

(2)

(3)

(4)

式中X(i)代表原始微震事件在第i个采样点的输入信号。特征函数CF1和CF2仅对振幅变化响应；特征函数CF3对振幅变化和频率变化都有响应。刘晗等[9]指出特征函数CF2和CF3的检测效果较好，但极易受到噪声的干扰，对微震P波到时的自动拾取带来一定误差，从而影响拾取结果的准确性。

(3)纸浆洗涤过程t时刻的操作参数为q(t)=[q1(t), q2(t), q3(t)]。其中，q1(t)为上浆浓度，q2(t)为上浆流量，q3(t)为清水加入量。

为了增强算法对振幅和频率变化的敏感度，Allen[4]、刘晓明等[8]对传统STA/LTA方法进行了改进并用来进行微震事件的检测和震相到时拾取。

Allen[4]改进的特征函数为：

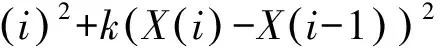
(5)

其中：X(i)为原始微震事件在第i个采样点的输入信号；k为权重因子，是根据输入信号X(i)的采样频率和噪声特性，对信号振幅和频率的权重进行分配：

(6)

刘晓明等[8]在公式(5)的基础上进行改进，计算整个微震事件序列X(i)的权值。改进后的公式为：

(7)

其中，

(8)

文献[4，8]根据输入信号X(i)的采样频率和噪声特性，引入权重因子k对信号振幅和频率的权重进行分配，构建了一种新的特征函数，克服了传统方法不能适应复杂多变的微震信号到时拾取的缺点。然而，这些方法在低信噪比的微震数据应用中，由于输入信号X(i)受到噪声的影响较大，往往得不到准确的到时结果。

本方法根据信号包含的能量、振幅、频率变化等特性，结合特征函数CF2，增强真实信号与噪声的信噪比，以微震时间序列的振幅平方X(i)2，即特征函数CF2作为输入信号。鉴于Allen[4]、刘晓明等[8]的权值构建思想，构建了一种新的特征函数：

(9)

压裂进行时，施工噪音较大，压裂产生的微地震事件通常被强的背景噪声淹没，远高于系统分辨微地震事件的水平，且难以从记录波形中被人工识别出来[10]。因此，针对低信噪比的微震数据，在应用STA/LTA算法前，使用Saad等[22]提出的MLoG滤波方法去除背景噪声，用来提高微震数据的信噪比。MLoG算子滤波方法的表达式为：

(10)

式中：σ为高斯滤波器的标准偏差，n为高斯指数，C为滤波阶数。

通过MLoG算子滤波器对背景噪声进行平滑处理，增强了微震数据细节；在保留原始数据特征的基础上进行去噪，使微震有效信号与背景噪声之间的差值最大化，增强信噪比。利用本方法进行微震P波到时拾取的基本流程如图1所示。

图1 微震P波到时拾取流程图

2 模型验证

本节首先通过模拟数据来验证改进的STA/LTA算法的自动拾取效果。模拟数据的采样频率设置为1 000 Hz，信噪比设置为20，选取的采样点数为3 500。

图2(a)为模拟微震数据记录。对该数据分别采用特征函数CF2和CF4得到的STA/LTA进行到时拾取，对应的长时窗NLTA设置为50 ms，短时窗NSTA设置为20 ms。图2(b)为图2(a)模拟微震数据的特征函数CF2和CF4响应结果；图2(c)为对图2(a)分别利用特征函数CF2和CF4进行计算的STA/LTA到时拾取结果。可以看出，基于两种特征函数的STA/LTA拾取的P波到时与模拟的数据记录完全对应，证明了改进的特征函数CF4理论正确并且可行。

为验证算法在弱信噪比情况下微震事件的识别能力，对图2(a)中的模拟微震数据记录添加了90 dB高斯白噪声，见图3(a)。图3(b)为特征函数CF2和CF4对加噪后微震数据的响应结果。图3(c)为对应的STA/LTA到时拾取结果。可以看出，在90 dB噪声干扰下，特征函数CF4对应的STA/LTA曲线在微震有效信号到来时刻的幅值变化更加明显，对应的P波到时与利用CF2得到的STA/LTA拾取结果一致，表明基于特征函数CF4的STA/LTA的微震到时拾取方法具有一定的抗噪性和准确性。

为进一步验证算法的抗噪声干扰能力，对图2(a)中的合成数据记录添加100 dB高斯白噪声，见图4(a)。图4(b)为直接采用特征函数CF2和CF4对添加100 dB高斯白噪声合成数据的响应结果。对该合成数据采用特征函数CF2和CF4的STA/LTA进行到时拾取时，无法准确拾取P波到时，见图4(c)。造成这一现象的原因是噪声干扰强度太大，真实的微震信号被强噪声淹没。因此，为了有效解决这一问题，利用MLoG低通滤波方法对图4(a)中的微震数据进行滤波处理，相应的参数σ为10,n为32，滤波结果见图5(a)。与图2(a)相比，MLoG滤波后的微震数据虽然降低了微震能量幅值，但有效保留了原始信号形态特征。图5(b)为特征函数CF2和CF4对图4(a)滤波后微震数据的响应结果。图5(c)为滤波后微震数据CF2和CF4的STA/LTA的到时拾取结果。对比发现，特征函数CF4的STA/LTA结果中只有一个比较明显的峰值，与真实的微震到时一致。而特征函数CF2的STA/LTA结果中存在多个比较明显的峰值，且只有一个记录与真实的微震到时一致，其他均为错误微震事件。因此，针对强噪声干扰下的微震数据，利用MLoG滤波方法可以保留原始微震数据形态特征，联合改进的特征函数CF4的STA/LTA方法能有效提高微震数据的抗噪性和到时拾取的准确性。

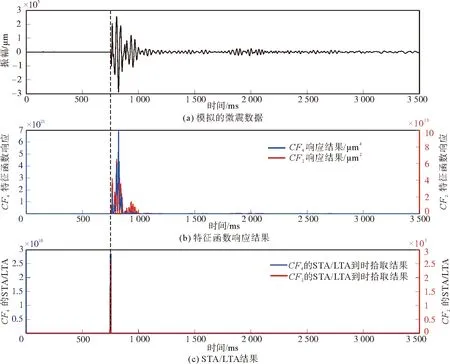
图2 合成数据记录自动到时拾取结果

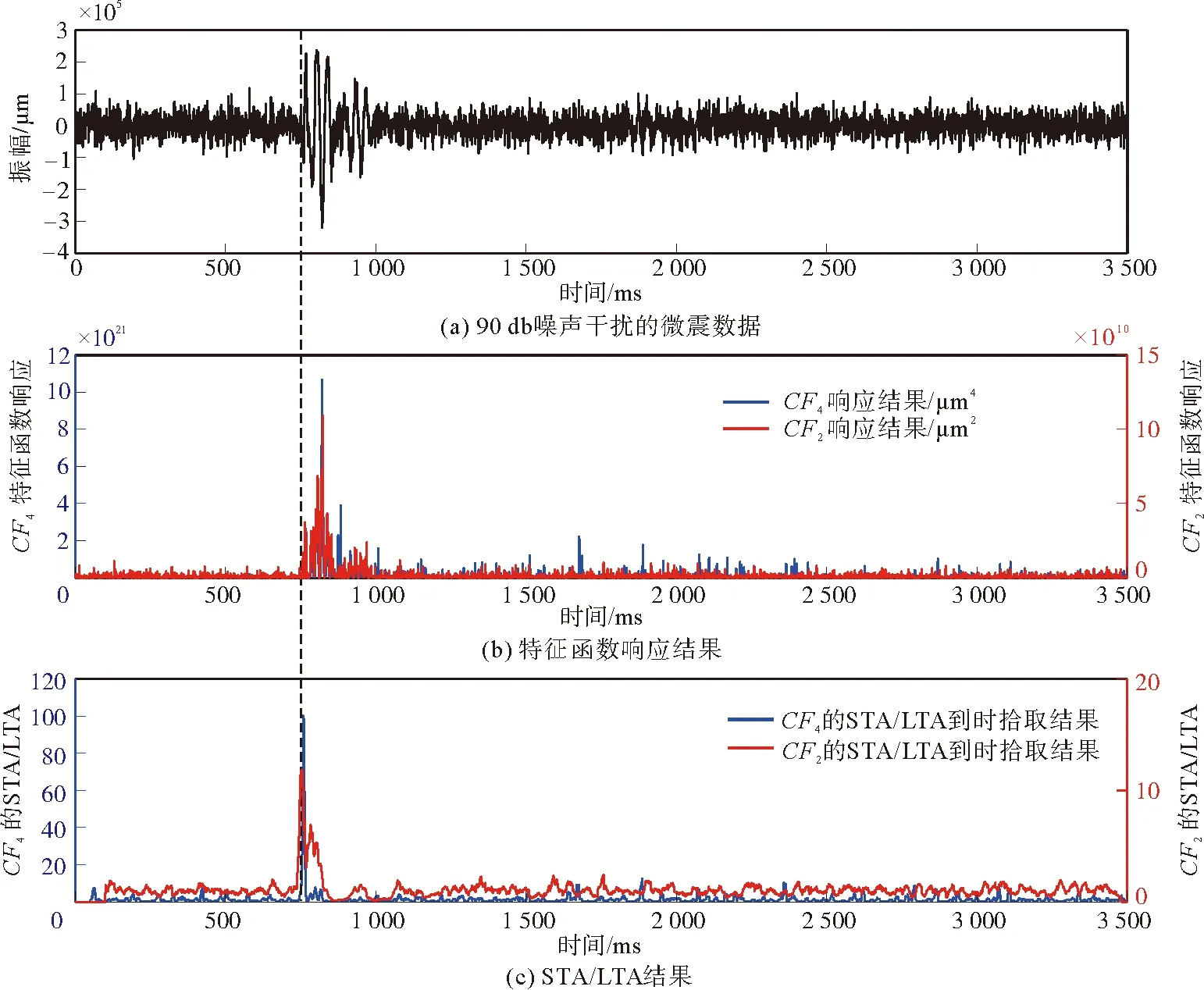
图3 添加90 dB高斯白噪声后的到时自动拾取结果

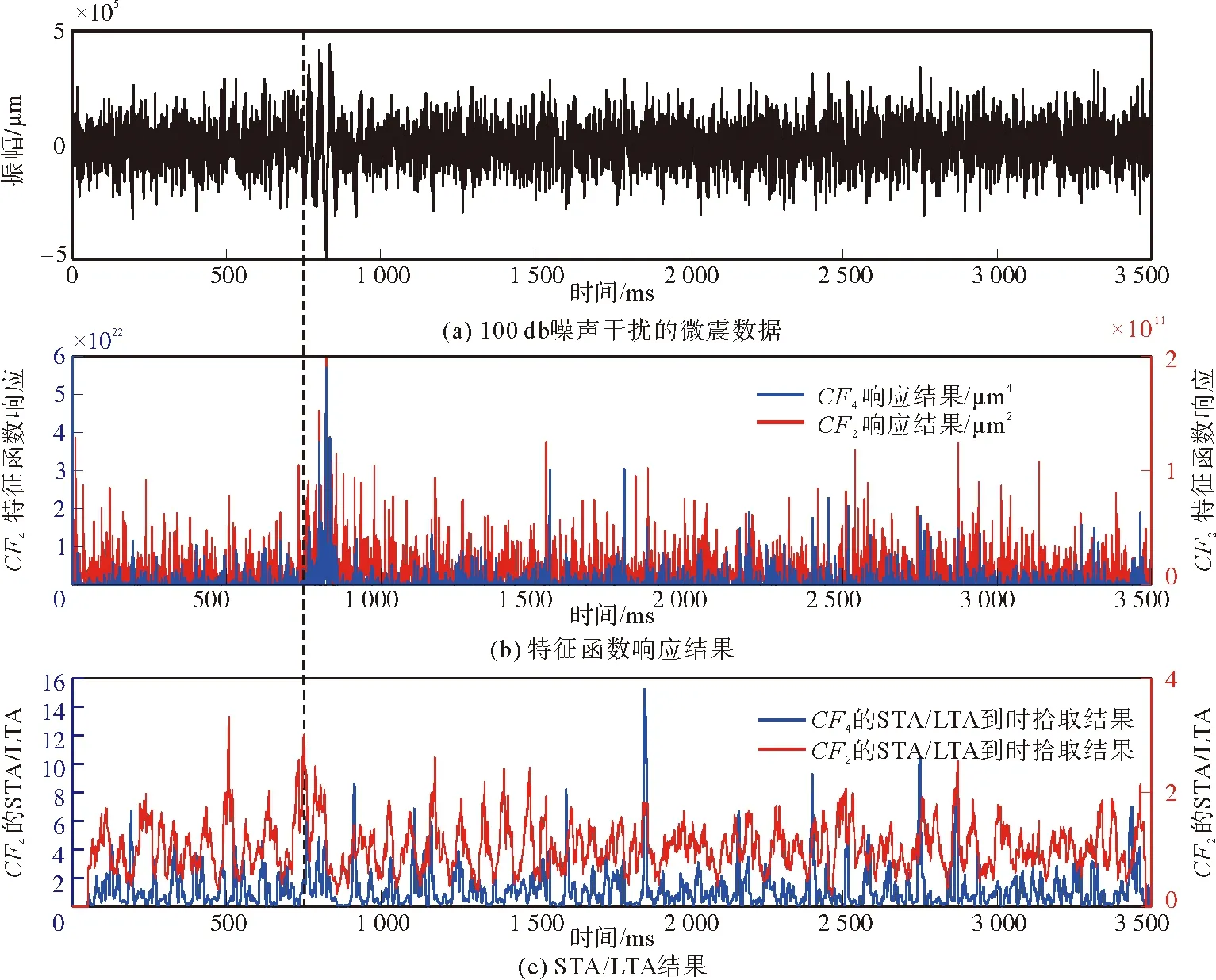
图4 添加100 dB高斯白噪声后的到时自动拾取结果

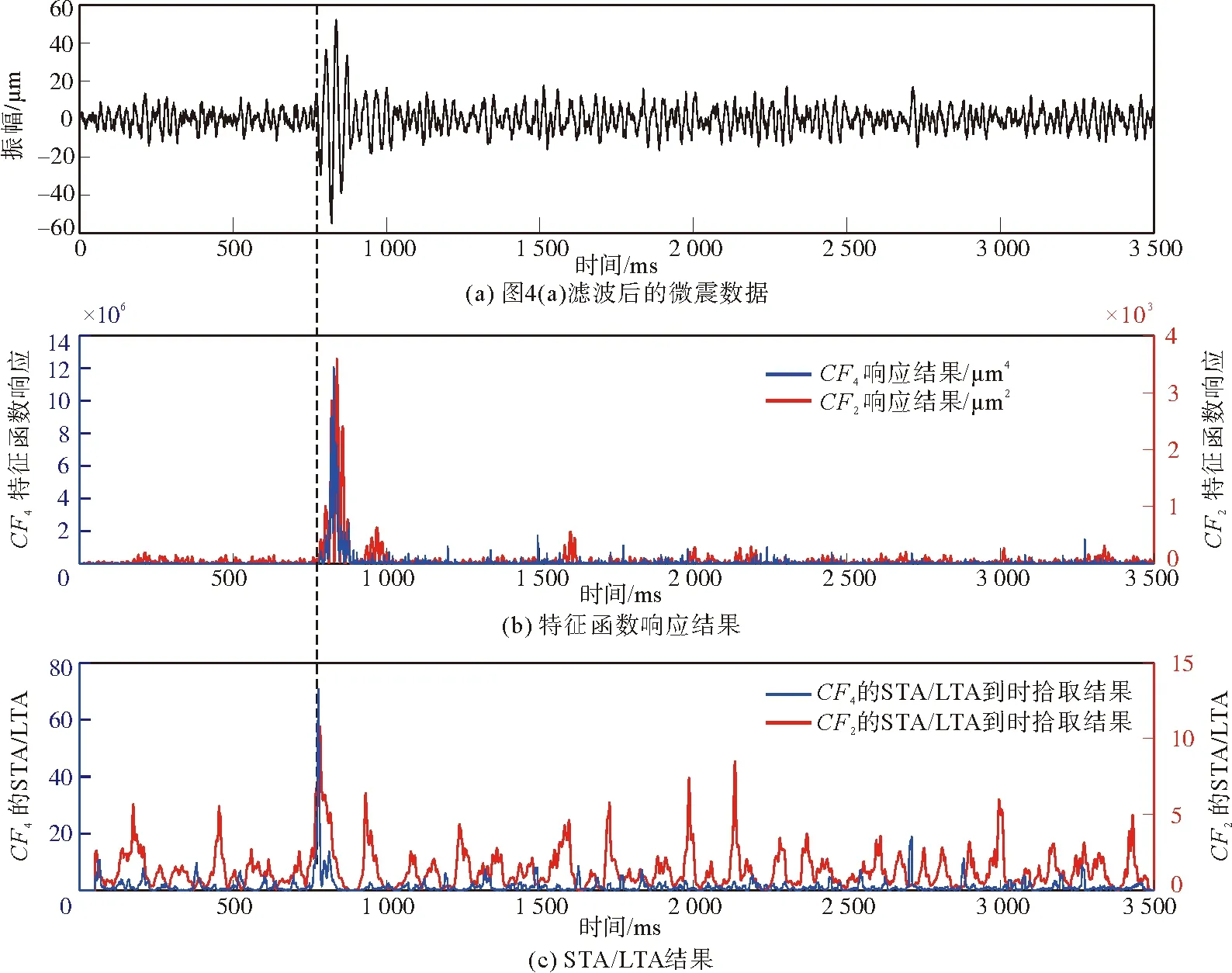
图5 图4(a)滤波后的到时自动拾取结果

3 实测数据应用

某矿区因历经多期构造运动，地质条件复杂，断裂发育。区内发育有固镇—长丰、光武—固镇等正断层，这些断层具有良好的隔水作用，为煤层气聚集储存提供了有利条件。所选用的压裂井是布置在该矿区祁南块段上的一口煤层气试采取芯井。为监测该压裂井附近水力压裂裂缝发育、分布规律等情况，在该区域建立微地震监测系统，记录因连续压裂引起的储层物理特性改变而产生的微地震活动，为矿区地面水力压裂工程成果的考察检验提供指导性建议。

微地震监测系统的采样频率为1 000 Hz，采集到的三分量微地震监测数据见图6和图7中黑线。利用人工拾取的某一个P波到时为16 259 ms。在实测数据应用中，因输入的是三分量微震数据，所以到时拾取结果取三分量微震数据的均值。针对矿区微震数据，首先利用MLoG滤波方法对其进行滤波处理，对应的σ为2.5,n为10，然后分别选取特征函数CF2和CF4计算STA/LTA，STA/LTA曲线的峰值记为微震P波到时。结果见图6和图7。

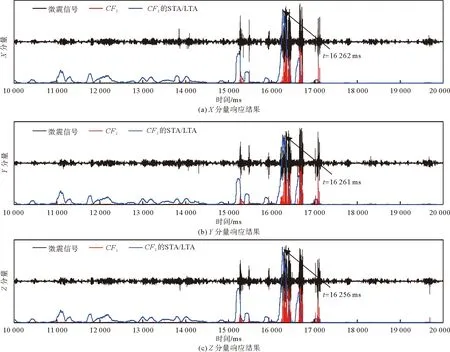
图6 以CF2作为特征函数的STA/LTA监测结果

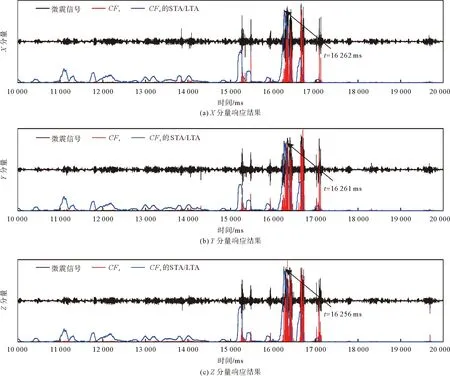
图7 以CF4作为特征函数的STA/LTA监测结果

对比两种结果可知，当微震有效信号首次到来时，采用CF2和CF4作为特征函数计算的STA/LTA曲线幅值相应地存在较大的变化，实现了对微地震有效事件的准确识别。两种特征函数对应的STA/LTA在X、Y、Z分量上拾取的到时相同，分别为16 262、16 261、16 256 ms，计算3个分量到时的均值为16 259 ms，与人工拾取结果一致，证明了该方法在实际应用中的精确性和有效性。

4 结论

本研究提出一种联合改进STA/LTA与MLoG算子的微震P波震相到时自动拾取方法，将其应用于模型数据与实际微震数据进行验算，得出如下结论：

1) 在强背景噪声影响下，本研究改进的特征函数CF4采用高阶幂级数放大微震事件的有效信息，提高了P波到时拾取结果的准确性。

2) 针对弱信噪比的微震数据，在强噪声干扰下引入MLoG滤波算子对背景噪声进行平滑处理，增强信噪比，且在去除随机噪声干扰的同时最大程度保留有效信号形态，联合改进的特征函数CF4的STA/LTA方法能有效提高微震数据的抗噪性。

3) 通过模型数据和某地区微震实测数据试算，证明了本方法相对于传统P波到时自动拾取方法有较强的抗噪能力，具有更高的准确性。