具有时变时滞的离散时间随机非线性系统的有限时间稳定性分析
刘西奎,王继秋,李 艳,庄继晶
(1.山东科技大学 数学与系统科学学院,山东 青岛 266590; 2. 山东科技大学济南校区,山东 济南 250031)
时间延迟现象普遍存在于许多实际系统中,例如:电路、神经网络系统、生物系统、多智能体系统等[1-4]。然而,时间延迟往往会降低动态系统的性能甚至导致系统不稳定[5]。因此,研究时滞系统的稳定性和相关控制问题很有必要。近年来,随着对控制系统等的关注,越来越多的学者开始研究具有区间时变时滞系统的稳定性问题[6-7],目前常用的方法是区间时滞分解法,构造适当的李雅普诺夫函数是研究具有区间时变时滞系统稳定性的关键。有限时间稳定[8-9]和渐近稳定[10-11]是两种不同的稳定概念。有限时间稳定研究的是一个系统在有限时间内的状态行为,需要预先给定系统状态轨迹的界限;而渐近稳定研究的是系统在无限时间的状态行为,不需要预先给出系统状态轨迹的界限。渐近稳定描绘的是系统在无限时间下的性能,而无法反映系统在有限时间下的性能。因此,在工程中有时会出现一个有限时间下性能很差的渐近稳定系统。在实际工程中,人们不仅要关注系统的稳态性能,更要关注系统的暂态性能。为了研究系统的暂态性能,Dorato[12]提出了有限时间稳定的概念。Zhang等[13]引入倒立凸矩阵不等式,研究线性时滞系统的渐近稳定性。文献[14]提出一种新的李雅普诺夫方法分析线性时滞系统的有限时间稳定。文献[15]和文献[16]分别给出连续和离散时间线性时滞奇异系统有限时间稳定/镇定的判据。文献[17]研究连续时间线性时滞系统的有限时间有界跟踪控制问题。
在实际工程中,系统通常会受到一些非线性因素的干扰[18-19]。因此,非线性系统的有限时间稳定问题受到众多学者的关注。Kang等[20]针对具有区间时变时滞和非线性扰动的离散时间系统,研究了系统有限时间稳定问题;构造了一种新的李雅普诺夫-克拉索夫斯基函数,采用离散Wirtinger型不等式、变互式凸组合方法和零等式,推导出改进的有限时间稳定性准则。Stojanovic[21]在文献[20]的基础上,对于具有时变时滞和不确定项的离散时间非线性系统,提出保守性较小的有限时间稳定性判据。文献[22]通过建立新的加权求和不等式,推广了离散的Jensen’s型不等式,提出时滞非线性系统有限时间稳定的充分条件,以保证系统的状态不超过给定的阈值。文献[23]通过引入自由模糊加权矩阵,提出一种与时滞相关的开环模糊系统有限时间稳定性准则,得到保守性更小的矩阵,以确保时滞模糊非线性系统的有限时间稳定性。

基于上述讨论,针对具有区间时变时滞的离散时间非线性随机系统,研究该系统的有限时间稳定问题。首先,给出该随机系统有限时间稳定的定义。其次,提出一种新的李雅普诺夫泛函,其包含双重求和项。采用一个新的有限和不等式处理李雅普诺夫泛函的前向差分,该不等式等同于Jensen’s不等式,但一定程度上降低了保守性。同时,利用线性矩阵不等式给出系统有限时间稳定的充分条件。最后,通过给出数值例子说明结果的有效性。
文中的符号表示如下:N0={-hM,-hM+1,…,-1,0},N={1,2,3,…,N},Rn表示n维欧氏空间,Rn×m表示维数为n×m的实矩阵。对于矩阵P∈Rn×n,P-1和PT分别表示P的逆矩阵和转置,λmax(P)和λmin(P)分别表示矩阵P的最大特征值和最小特征值。P>0(P≥0)表示P是正定(半正定)矩阵。
1 问题分析
考虑具有时变时滞的离散时间非线性随机系统
(1)
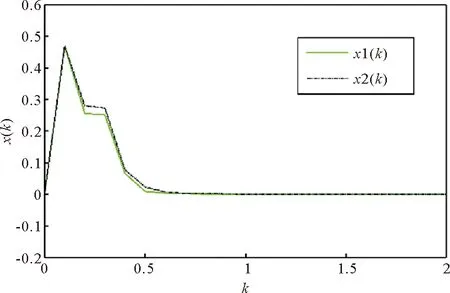
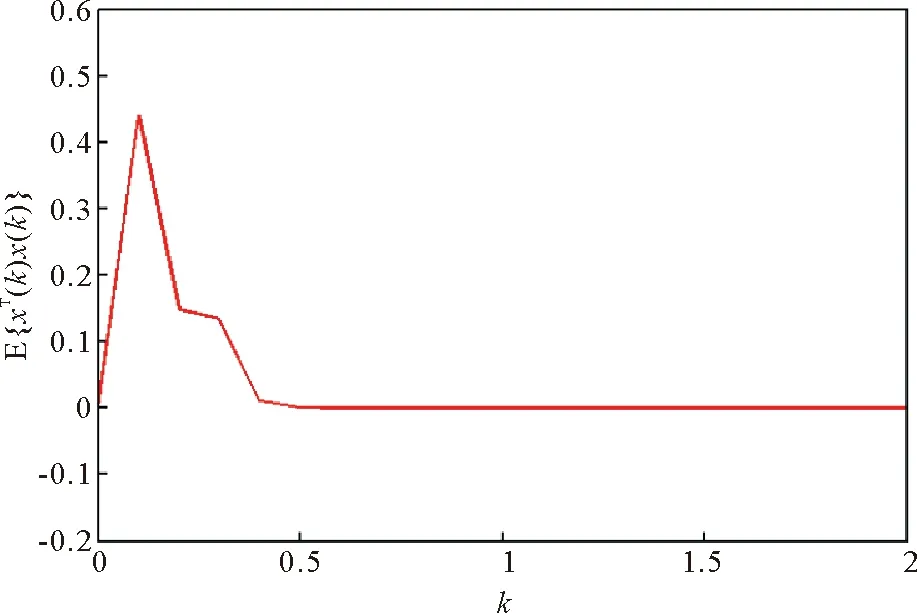
其中:x(k)∈Rn是状态向量;M,Md,D∈Rn×n是具有适当维数的常矩阵;h(k)为区间时变时滞且满足0 (2) g1(x(k),k)和g2(x(k-h(k)),k)分别是对于状态x(k)和离散时滞状态x(k-h(k))的未知非线性扰动,满足条件 其中F和Fd是已知的实矩阵。 如果系统(1)不包含非线性扰动,则得到如下标称系统 (3) 为了研究具有时变时滞的离散时间非线性随机系统(1)的有限时间稳定问题,引入以下定义和引理。 1)T<0; 引理2[36]对于任意适当维数的矩阵U>0,UT>0,U∈Rn×n,S∈Rm×n,正整数h1,h2,h2>h1和正常数γ,满足不等式 其中,y(k)=x(k+1)-x(k),ξ(k)∈Rm×1是适当的向量函数,ρ是正常数且满足 本节将给出系统(1)有限时间稳定与渐近稳定的充分条件。 (4) λ1I (5) γΝ[α(λ2+δ1λ4+δ2λ6)+δ(δ3λ7+δ4λ8)]-β[λ1+δ1λ3+δ2λ5]<0, (6) 其中: Ξ1=(Γij)6×6, Γ66=P+Q12-εdI,Q12=(hM-hm)Q1+hmQ2, (7) (8) 则系统(1)关于(α,β,Ν)有限时间稳定。 证明:构造如下李雅普诺夫泛函 V(k)=V1(k)+V2(k)+V3(k),k∈N, (9) 其中, V1(k)=xT(k)Px(k), 沿着系统(1)的轨迹,分别得V1(k),V2(k),V3(k)的前向差分: E{ΔV1(k)}=E{V1(k+1)-V1(k)} =E{xT(k+1)Px(k+1)+(γ-1)V1(k)-γV1(k)} =E{(γ-1)V1(k)+xT(k)(MTPM+DTPD-γP)x(k)+2xT(k)MTPg1(x(k),k) +2xT(k)MTPMdx(k-h(k))+2xT(k)MTPg2(x(k-h(k)),k) (10) E{ΔV2(k)}=E{V2(k+1)-V2(k)} =E{(γ-1)V2(k)+xT(k)(W1+W2)x(k) -γhMxT(k-hM)W1x(k-hM)-γhmxT(k-hm)W2x(k-hm)}, (11) E{ΔV3(k)}=E{V3(k+1)-V3(k)} (12) =E{(γ-1)V3(k)+yT(k)[(hM-hm)Q1+hmQ2]y(k) (13) 由引理2和(13)得: (14) (15) 其中: 通过式(10)~(15)及不等式(16): (16) 得 E{ΔV(k)}≤E{xT(k)[MTPM+DTPD-γP]x(k) +xT(k)[W1+W2+(M-I)TQ12(M-I)+DTQ12D]x(k) +2xT(k)(MTPMd+(M-I)TQ12Md)x(k-h(k)) +2xT(k)(MTP+(M-I)TQ12)g1(x(k),k) +2xT(k)(MTP+(M-I)TQ12)g2(x(k-h(k)),k) -γhMxT(k-hM)W1x(k-hM)-γhmxT(k-hm)W2x(k-hm) (17) 即 (18) 根据引理1,不等式(4)等价于 (19) 从而式(18)化简为 E{ΔV(k)-(γ-1)V(k)}<0, (20) 进一步计算,得 E{V(k)}<γkE{V(0)},k∈N。 (21) 根据V(k)的定义,有 (22) =α(λmax(P)+δ1λmax(W1)+δ2λmax(W2))+δ(δ3λmax(Q1)+δ4λmax(Q2))。 (23) 由式(6)得 γΝ[α(λmax(P)+δ1λmax(W1)+δ2λmax(W2))+δ(δ3λmax(Q1)+δ4λmax(Q2))] 根据式(21)~(23)及(5),得 即 (24) 考虑不等式(2)及(24),得 E{xT(k)x(k)}<β,k∈N, 故系统(1)关于(α,β,Ν)有限时间稳定。 本研究与文献[20,21]相比,考虑了系统的随机性,进一步讨论了具有区间时变时滞的离散时间非线性随机系统的有限时间稳定问题。 注1构造李雅普诺夫泛函的方法不同于文献[18,20],使用估计延迟状态加权范数的有限和不等式,更精确地估计李雅普诺夫-克拉索夫斯基泛函初值的上界和下界,从而获得保守性较小的稳定性准则。值得注意的是,当D=0时,定理1即为文献[21]中的定理1。因此,本研究的结果更具有一般性。 注2对于随机系统(1),有限时间稳定性准则的保守性受不等式(21),(22)和(23)的限制。考虑具有幂函数γk-j-1的李雅普诺夫函数,得E{V(k)}<γE{V(k-1)},即E{V(k)}<γkE{V(0)}。E{V(0)}<Θ1,E{V(k)}>Θ2,其中Θ1和Θ2分别是E{V(0)}上界的估计值和E{V(k)}下界的估计值,这些估计依赖于参数α,β,N,hm,hM,δ和γ。此方法能精确地估计上界和下界,从而获得保守性较小的有限时间稳定性准则。 特别的,当γ=1时,定理1变为系统(1)渐近稳定的充分条件,即如下推论。 其中: 则系统(1)渐近稳定。 证明:当γ=1时,式(20)变为E{ΔV(k)}<0,从而系统(1)渐近稳定。 在本节,当g1(x(k),k)=g2(x(k-h(k)),k)=0时,定理1变为标称系统(3)有限时间稳定的充分条件,如定理2。 λ1I γΝ[α(λ2+δ1λ4+δ2λ6)+δ(δ3λ7+δ4λ8)]-β[λ1+δ1λ3+δ2λ5]<0, 其中: 则标称系统(3)关于(α,β,Ν)有限时间稳定。 证明:根据定理1及(3),定理2显然成立。 特别的,当h(k)=h时,得到以下推论。 其中: 则系统(3)关于(α,β,Ν)有限时间稳定。 证明:构造如下李雅普诺夫泛函 V(k)=V1(k)+V2(k)+V3(k), 其中: 证明类似于定理1,此处不再赘述。 本节给出两个数值例子来说明所得结果的有效性。 例1给定系统(1)的系数矩阵 考虑以下参数: ε=5,εd=1.21,λ1=0.412 4,λ2=0.413 3,λ3=0.110,λ4=0.125, λ5=0.09,λ6=0.12,λ7=0.21,λ8=0.31,γ=1.41,N=5。 为了验证稳定性,选择以下初始值: 显然,初始值满足以下条件: supj∈{-5,-4,…,-1}(φT(j)φ(j))≤α=3, supj∈{-5,-4,…,-1}(φ(j+1)-φ(j))T(φ(j+1)-φ(j))≤δ=0.2。 根据定理1,解线性矩阵不等式(4)-(6),得系统的状态变量x(k)满足E{xT(k)x(k)}≤69.997 1。图1、图2分别表示状态x(k)的响应及E{xT(k)x(k)}的演化。从图2可以看出,E{xT(k)x(k)}的演化不超过β=69.997 1。因此,随机系统(1)关于(3,69.997 1,5)是有限时间稳定的。 图1 状态变量x(k)的响应Fig. 1 The response of state vector x(k) 图2 E{xT(k)x(k)}的演化 表1中对比了当2≤h(k)≤5,Ν取不同值时,定理1和定理2中参数β的最小上界。可以看出,定理2的β最小上界小于定理1的。因此,没有时变时滞和非线性干扰的系统,其稳定性准则的保守性更小。 表1 当2≤h(k)≤5时,系统(1)中参数β的最小上界 例2为了便于比较,给出标称系统(3)的系数矩阵 及参数λ1=0.412 3,λ2=0.412 4,λ3=0.111,λ4=0.177,λ5=0.09,λ6=0.13,λ7=0.20,λ8=0.32,γ=1.32。 表2表示时滞h(k)∈[2,5],Ν取不同值时,标称系统(3)的参数β的最小上界。从表中可以看出定理2的β最小上界比文献[21]中推论5的更小,但随着N的增大,β的最小上界值越来越接近。可见,在考虑系统的随机性后,N在一定的范围内,其稳定性判据的保守性略小。 表2 当2≤h(k)≤5时,系统(3)中参数β的最小上界 本研究讨论了具有时变时滞的离散时间随机非线性系统的有限时间稳定问题,构造了一个具有幂函数γk-j-1和新的求和项的李雅普诺夫泛函,给出了随机系统有限时间稳定的充分条件。通过使用线性矩阵不等式方法,得到保守性较小的稳定性判据。对于常时滞离散时间随机非线性系统,给出了该系统有限时间稳定的充分条件。最后,通过数值例子证明本研究的结果是有效的。值得注意的是,本研究方法可以应用于其他系统,例如马尔可夫跳跃系统、奇异系统和离散自治系统等。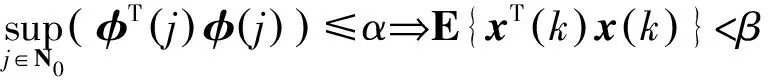
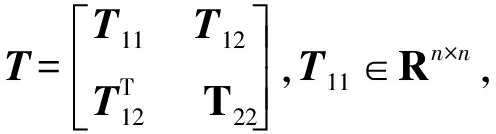
2 具有非线性扰动的随机系统的有限时间稳定
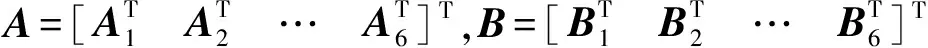
<β[λmin(P)+δ1λmin(W1)+δ2λmin(W2)]。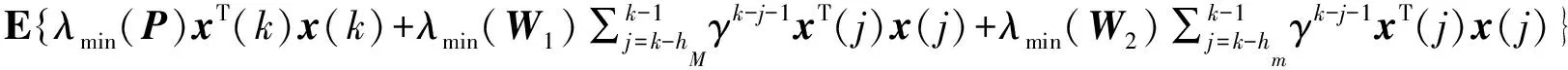
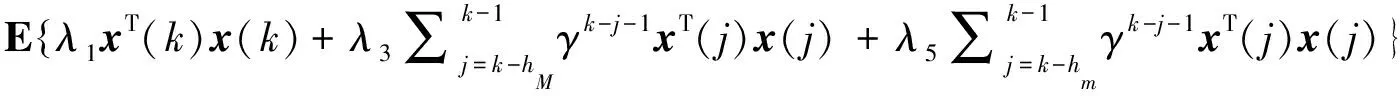
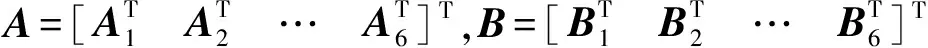
3 标称系统的有限时间稳定
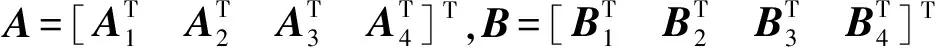
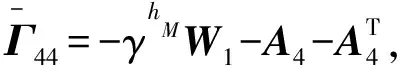
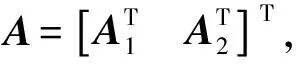
4 仿真例子
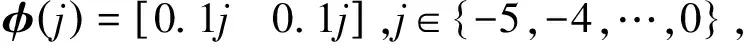
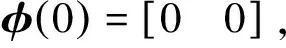


5 结论

