欧洲地区GPS站速度估计及地壳运动分析

李国伟，周茂盛

(1. 山东省国土测绘院 山东 济南 250102; 2. 山东科技大学 测绘与空间信息学院，山东 青岛 266590)

大地测量技术作为监测地壳运动的有效手段之一，其信息获取手段已由常规测量仪器发展为空间测量技术[1]。由于全球定位系统(global positioning system，GPS)相对于其他空间观测技术具有成本低、相对测量精度高、观测方便等优势，已成为目前主要的形变观测手段，被广泛应用于区域地壳形变研究[2]、强地震位移场检测[3-4]、慢地震位移研究[5-6]以及冰后期回弹分析[7]等领域，并发挥了重要作用。

Altamimi等[1]利用多种空间大地测量技术，建立国际地球参考框架(international terrestrial reference frame，ITRF)ITRF2008和全球板块运动模型[8]。国内学者[9-10]采用GPS观测资料，建立中国地壳运动速度场，并分析构造变形规律。Grenerczy等[11]利用GPS数据分析欧洲地壳运动规律。Santamaria-Gomez等[12]计算全球GPS测站的站速度，并利用垂直方向地壳形变规律，进行海平面绝对变化规律的研究。

要分析地壳运动规律，必须首先获取高精度的站速度。目前高精度全球导航定位系统(global navigation satellite system，GNSS)数据处理软件一般采用序贯平差或卡尔曼滤波方法进行线性站速度估计。坐标时间序列分析软件采用最小二乘谱分析拟合线性站速度，采用极大似然估计处理时间序列的随机部分[13-14]。GPS坐标时间序列呈闪烁噪声+白噪声+随机游走噪声的特性，站速度精度受噪声模型的影响较大，不恰当的随机模型可导致速度不确定度的有偏估计[15-18]。站速度估计与坐标时间序列分析密不可分。

奇异谱分析(singular spectrum analysis，SSA)[19]作为一种数字信号处理技术，在气候学、测量学[20]、海洋学[21]等领域都有应用。郭金运等[22]利用SSA实现了相对重力观测数据中固体潮的可靠提取。王鹏程等[23]利用SSA分析了汶川地震震前地倾斜数据，发现了震前异常。史坤朋等[24]利用SSA进行了电离层总电子含量预测，牛余朋等[25]利用SSA进行近海海平面变化预测，都取得了良好效果。Zhou等[26-27]采用多通道奇异谱分析(multi-channel singular spectrum analysis，MSSA)分离了GPS坐标时间序列中的共模误差，改善了GPS坐标时间序列精度和站速度估计精度。

本研究提出奇异谱分析和最小二乘拟合相结合的方法估计测站速度，先利用奇异谱分析将坐标时间序列构成成分进行分离，再采用最小二乘拟合重构的趋势项估计GPS站速度，最后对GPS站速度估计结果进行精度评定，分析欧洲地区地壳运动规律。

1 数据及方法

1.1 GPS数据

欧洲地区约70个测站的GPS数据由http://www.sonel.org[12]提供，采样率为30 s，时间跨度为6年(2011—2016)，点位如图1所示。

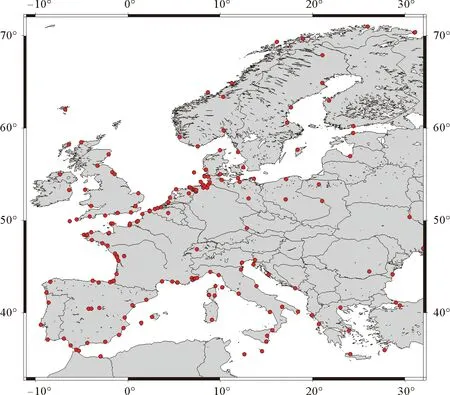
图1 测站点位图

1.2 GPS数据处理及时间序列预处理方法

GAMIT/GLOBK10.7主要解算策略为[28]：采用国际GNSS服务组织(International GNSS Service，IGS)最终星历，选择轨道及基站松驰约束，卫星截止高度角为10°，观测数据采样间隔为30 s，采用无电离层组合(LC组合)，采用Saastamoinen模型及VMF1映射函数。网平差选取ITRF2008框架下稳定的IGS站作为起算点，采用最小约束方式进行解算。

坐标时间序列预处理主要工作是粗差数据剔除和缺失数据补全。对坐标时间序列进行拟合，以3倍标准差为阈值，进行粗差的识别和剔除。利用SSA插值来恢复缺失数据[29-32]，插值截止的中误差阈值为0.01 mm。

1.3 站速度估计方法

1.3.1 坐标时间序列SSA分解

SSA方法对构造的轨迹矩阵进行分解，提取时间序列不同成分[19]。GPS坐标时间序列的时滞轨迹矩阵X为：

(1)

其中：N为时间序列的长度；M为窗口长度；K=N-M+1。式(1)中Xi可表示为：

(2)

对矩阵XXT进行奇异值分解，计算其特征值λ1,…,λM，对应的特征向量为U1,…,UM。设d=rank(X)，则时滞矩阵X可变换为：

X=Xc1+Xc2+…+Xcd，

(3)

按信号类型将初等矩阵Xck分为m个不相交的子集，即分组为A1,A2,…,Am，若子集Ai包含ap个初等矩阵，则分组Ai的合成矩阵可表示为：

XAi=Xa1+Xa2+…+Xap。

(4)

对于X用合成矩阵表示的公式为：

X=XA1+XA2+…+XAm。

(5)

将XAi对角平均化，公式为：

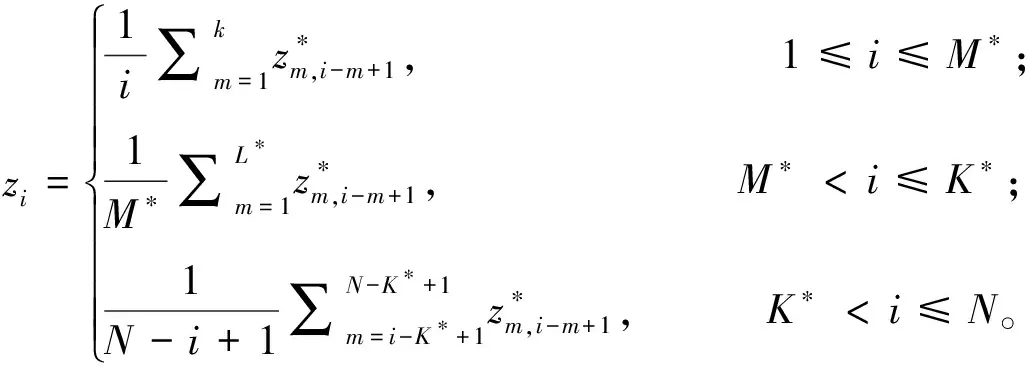
(6)

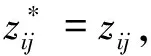
完成对角化后，重构新的时间序列，对其进行信号分离，可得特征值大小不同信号。

1.3.2 站速度最小二乘拟合

常规采用最小二乘谱分析方法估计GPS站速度[13-14]，同时考虑趋势项、周年项、半年项进行估计，如式(7)所示：

y(ti)=x0+vx·ti+Aa(ti)+Asa(ti)+ε(ti)。

(7)

式中：y(ti)为趋势项；x0为初始值；vx为速度值；Aa(ti)为周年项；Asa(ti)为半年项；ε(ti)为声项；ti(i=1,…，n)为年积日。

本研究利用SSA分析GPS坐标时间序列，重构趋势项，实现了趋势项与周年项、半年项及噪声项的分离，趋势项表示为：

T(ti)=x0+vx·ti。

(8)

将分离后的趋势项作为观测值，按式(9)估计站速度：

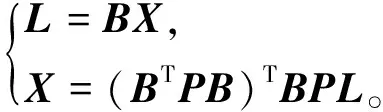
(9)

2 数据处理和结果

2.1 GPS数据解算及时间序列预处理

GAMIT基线解算精度如表1所示，双差数据处理的标准化均方差(normalized root mean square，NRMS )均优于0.19，相对精度平均值在10-9量级。GLOBK网平差精度如表2所示，网平差各坐标分量精度平均值均优于4.3 mm，标准差均优于4.5 mm，极少数测站由于观测环境不理想，坐标精度为cm级，在后续数据处理时作为粗差被剔除。由上述分析可知，解算结果可用于高精度地壳运动规律分析。对欧洲区域2011—2016年单日解坐标时间序列(ITRF2008框架)，按1.2节中粗差剔除和缺失数据插值方法进行预处理，保证坐标时间序列的可靠性和完整性。

表1 基线精度统计

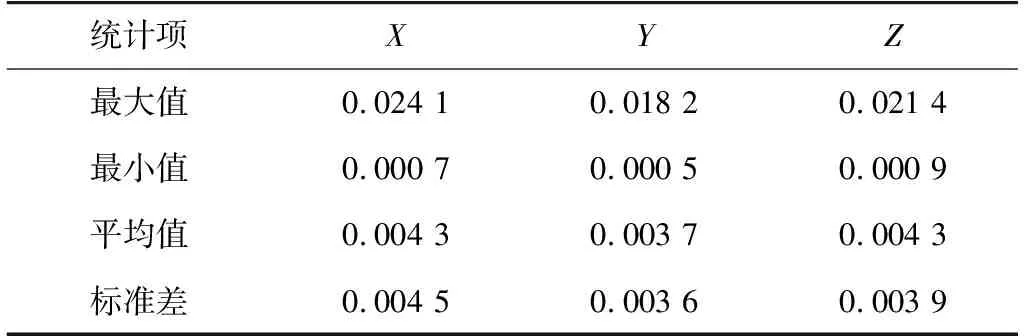
表2 网平差精度统计

2.2 站速度估计

2.2.1 坐标时间序列SSA分析

采用SSA方法(1.3.1节)分析GPS坐标时间序列，由于篇幅限制，从实验数据中选取两个测站的U方向的分析结果进行成图展示，如图2、图3所示。SSA分解后的各个重构成分按照特征值的贡献率大小依次排列，GPS坐标时间序列中特征值贡献率由大到小为趋势项、周年项、半年周项和噪声项，且除了趋势项之外，其他重构成分都是成对存在的。图2和图3中， (a)图为趋势项，(b)(c)图为周年周期项，(d)(e)图为半年周期项，其余视为噪声。

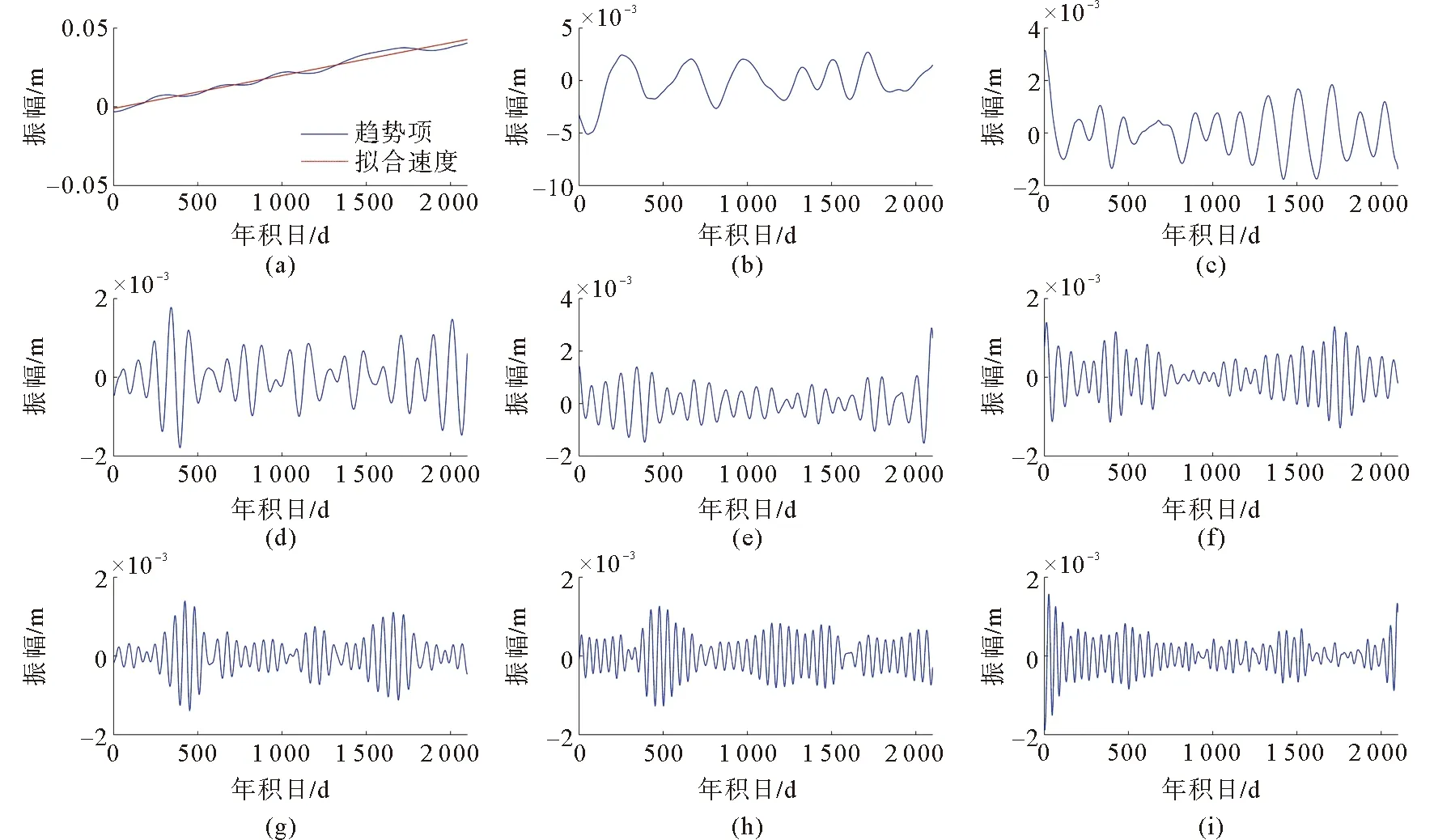
图2 HONS站U方向SSA和最小二乘拟合结果

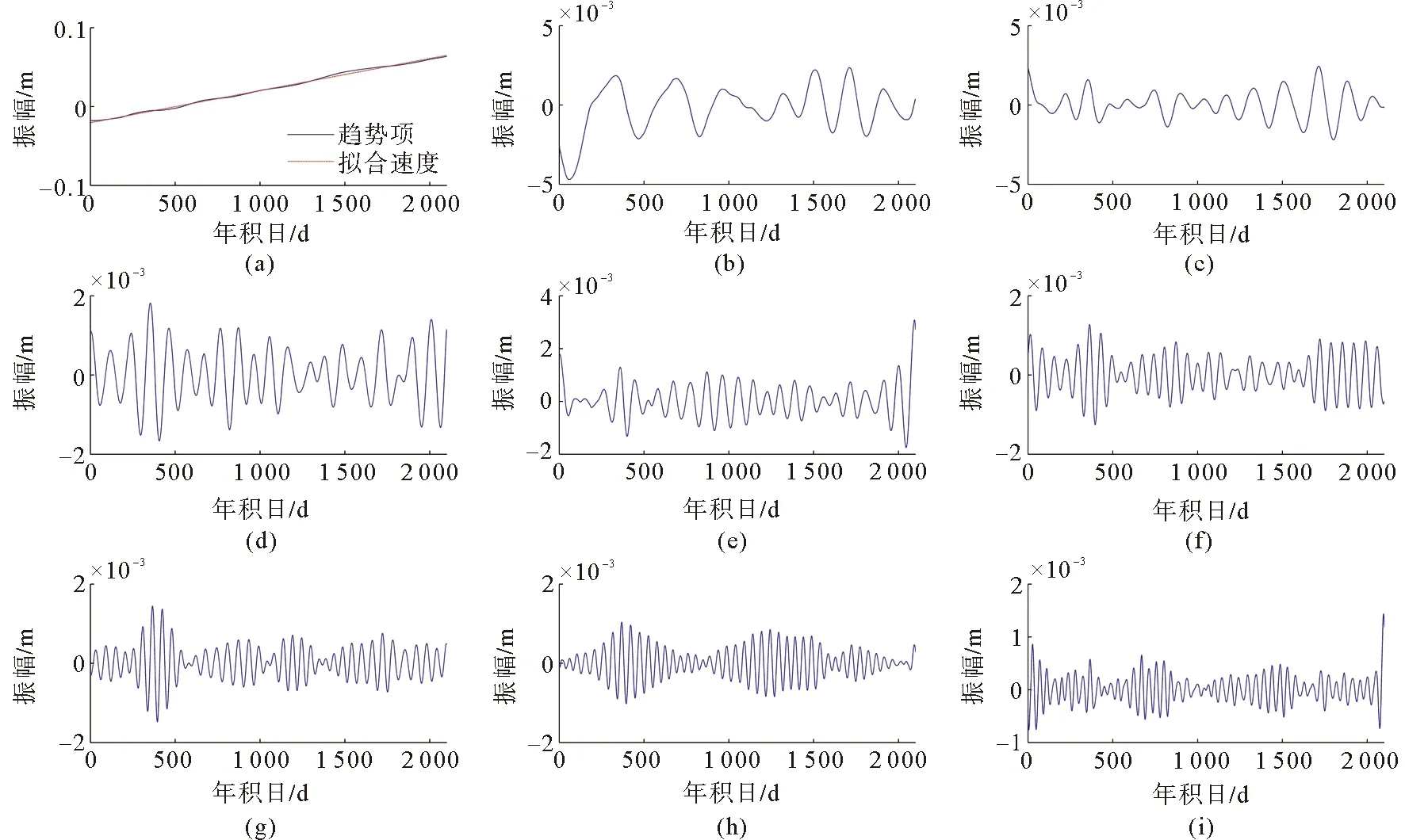
图3 VIKC站U方向SSA分析和最小二乘拟合结果

2.2.2 站速度最小二乘拟合

利用SSA重构的趋势项，按1.3.2节中式(9)估计了GPS站速度，精度统计结果如表3所示，各方向速度估计的中误差平均值均优于0.45 mm/yr，说明站速度估计精度较高，能够满足地壳运动研究的要求。采用最小二乘谱分析方法估计的GPS站速度中误差统计结果如表4所示。两种方法估计的GPS站速度差值统计如表5所示。由表3～5可见，SSA和最小二乘拟合相结合的方法估计GPS站速度的精度优于最小二乘谱分析方法，说明先采用SSA将时间序列的趋势项进行分离重构，再对趋势项进行最小二乘拟合，一定程度上避免了周期项和噪声对站速度估计的影响。

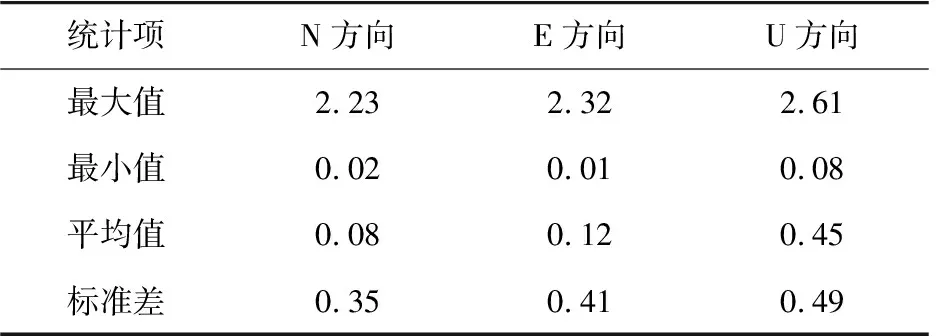
表3 SSA结合最小二乘方法站速度估计中误差统计

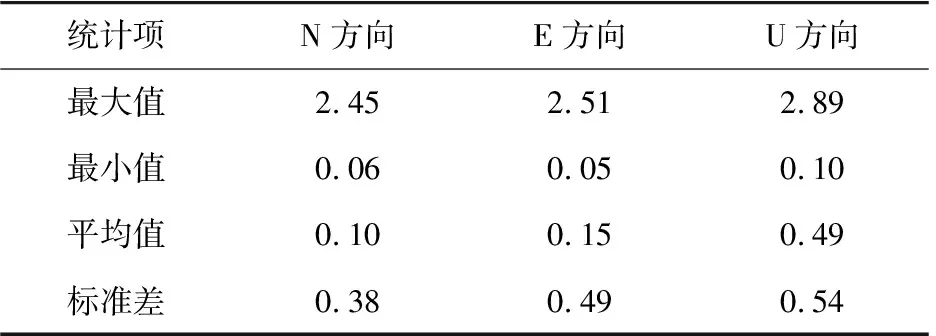
表4 最小二乘谱分析方法站速度估计中误差统计

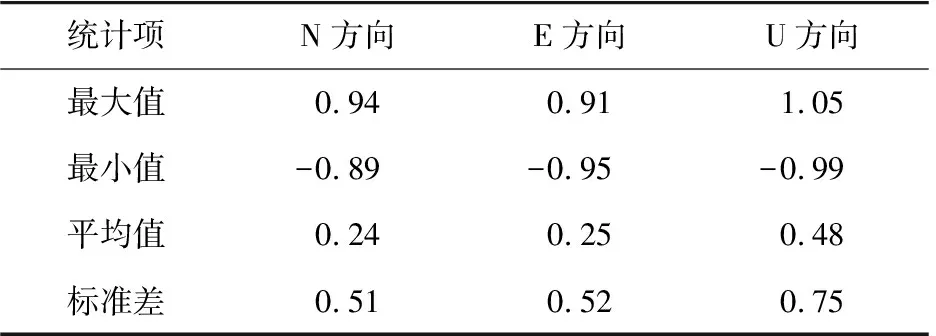
表5 基于SSA方法与最小二乘谱分析的站速度差值统计

SONEL公布的GPS站速度参考框架为ITRF2008，由平均11年的GPS数据估计得出(http://www.sonel.org)。将其作为参考进行对比，结果如表6所示。可见，本次估计的站速度和SONEL速度的差值较小，差值的平均值均小于0.6 mm/yr，标准差均优于1 mm/yr，外附精度较好。

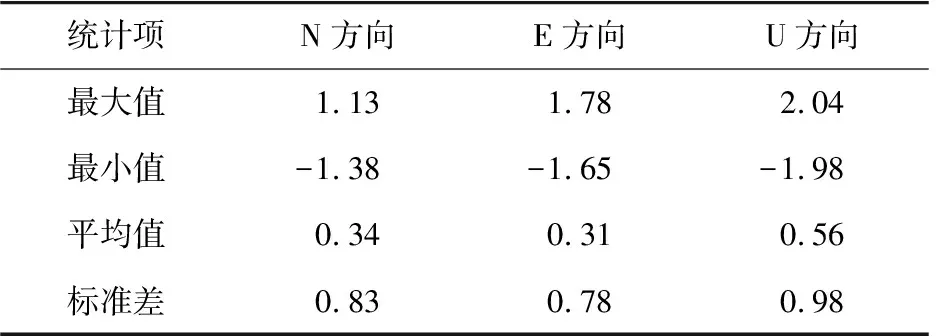
表6 本次估计的站速度与SONEL速度的差值统计Tab. 6 Statistical result of difference between station velocity in this paper and SONEL velocity mm/yr

综上所述，利用SSA和最小二乘拟合相结合的方法估计的站速度是可靠的，其站速度估计结果可以用于地壳运动研究。

2.3 地壳运动分析

利用2.2节GPS站速度估计结果，进行欧洲区域地壳运动规律分析。由图4和图5可以看出，就水平运动而言，欧洲大部分地区以大约20 mm/yr的速度向西北方向运动，且高纬区域的运动速度略小于低纬区域。就垂直运动而言，北纬45°以南的欧洲地区呈下降的运动趋势，且大部分地区运动速度在5 mm/yr以下；北纬45°以北则呈上升的趋势，且随着纬度的增高，上升速度也在变大，靠近北极圈的部分地区的上升速度达20 mm/yr，越靠近北极圈的地区受到冰后回弹的影响越大，上升速率也会越大。本研究得到的欧洲地区水平和垂直地壳运动规律分析结果与Altamimi等[1]、Grenerczy等[11]及Santamaria-Gomez等[12]的研究结果相吻合。

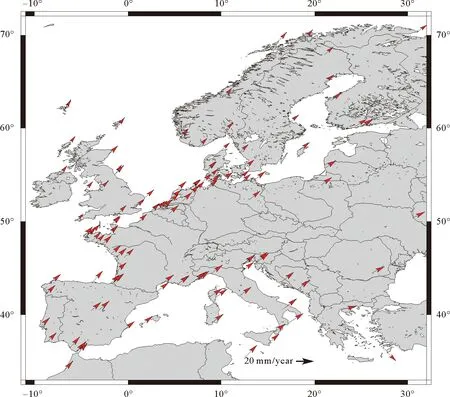
图4 欧洲地区水平速度

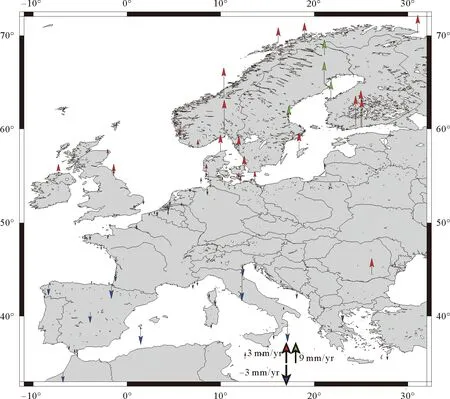
图5 欧洲地区垂直速度

3 结论

利用GAMIT/GLOBK10.7对欧洲区域GPS观测数据进行解算，基线相对精度平均值在10-9量级，解算结果满足高精度地壳运动规律分析的要求。在此基础上利用SSA和最小二乘拟合相结合的方法进行了GPS站速度估计，中误差的平均值均小于0.45 mm/yr，优于常规最小二乘谱分析方法的估计精度，说明新方法一定程度上避免了周期项和噪声对站速度估计的影响。将估计结果与SONEL站速度对比，平均差值均小于0.6 mm/yr，外附精度较好。基于以上数据，分析欧洲地区地壳运动：水平方向，欧洲大部分地区以大约20 mm/yr的速度向西北方向运动；垂直方向，北纬45°以南的欧洲区域呈下沉的趋势，且大部分区域运动速度小于5 mm/yr，北纬45°以北则呈上升的趋势，且随着纬度的增高上升速度也在变大，靠近北极圈的部分地区的上升速度达20 mm/yr。