直线导轨渐进感应淬火过程多物理场耦合分析
肖慈超,贺连芳,李辉平
(山东科技大学 材料科学与工程学院,山东 青岛 266590)
《国家中长期科学和技术发展规划纲要(2006—2020年)》把高档数控机床列为重大专项,重点研发大型、精密、高速数控装备和数控系统,改变大型、高精度数控机床大部分依赖进口的现状,满足机械、航空航天等方面的工业发展需求。与国外产品相比,国产滚动直线导轨存在残余应力大、淬火畸变大、精度保持性差等问题,已成为制约我国高档数控机床发展的瓶颈。直线导轨与钢球的接触面在使用过程中要承受较大压力,因而要求接触面具有较高硬度;另外还要求直线导轨心部具有较好的韧性。为了保证直线导轨具有较高的综合力学性能,感应淬火是最理想的热处理方法之一[1]。感应淬火是一个涉及电磁、温度、相变和应力等多物理场耦合的高度非线性过程。传统检测技术仅能检验零件感应淬火后的最终结果,很难实时描述热处理过程中材料微观组织演变规律[2]。随着计算机硬件性能不断提高和数值模拟软件的发展,通过虚拟热处理技术可深入了解感应淬火过程中温度、相变、应力/应变等物理场量演变,为感应淬火工艺的设计及优化提供较好的理论依据和技术指导。
针对相关零件的感应淬火工艺,许多学者利用计算机技术进行了仿真研究。Li等[3]利用Marc软件对55CrMo丝杠的感应淬火工艺进行了模拟和优化,大幅度改善了淬硬层分布的均匀性,提高了丝杠的寿命和精度保持性。针对感应加热过程,Luo等[4]提出一种基于逆向传热模型的显式有限差分法计算感应加热过程的热流,计算结果与实验结果吻合。胡延平等[5]利用ANSYS软件模拟了多点式中频感应加热过程,用激励电流的表格法加载近似地替代工件的周期性旋转,得到工件温度场随时间的变化规律。Tong等[6]基于“电-磁-热-机”多物理场耦合,模拟42CrMo齿轮异步双频感应淬火过程,结合数值模拟得到的温度和微观组织,揭示了齿轮在中频加热下齿根硬化的根本原因。Dietma等[7]利用有限元方法模拟齿轮的多频感应淬火温度场,基于Johnson-Mehl-Avrami(JMA)方程和Kubelka-Munk(K-M)模型描述感应淬火过程的相变现象,结果表明:数值模拟结果与实验结果吻合较好。数值模拟除了可以得到零件的温度和相变情况,还可以得到零件内部的应力和应变[8-9]。
对于感应淬火工艺数值模拟,多数学者是针对感应器与零件之间没有相对运动的感应淬火过程,而且多是简化为轴对称问题进行研究。但是,直线导轨无旋转对称轴,而且感应器及喷水器与导轨之间有持续的相对运动,是一种渐进式感应淬火过程,因而其模拟过程较齿轮、丝杠、轴类零件等的模拟过程更为复杂。本研究通过构建直线导轨的渐进式感应淬火三维有限元模型,基于非等温JMA相变方程描述导轨感应淬火过程的相变,并对感应淬火过程进行“电-磁-热-机”及相变过程的多物理场耦合分析,优化设计导轨的感应淬火工艺参数,并将数值模拟结果与实验结果进行对比。研究结果可为直线导轨感应淬火工艺参数的设计提供一定的理论依据和技术指导。
1 感应淬火工艺有限元模型及数学模型
1.1 有限元模型
LG系列直线导轨副是一种滚动导引,采用4列圆弧接触式及45°接触角的钢球接触设计,由钢球在滑块与直线导轨之间作无限滚动循环,使得负载平台能沿着导轨作高精度线性运动,摩擦系数约为滑动导引的2%,定位精度可达到微米级。实验及数值模拟过程中,所采用的LG35型直线导轨的截面如图1所示,材料为45钢,感应淬火前的材料先调质(淬火+高温回火),基体组织为回火索氏体。图1中以红色实线标记的轮廓为直线导轨与钢球的接触面。45钢的热物性参数如表1所示。
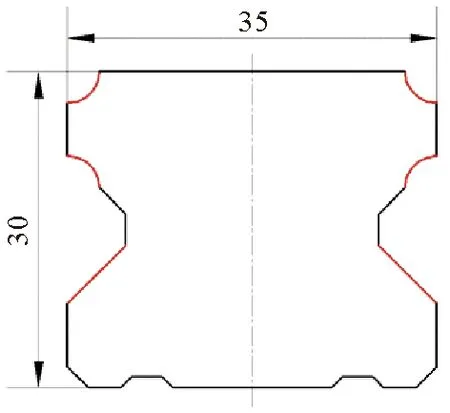
图1 LG35型导轨横截面图
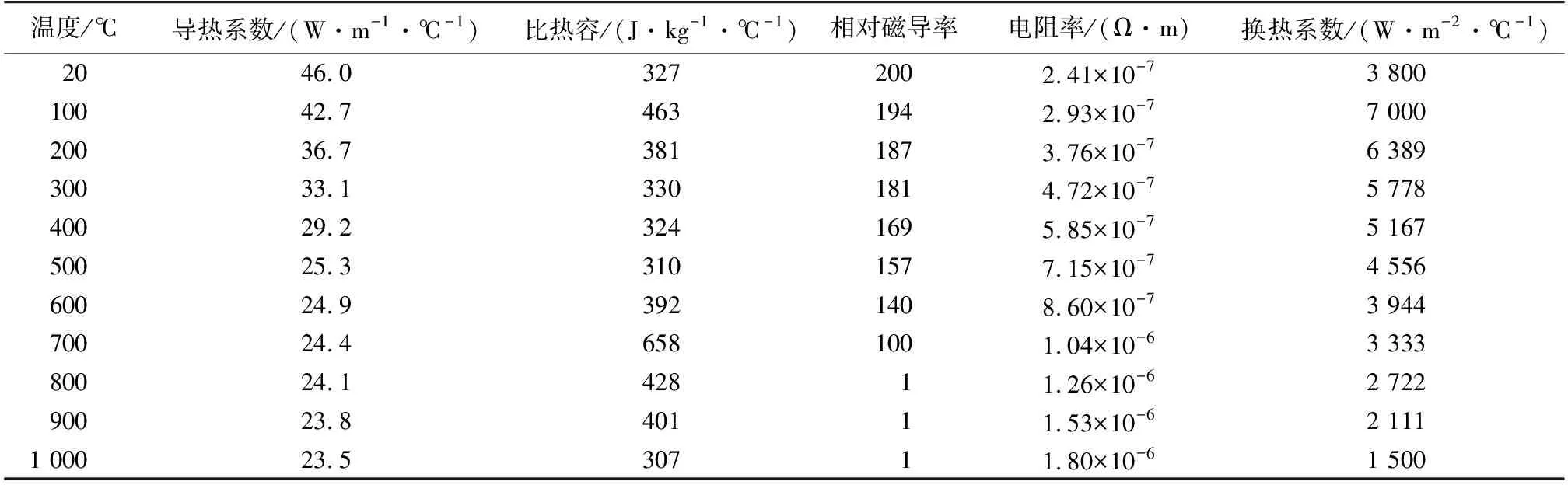
表1 45钢热材料参数
由图1可见,直线导轨轮廓左右对称,但是上下不对称。这种结构若采用图2(a)所示的单感应器包围导轨截面的方法进行整体淬火,容易沿上下方向产生弯曲,影响直线导轨的形状精度。为了保证直线导轨的形状精度,而且保证接触面能达到要求的硬度,采用双感应器对直线导轨左右两侧同时感应淬火。在感应加热过程中,为避免直线导轨表面区域过热,且保证接触面的奥氏体化深度达到设计要求[3],采用了带间隙的双感应器。为了利用导轨心部的热量对导轨表面的马氏体进行余热自回火,喷水冷却器与感应器有一定的距离,如图2(b)。导轨感应淬火过程的三维有限元模型如图3所示。有限元模型包含235 747个四面体和六面体单元,78 524个节点。感应淬火过程中,喷水冷却器覆盖的区域为第三类边界,界面换热系数取自文献[10];其他区域为辐射边界,界面换热系数的计算公式为:
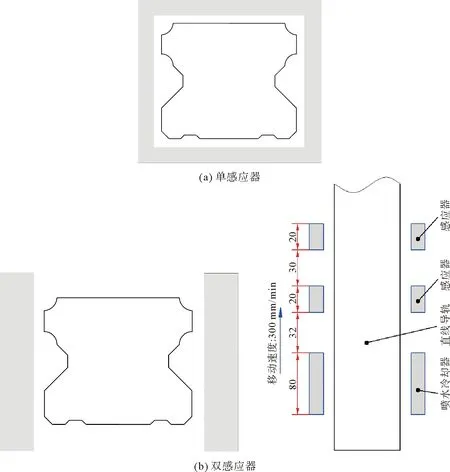
图2 渐进式感应淬火示意图
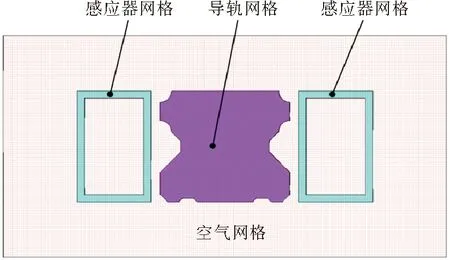
图3 LG35直线导轨感应淬火有限元模型
(1)
其中:Ts为导轨表面温度,K;Tf为环境温度,K;σ为Stefan-Boltzmann常数,值为5.768×10-8W·m-2·K-4;ε为工件表面辐射率。
1.2 数学模型
1.2.1 相变模型
在感应加热过程中,奥氏体体积分数可用JMA方程[11-12]描述为:
f=1-exp(-ηn) ,
(2)
(3)
其中:Q为45钢相变激活能;n为JMA指数;k0为指前因子;T为导轨温度,K;t为相变时间,min;f为奥氏体的体积分数;R为气体常数,8.314 J·mol-1·K-1。
对于感应加热过程中的非等温奥氏体化,式(3)可通过对相变时间积分的方法得到,也可以将非等温过程看成很多个等温过程,通过对离散时间步求和的方式得到[3,13]:
(4)
(5)
其中:T(t)是温度随时间变化的函数,Δt是时间步长,Ti是第i步时的温度。
马氏体相变是非扩散型转变,转变量决定于温度而与时间无关。转变量与温度的关系可表示为[14]:
V=1-exp[-α(Ms-T)] 。
(6)
其中:Ms为马氏体点,α为常数。
1.2.2 相变初应变模型
对于感应淬火过程,材料的全应变增量包括弹性应变增量、塑性应变增量、由温度变化引起的应变增量、相变引起的应变增量和相变塑性引起的应变增量:
(7)
其中:上标e、p、t、tr和tp分别表示弹性、塑性、热、相变、相变塑性,温度变化、相变和相变塑性使感应淬火过程成为一个材料高度非线性问题。
由相变引起的初应变可表示为:
(8)
(9)
其中:βi为相变膨胀系数列阵,是与组织成分有关的系数;dξi为新相的增量;ρA是奥氏体的密度;ρk是相变后的铁素体、珠光体、贝氏体和马氏体的密度。
以张量的形式表达相变塑性与应力和组织转变量的关系式[15]为:
(10)
其中:K为系数,σ′为应力偏量张量,ξi为新相组织的百分比。
2 结果分析与讨论
根据热分析中得出的温度,利用APDL语言进行二次开发,根据式(2)~(5)计算得到感应加热过程中导轨表面的奥氏体体积分数。为了提高奥氏体体积分数的计算精度,在节点的温度达到奥氏体化温度时采用杠杆定理确定达到奥氏体化的具体温度和时间。在感应加热过程中,由于奥氏体只在导轨表面区域生成,而且随后的喷水冷却可保证感应加热过程中生成的奥氏体完全转变为马氏体[1],因而根据式(6)计算冷却过程中马氏体的生成过程。
在感应淬火过程中,导轨内部存在的热应变、相变应变和相变塑性等初应变均会引起导轨内部产生复杂的应力场。通过ANSYS软件对“电-磁-热”三个物理场量进行直接耦合分析,并与相变和应力/应变两个物理场量进行间接耦合(顺序耦合)分析。耦合分析过程中,根据式(8)~(10)计算由相变引起的初应变和相变塑性。本研究所用模型和公式中的材料参数取自文献[1,10]。通过大量的数值模拟,得到一组较理想的工艺参数,可保证LG35直线导轨截面淬硬层深度适中且均匀。电流频率为8 000 Hz,电流密度为6×108A/m2,两个感应器之间的距离为30 mm,第二感应器与喷水器之间的距离为32 mm,喷水冷却器的宽度为80 mm,感应器和喷水器与导轨之间的相对运动速度为300 mm/min,如图2(b)所示。
2.1 渐进式感应淬火过程的温度场
图4展示了感应淬火开始30 s后直线导轨不同区域的温度分布云图。由图4可见,随着感应器和喷水器的移动,导轨表面在第二感应器感应加热时升温至900 ℃以上;由于淬火介质的作用,喷水器覆盖区域的导轨表面由最高温度快速下降至100 ℃左右,实现直线导轨的感应淬火。
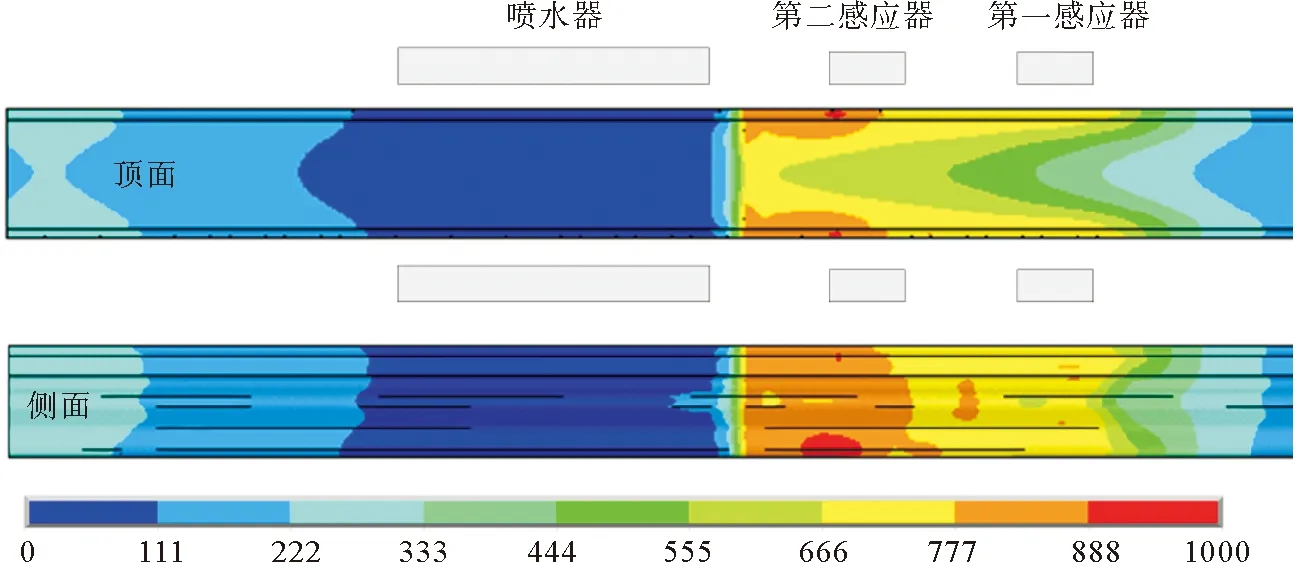
图4 导轨的温度分布(30 s)
导轨截面A、B和C三个位置距离表面不同深度的温度曲线如图5所示,截面在不同时刻的温度云图如图6所示。随着第一感应器逐渐接近截面,截面各处开始升温,23 s时A、B和C处表面温度分别为779.5、677.5和769.5 ℃。由于B处表面与感应器之间的距离大于A和C两处,B处的温度明显低于A和C两处。当第一感应器离开截面后,截面处于两个感应器之间,由于表面的热辐射和热量向截面内部传递,截面表面A、C两处的温度有所下降;由于A和C处的热量向内部和B处传递,B处表面温度在短暂降温后快速升温至787.4 ℃。随着第二感应器接近截面,A、B和C三处温度继续上升,35 s时三处表面温度分别为892.6、865和923.4 ℃。当第二感应器离开截面,截面处于第二感应器和喷水器之间,由于表面的热辐射和表面热量向内部传递,截面表面A、C两处的温度分别下降至840.8和860.4 ℃;由于A和C处的热量向内部传递,B处表面温度在短暂降温后又快速升温至850.4 ℃。当喷水器作用于截面处时,由于冷却介质的作用,截面温度迅速下降;另外,开始喷水冷却时A、B和C三处的表面温度相差不大,这有利于减少导轨的淬火畸变[1,4]。由此可见,采用带间距的双感应器可改善导轨表面温度的均匀性,提高导轨表面奥氏体化程度的均匀性,减少导轨的淬火畸变。
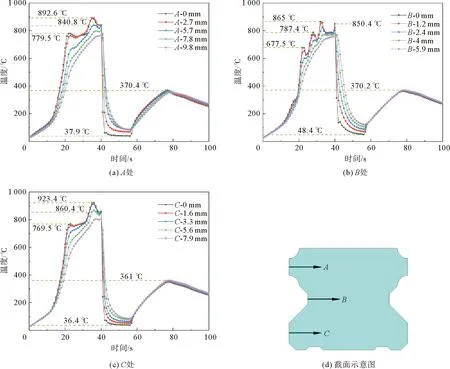
图5 截面不同位置的温度曲线
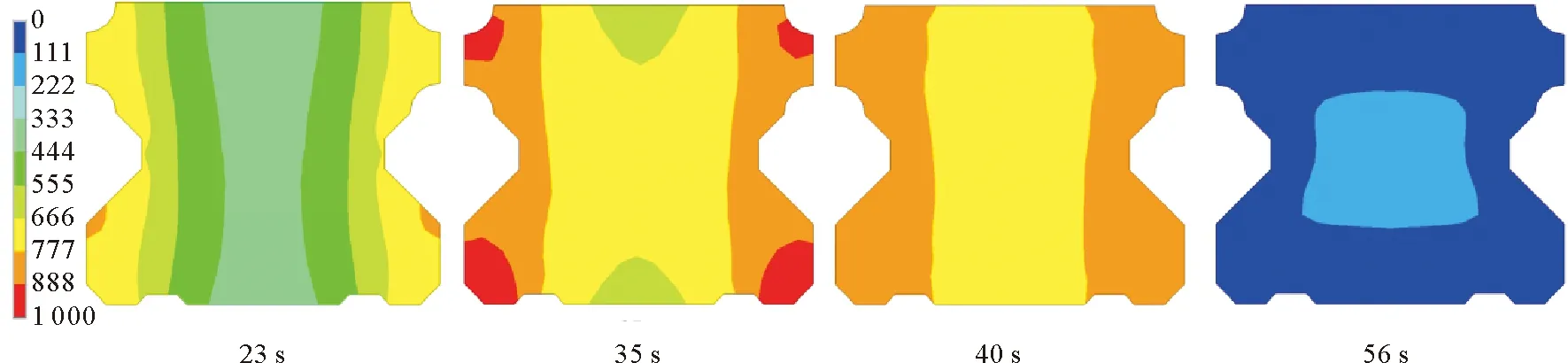
图6 截面在不同时刻的温度分布
2.2 渐进式感应淬火过程的应力场
图7(a)展示了A处表面节点不同方向的热应力变化曲线。20 s时,节点受到了压应力,对比图5(a)可知,由于此时第一感应器到达导轨截面位置,节点温度急剧升高,体积膨胀,对周围尤其是前后的节点造成挤压,周围的节点产生反作用力,所以此节点受压应力,Z方向压应力最大。40 s时,节点温度降低,体积收缩,应承受拉应力。但由于前面喷水器走过的位置表面节点在淬火后内部温度向外传导,后面喷水器还未到达的位置表面节点正在加热,受到前后节点的热膨胀挤压作用,此节点很快又受到了压应力。
图7(b)展示了A处不同深度的节点Z方向热应力曲线。在20 s时,靠近表面的节点由于热膨胀受到前后节点的挤压,产生压应力;而内部节点受到靠近表面的节点拉扯,产生了轻微的拉应力。40 s时,表面节点受到更大的压应力,内部节点也受到更大拉应力。这是因为表面节点虽然冷却收缩,但受到前后节点的挤压作用较大,产生压应力;内部节点冷却收缩,受到Z方向前后节点的挤压作用小,所以表现为拉应力。
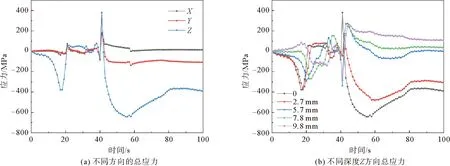
图7 A处的热应力变化
图8(a)展示了A处表面节点不同方向的总应力变化曲线,即热应力、相变应力和相变塑性应力的合成应力变化曲线。对比图7(a)可看出,20 s时节点在Z方向受到的压应力变小了,这是因为节点发生了奥氏体相变,密度变大,体积收缩,于是受到周围节点的牵拉作用,抵消了一部分压应力。40 s时,由于淬火原因,节点发生马氏体相变,密度变小,体积膨胀,与周围节点相互挤压,三个方向都产生了很大的压应力。
图8(b)展示了A处不同深度节点Z方向总应力曲线,可以看出,越靠近表面的节点压应力越大,这是由于表面的节点温度变化比内部大,且靠近表面的节点发生了奥氏体相变和马氏体相变。由于内部节点未发生相变,并且在后期淬火结束后,内部节点热量向外传导,温度下降造成内部节点受到拉应力。
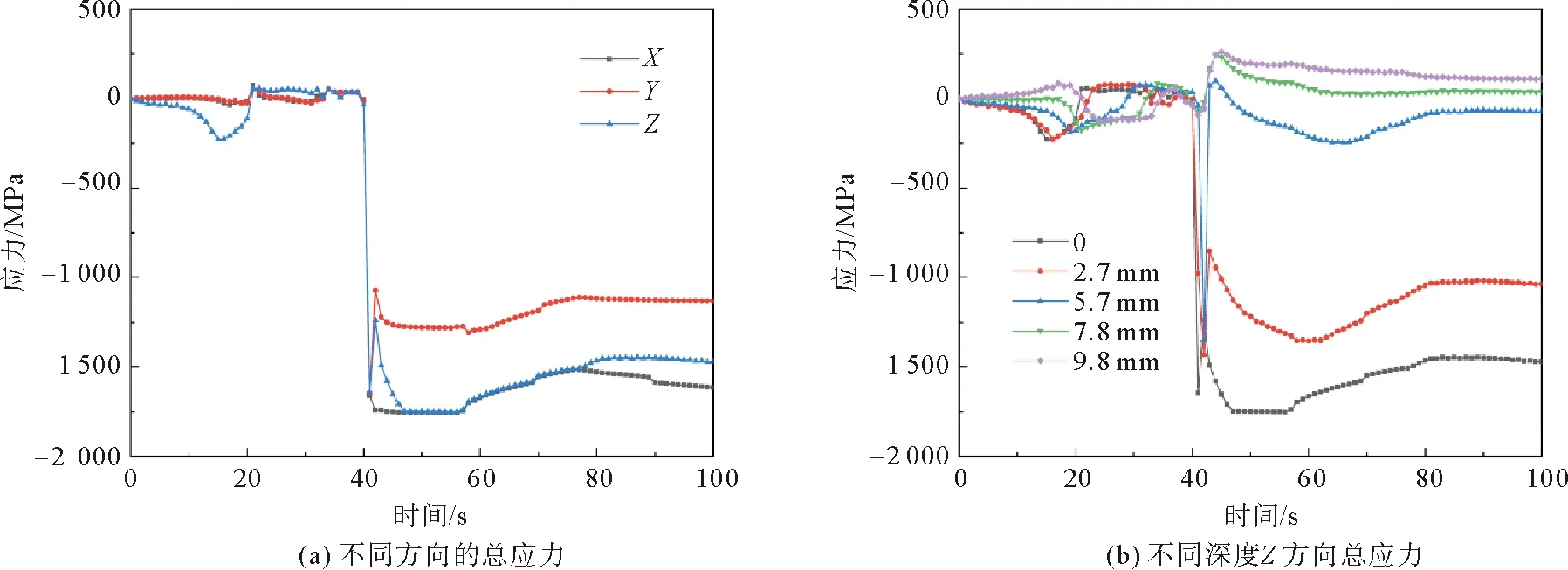
图8 A处的总应力变化
2.3 渐进式感应淬火过程的组织场
图9为导轨截面在感应加热后奥氏体的体积分数,红色区域为完全奥氏体,蓝色区域为铁素体和珠光体基体组织,红色和蓝色之间区域为过渡区。A、B、C三处完全奥氏体化深度分别为5.8、2.1和5.9 mm。
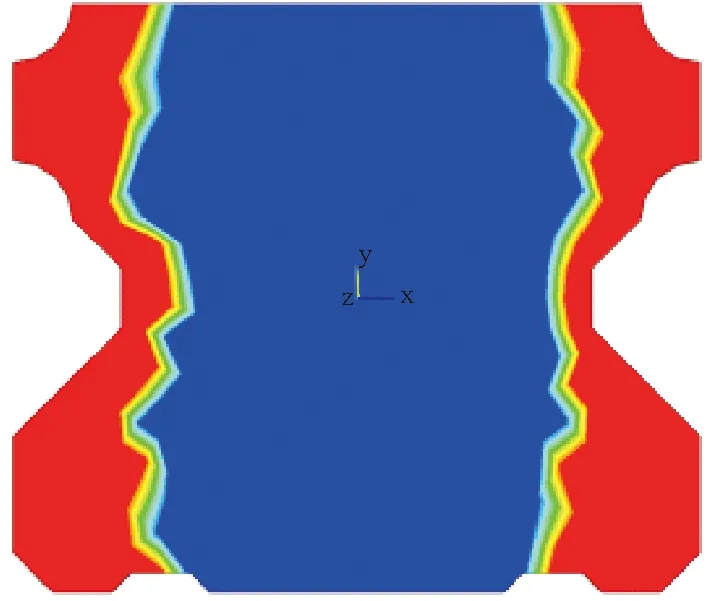
图9 感应加热后奥氏体体积分数分布(模拟结果)
对比模拟的温度结果,可以看出导轨在感应淬火过程中,加热时表面温度较高的部分充分奥氏体化,然后随着淬火组织转变为马氏体;内部温度稍微低一些的部位发生了部分奥氏体化,再往里的部分由于没有达到奥氏体化温度,未发生奥氏体转变。这样的淬火效果使得导轨同时具有耐磨性和韧性。
为了验证模拟结果的可靠性,按照数值模拟时的感应淬火工艺参数,用IGBT智能感应电源对LG35直线导轨进行渐进式感应淬火,然后切下导轨中间一小段经过研磨、抛光、腐蚀后,拍下宏观组织分布和微观组织形貌图。图10为截面微观组织分布的模拟结果和实验结果对比,可以看出,导轨两侧的组织为马氏体,中间为铁素体和珠光体的混合组织;模拟得到的A、B、C三处淬硬层深度分别为5.8、2.1和5.9 mm,实验结果分别为5.3、1.8和5.4 mm;模拟结果和实验结果吻合度较高。
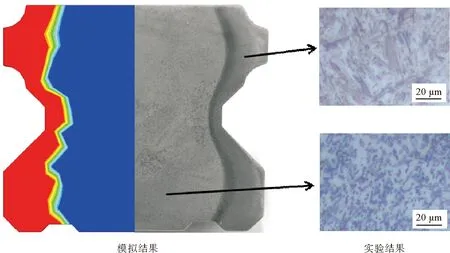
图10 组织分布的模拟结果和实验结果对比图
3 结论
1) 渐进式双感应器对导轨两侧同时加热效果良好,可以保证导轨两侧表面完全奥氏体化,中间部分维持铁素体+珠光体组织。
2) 两个感应器之间的间距可改善导轨表面温度的均匀性,提高导轨表面奥氏体化程度的均匀性,减少导轨的淬火畸变。
3) 考虑相变应力和相变塑性后,奥氏体化过程中总应力比热应力小,但马氏体相变后总应力比热应力大,导轨表面呈现较高的压应力,有利于提高导轨的疲劳寿命。
4) 微观组织模拟结果与实验结果吻合度较高,表明所构建的多物理场耦合模型具有较高的可靠性,可用于直线导轨感应淬火工艺参数的设计和优化。

