利用重心基准的激光跟踪三维测边网平差
刘 硕,刘光博,刘尚国
(1.山东科技大学 测绘与空间信息学院,山东 青岛 266590;2.通用技术集团工程设计有限公司,山东 济南 250031)
在工业测量领域,常面临观测目标尺寸大、精度要求高、测量现场环境复杂等一系列问题,对高精度控制网的构建提出了更高的要求[1-3]。激光跟踪仪采用激光干涉测距,距离测量的精度极高,且测量范围大,自动化程度高,操作简便,已成为目前构建精密三维控制网的重要手段[4-5]。然而,为了保证其动态测量速度的需要,激光跟踪仪测角系统一般采用光栅度盘,很难消除度盘误差对其测角误差的影响[6],而测角误差是影响其点位误差的主要因素[7]。因此,相比于微米级测距精度,激光跟踪仪的测角精度并没有显著提高,鉴于激光跟踪仪的测距精度对空间点位精度起主导作用[8],为消除测角误差的影响,在构建精密三维网时通常仅使用激光跟踪仪的高精度测距结果。而在具体平差计算时,必须解决自由网平差基准秩亏的问题。文献[9]采用混合总体最小二乘迭代算法求解多测站空间坐标转换参数,并分析了测站定位与定向对激光跟踪仪光束法平差的影响。文献[10]则针对激光跟踪三维测边控制网中的秩亏问题,提出利用矩阵奇异值分解性质求解未知参数,实现对激光跟踪仪测角误差的有效约束,方法实用性强且易于编程实现,可解决自由网平差基准秩亏的问题,但在附加重心基准约束及其平差结果校验等方面,尚需开展进一步探讨。
本研究以Leica AT930型激光跟踪仪为研究对象,通过激光跟踪仪多站位测量,构建了高精度三维测边网。利用公共点转换模型,求取激光跟踪仪各测站点在基准坐标系下的近似坐标,再利用测边网平差前后重心位置不变的性质,引入重心基准作为附加约束条件;并利用该性质作为测边网平差后的检核条件,以解决测边网中秩亏自由网平差的问题。
1 激光跟踪三维测边网的构建

第i个测站对第j个全局控制点的激光干涉测距值
(1)
对式(1)进行线性化,可得误差方程式:
vij=aijδXi+bijδYi+cijδZi-aijδxj-bijδyj-cijδzj-lij,
(2)
式中,系数aij、bij、cij与常数lij分别如下所示。
其中,lij表示的是第i个测站与第j个控制点间激光干涉测距值与近似值的差值。
对测量空间内m个测站、n个控制点应用式(1),建立误差方程并写成矩阵形式,则有
Vmn×1=Amn×3(m+n)δX3(m+n)×1-lmn×1。
(3)
式中:V为残差向量,δX为待求未知参数向量,A为系数矩阵,l为距离差值常数向量,分别如下所示。
V=[v11,v12,…,v1n,…,vm1,vm2,…,vmn]T,l=[l11,l12,…,l1n,…,lm1,lm2,…,lmn]T,
δX=[δX1,δY1,δZ1,…,δXm,δYm,δZm,…,δx1,δy1,δz1,…,δxn,δyn,δzn]T,
2 平差前测边网近似三维坐标的解算
在利用重心基准的激光跟踪三维测边网平差中,测站点与全局控制点的近似三维坐标计算是平差处理的首要问题。全局控制点的近似三维坐标,一般取自基准坐标系(假定第1测站坐标系为基准坐标系)下的单测站观测成果。而关于各测站近似坐标的处理,本研究首先考虑利用空间距离后方交会的方法进行解算。如图1所示,假设PA、PB、PC三个控制点在基准坐标系下的坐标已知,PE点为未知点。在PE点处设置激光跟踪仪测站,依次观测PA、PB、PC控制点,获取3个激光干涉测距值D1、D2、D3。
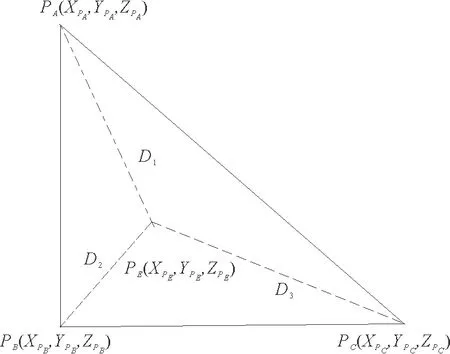
图1 距离后方交会
由空间距离的计算公式,可得
(4)
通过解算上述三元二次方程,即可求得未知测站点PE的三维坐标。但使用后方交会方法获取测站点近似坐标时,解的精确与否与三点交会的网形有很大关系,若网形不佳如PA、PB、PC三点接近共线或共圆,会造成解算结果的失真,影响下一步测边网的平差工作。
因此,考虑利用公共点转换模型求取各测站的近似坐标。即在某测量空间选取不少于3个目标点,并保证所选目标点在每一个测站下都得到了观测。选择某测站坐标系为基准坐标系,将每一测站下所选目标点转换至基准坐标系,求取坐标转换参数,然后导入相应测站坐标,即可求得其在基准坐标系下的坐标。将求得的各测站点近似坐标、基准坐标系下的单测站观测成果作为三维测边网平差前的初始值。
3 基于重心基准的三维测边网平差模型
对式(3)应用最小二乘原理,可得法方程式:
NδX-W=0,
(5)
式中,法方程系数矩阵N=ATPA,常数阵W=ATPl,P为权矩阵,参考文献[11],P可由式(6)确定
Pij=(1/mSSij)2。
(6)
式中mS为仪器出厂时的标称测距精度。
在激光跟踪三维测边控制网中,所有测站点、控制点三维坐标作为未知参数参与平差,且基于激光干涉测距值构建的激光跟踪三维测边网,仅有尺度基准而缺少位置、方位基准,因此该三维测边网的平差解算属于典型的秩亏自由网平差问题[12]。系数矩阵A为秩亏矩阵,因此法方程系数矩阵N为奇异矩阵,式(5)的解不唯一。为了获得唯一解,需加入新的约束条件。依据秩亏网平差原理,三维控制网中重心位置是固定不变的。因此,可利用重心基准条件进行约束,其平差模型为:
GTδX=0,
(7)
式中G为附加约束矩阵。激光跟踪三维测边网的基准数为6[13],因此,该附加约束矩阵为:
由式(7)可得到:
(8)
(9)
联立式(8)与式(9)可得平差后重心坐标为:
(10)
从式(10)可以看出,平差后测站点与全局控制点重心坐标等于平差前各点的重心坐标,该特性可作为基于重心基准的激光跟踪三维测边网平差后的检核条件。
由秩亏自由网平差公式,可分别得到未知参数δX及其协因数矩阵QδXδX:
δX=(N+GGT)-1ATPl,
(11)
QδXδX=(N+GGT)-1N(N+GGT)-1。
(12)
单位权中误差μ和未知参数精度mδX分别为:
(13)
(14)
4 实验与算例分析
4.1 实验测试方案
如图2所示,在山东科技大学3D试验场内,选取约10 m×10 m的测量范围,均匀布设7个全局控制点,编号为Ph(h=1,2,…,7),其中P1、P2、P4、P5位于地面上,P3、P6、P7位于墙面上,点间最大高差约为0.9 m。
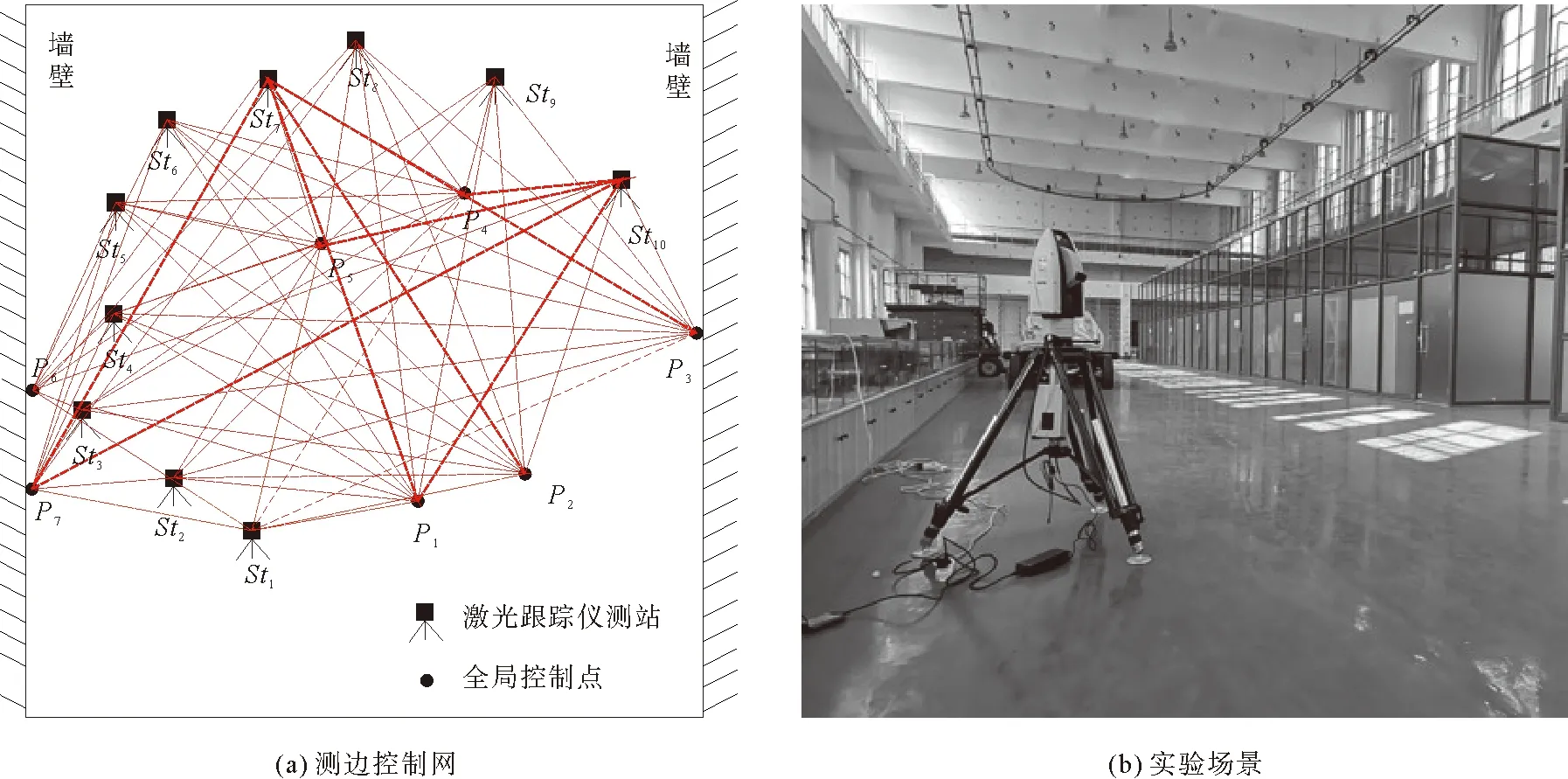
图2 测边控制网及实验场景
采用Leica AT930型激光跟踪仪作为测量设备,共设置10个测站,编号依次为Stk(k=1,2,…,10),依次观测7个全局控制点。观测前用热熔胶固定控制点基座,将球棱镜放置于基座上并调整好激光入射角度即可进行观测。
4.2 三维坐标初始值的计算
假设各测站点坐标为(0,0,0),选择St1测站坐标系作为基准坐标系,利用公共点转换模型,求取其他各测站点在St1测站下的坐标值,将其作为激光跟踪三维测边网平差前的初始值,各测站点坐标初值与全局控制点坐标初值如表1所示。
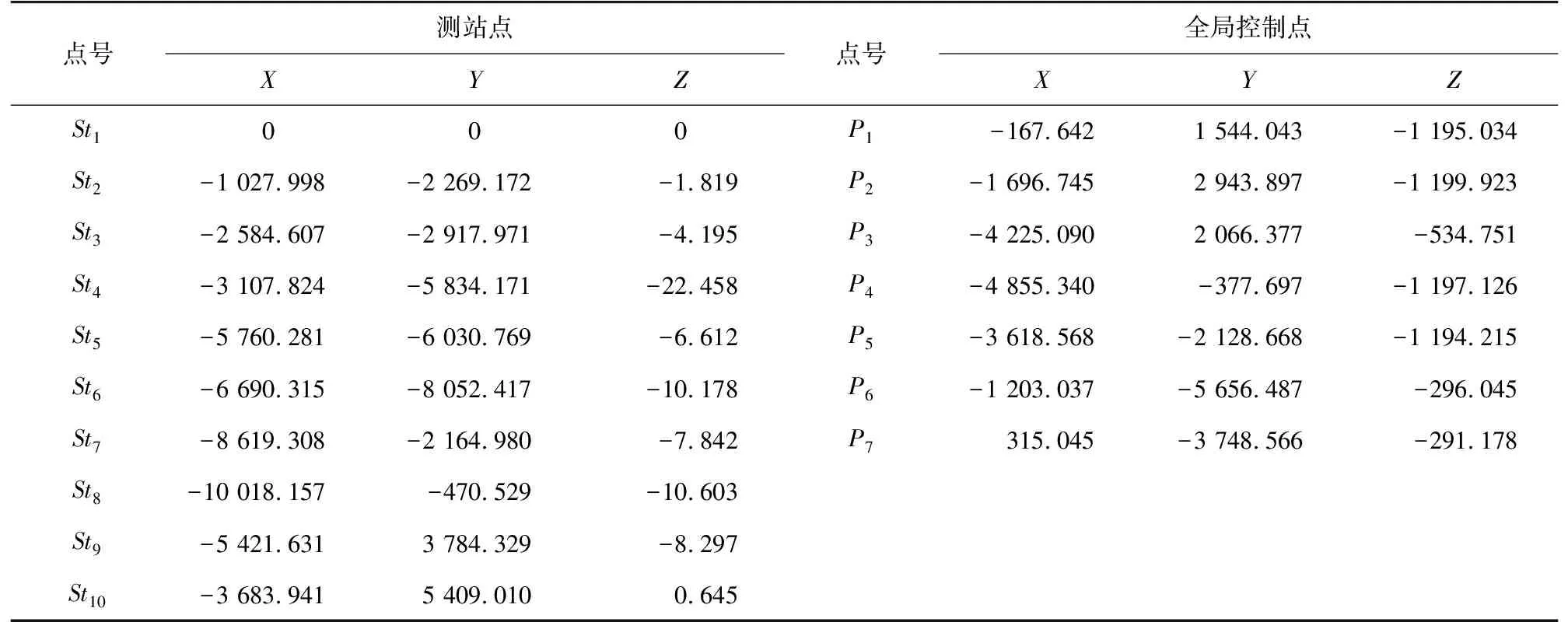
表1 测站点与全局控制点坐标初值
4.3 重心基准约束下的算法及程序设计
该激光跟踪三维测边网中,有70个观测方程,51个未知参数,6个基准数,25个多余观测数,误差方程有解。通过软件编程,实现了附加重心基准约束条件的秩亏自由网平差解算(图3)。算法流程如图4所示,导入测站点、控制点坐标初值,并将激光干涉测距值作为真实值参与平差。计算平差前测边网的重心坐标O1与平差后的重心坐标O2,用以检验该测边网平差后的准确性。平差后,单位权中误差为5 μm,平差结果与各未知参数精度如表2、表3所示。

图3 平差模型解算界面Fig. 3 Solution interface of adjustment model

图4 三维测边网平差算法流程图
由表2、表3测站点与全局控制点平差结果,可以反算各测站到全局控制点的距离,其与激光干涉测距值的差值可用以检验平差结果的准确性。图5表示平差前与平差后各点坐标反算距离与激光干涉测距值的差值。
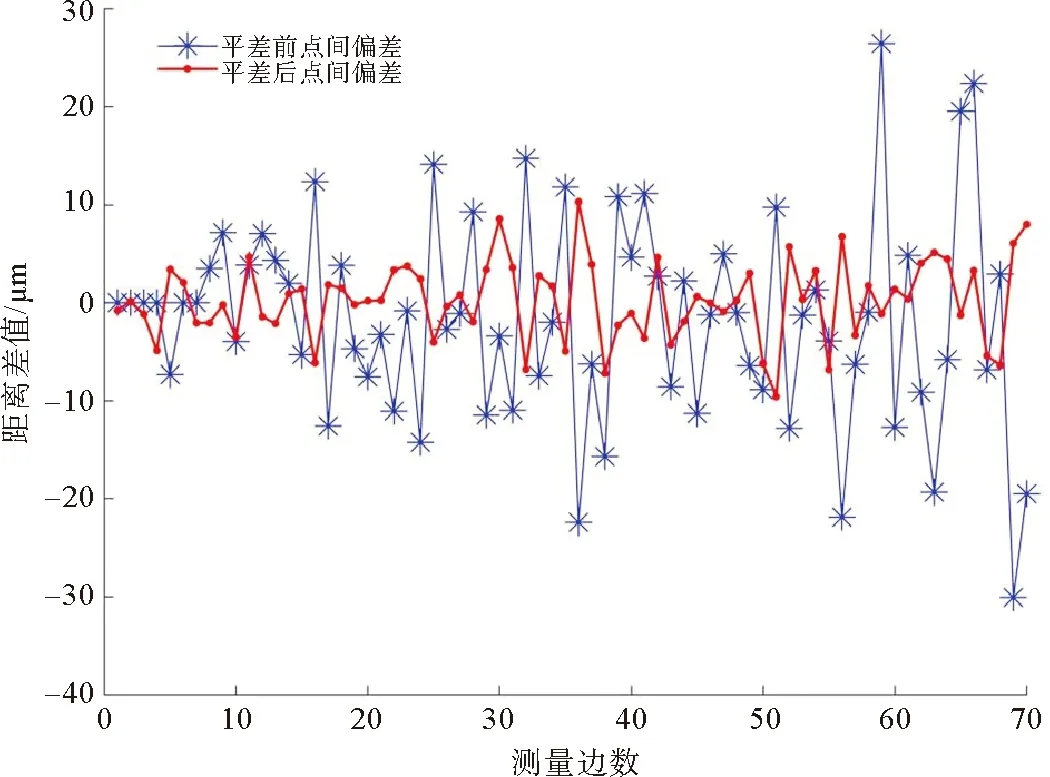
图5 平差前后坐标反算距离与激光干涉测距值的差值
4.4 实验分析
1) 对表2、表3依据重心公式计算可得,平差前该控制网重心坐标O1等于平差后点坐标计算的重心坐标O2,验证了激光跟踪三维测边网平差前后,网重心位置不变的性质。

表2 测站点坐标平差结果
2) 测站点与全局控制点平差后,平面精度平均值约为14 μm,而高程精度平均值为62 μm,即平差后点的高程精度略差于平面精度。
3) 由表3可以看出,地面控制点精度平均值为43 μm,墙面控制点精度平均值为115 μm,即地面点精度优于墙面点精度,分析原因是部分布设在墙面上的点位稳定性较差,对最终点位测量精度产生了较大影响。
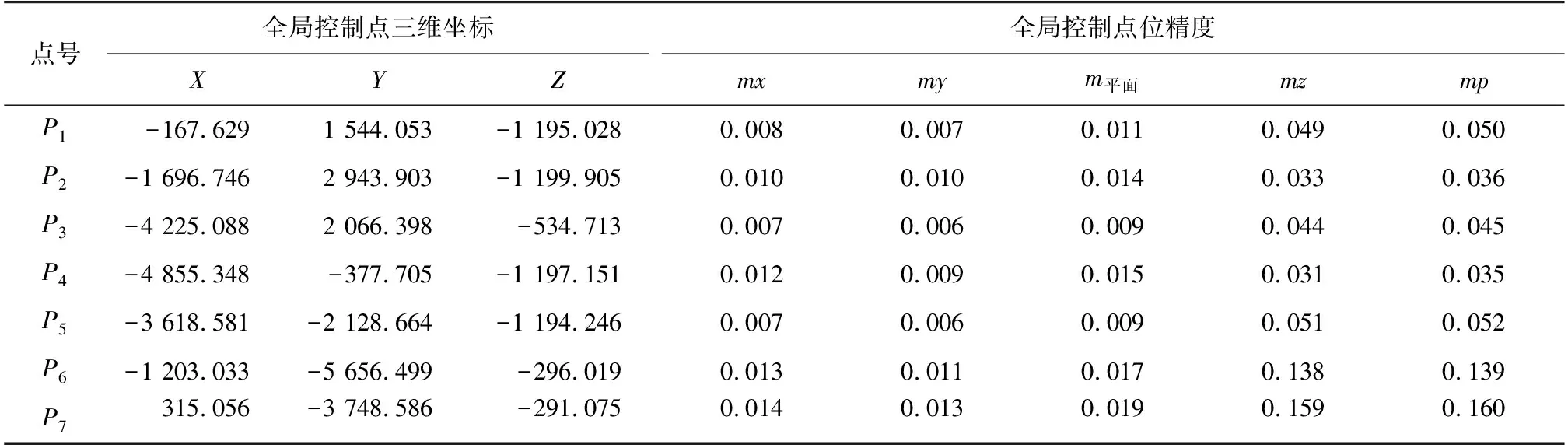
表3 全局控制点坐标平差结果
4) 经平差处理后,激光跟踪仪测站点位误差最大值为79 μm,最小值为42 μm,平均值为57 μm;而全局控制点点位误差最大值为160 μm,最小值为35 μm,平均值为74 μm,即测站点精度略高于控制点精度。
5) 由图5可以看出,利用重心基准的激光跟踪三维测边网平差后,点坐标反算距离与激光干涉测距值的差值较平差前更为均匀。平差前该差值最大为26.5 μm,最小为-30.1 μm,平均值为-1.8 μm;平差后该差值最大为10.3 μm,最小为-9.6 μm,平均值仅为0.2 μm,证明该平差模型可对激光跟踪仪测角误差进行有效的约束。
5 结论
本研究利用激光跟踪仪微米级测距精度的优势,在试验场内构建了高精度三维测边网,基于控制网平差前后重心基准不变的性质,较好地解决了三维测边网中秩亏自由网平差的问题。实验表明,利用重心基准的激光跟踪三维测边网平差模型,可有效地消除激光跟踪仪测角误差对整体测量精度的影响,在10 m×10 m测量范围内,平差后的测站、控制点点位精度平均值优于0.1 mm。平差后,点坐标反算距离与激光干涉测距值的差值可控制在10 μm以内。

