一类二阶半线性微分方程的振动性

罗红英，俞元洪

(1.曲靖师范学院 数学与统计学院，云南 曲靖 655011；2.中国科学院 数学与系统科学研究院，北京 100190)

1 引言

微分方程有着悠久的历史。随着科学技术的发展，微分方程理论在自然科学和社会科学领域均具有广泛的应用。对于微分方程的振动性而言，若其解是振荡的，则方程的解就是振动的。近年来，微分方程振动性理论作为微分方程定性理论的重要内容之一，受到人们的普遍关注，其发展相当迅速，从线性到非线性，从低阶到高阶，从分散到连续，都有一些新的研究成果。因此，对其进行研究不仅具有重要的理论意义，也具有重要的实际应用价值。文献[1]研究了二阶微分方程

(r(t)(z′(t))α)′+q(t)f(x(σ(t)))=0

文献[2]研究了n阶微分方程

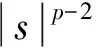
文献[3]研究了二阶微分方程

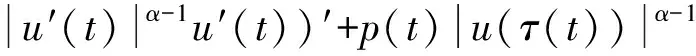
的振动性。

文献[4-6]研究了二阶微分方程的振动性，但文献[1-6]都只考虑了微分方程中两项的次数相等(即α=β)的情形，是按照常规的Riccati变换方法得到微分方程振动的充分条件。文献[7-16]也研究α=β的情况，将所作的二阶方程Riccati变换推广到相应的三阶微分方程，得到了三阶微分方程振动的充分条件。但由于文献[1-6]研究二阶方程时是对α=β情形进行了研究，因此，在将二阶微分方程的Riccati变换推广到三阶微分方程时,只能针对三阶微分方程α=β的情形进行了研究[7-16]。可是，振动性问题不能仅仅只研究α=β的特殊情形，对于α>β和β≥α的情形，如果还采用常规的Riccati变换方法就不行了。文献[17]在改进了文献[1-16]所作的常规Riccati变换技巧后，得到了方程

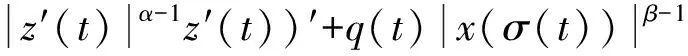
在α≥β>0情形振动的充分条件。文献[18]对文献[17]中采用的Riccati变换和积分平均技巧作进一步的推广，对文献[17]研究的方程在两种情况下得到了该方程振动的充分条件，推广和改进了文献[17]的方法和结论。

在文献[18]的基础上，研究如下的带积分项的二阶半线性中立型微分方程：

(1)

为了能对α>β和β≥α两种情况都能进行研究，我们推广文献[18]的Riccati变换和积分平均技巧，利用推广的广义Riccati变换和积分平均技巧，得到方程(1)振动的充分条件。

H1)r(t)∈C1([t0,∞),R+),r′(t)≥0，r(t)>0；

σ(t,ξ)关于变量ξ是减函数；

2 主要结论

针对方程(1)中出现的α和β的情形，对α>β和β≥α两种情况研究方程(1)的振动，在文献[18]的基础上，应用推广的Riccati变换和积分平均技巧，得到方程(1)在α>β和β≥α两种情况下振动的充分条件。

定理1设

(2)

且存在ρ(t)∈C1([t0,∞),R+)，使得

(3)

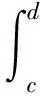
证明：用反证法。假设方程(1)有非振动解x(t)，不妨设x(t)>0，由方程(1)，有

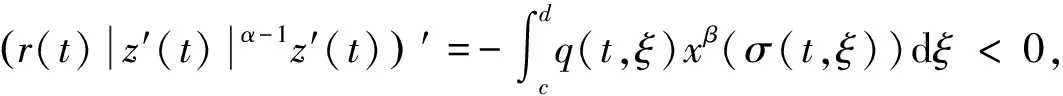
断言z′(t)>0。否则z′(t)<0，有

(r(t)(-z′(t))α)′>0。

即r(t)(-z′(t))α是增函数，则存在T>0，对∀t>T，有

r(t)(-z′(t))α≥r(T)(-z′(T))α=k1，

其中k1=r(T)(-z′(T))α，则

将上式在[T,t]上积分，得

上式与式(2)矛盾，因此，z′(t)>0。

由z(t)的定义，z(t)≥x(t)，则z(τ(t,ξ))≥x(τ(t,ξ))，而z′(t)>0，z(t)是增函数，z(τ(t,ξ))≤z(t)，故

即

x(t)≥z(t)[1-p(t)]，x(σ(t,ξ))≥z(σ(t,ξ))[1-p(σ(t,ξ))]。

而σ(t,ξ)关于变量ξ是减函数，有σ(t,ξ)≥σ(t,d)，故z(σ(t,ξ))≥z(σ(t,d))，则

x(σ(t,ξ))≥z(σ(t,d))[1-p(σ(t,ξ))]。

则

由式(1),得

(r(t)(z′(t))α)′+Q(t)zβ(σ1(t))≤0。

(4)

定义函数

则

1) 若β≥α，则

则

由条件H1)和H3)，r(σ1(t))≤r(t)，因此，有

(5)

2) 若α>β，则

由于(r(t)(z′(t))α)′≤0，得z″(t)≤0，故z′(t)是减函数，有z′(σ1(t))≥z′(t)，则

又z′(t)是减函数，则对∀t>T，有

则

(6)

综上所述，令λ=min{α,β}，k=min{βk2,βk3}，则式(5)与式(6)合并写成

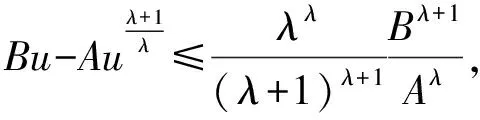
在[T,∞)上积分，得

此式与式(3)矛盾，则方程(1)振动。

推论1若存在函数ρ(t)∈C1([t0,∞),R+)，使得

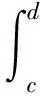
证明：易验证满足定理1条件。

推论2设式(2)成立，若存在ρ(t)∈C1([t0,∞),R+)，使得

(7)

(8)

成立，则方程(1)振动。

证明:由式(8)知，存在ε0>0和t1>t0，使得对t>t1，有

则

即

在[t1,t]上积分，得

由式(7)知满足定理1条件，则方程(1)振动。

定理2设式(2)成立，且

(9)

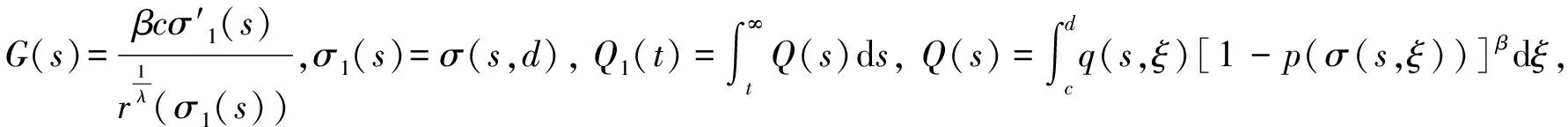
证明：定义函数

则

1) 若β≥α，则

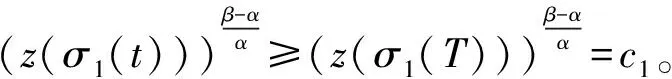
即

则

(10)

2) 若α>β，则

而(r(t)(z′(t))α)′≤0，得到z″(t)≤0，z′(t)是减函数，有

z′(σ1(t))≥z′(t)。

又z′(t)是减函数，则对∀t>T，有

则

(11)

综上所述，令λ=min{α,β}，c=min{c1,c2}，则式(9)与式(10)合并写成

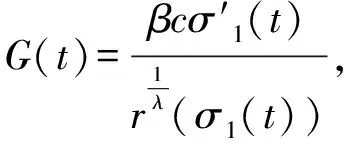
(12)

将式(12)在[t,∞)上积分，得

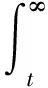
即

(13)

(14)

即

则

(15)

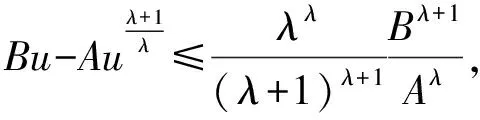
上式与式(15)矛盾，因此，方程(1)振动。

注：定理1中的ρ(t)∈C1([t0,∞),R+)需要根据具体的微分方程去构造，而定理2没有这个限制条件，定理2是定理1的补充。定理1是文献[18]中定理2.1的推广，定理2是文献[18]中定理3.2的推广。

为了说明所得主要结果的适用性，现通过例题来验证其结论。

例考虑下列二阶微分方程

(16)

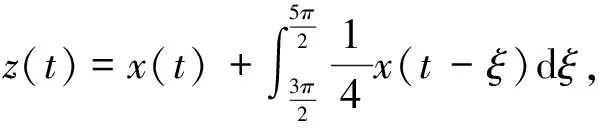
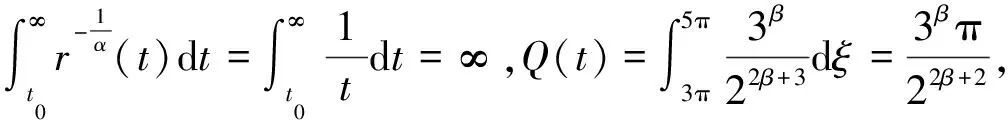
故满足定理1条件，方程(16)振动。

本研究在文献[1-18]对二阶和三阶微分方程振动性研究的基础上，利用推广的广义Riccati变换和积分平均技巧，研究了一类二阶半线性中立型微分方程(1)，得到了其振动的充分条件，并给出例子说明所得结论的适用性。今后将Riccati变换和积分平均技巧应用到更广泛的非线性微分方程模型中。