SPSS进行面板数据分析的基本方法

○ 文/李国柱 李子宁 李从欣

文章梳理了面板数据尤其是短面板数据的估计方法，提出了用SPSS软件进行了混合回归、组间估计、组内估计、一阶差分估计、最小二乘虚拟变量估计的操作流程，并与STATA软件的估计结果进行了对比。结果证实，用SPSS估计面板数据可以得到与STATA完全相同的结果，拓展了SPSS软件的使用范围。

SPSS是世界上应用最广泛的统计软件之一，其特点是操作简单、统计方法比较齐全，在视窗版软件中得到广大用户的认可。但SPSS软件也有一个大的缺点，其包括的统计方法主要是基于截面数据的统计方法，在时间序列数据方面仅包括自相关图、互相关图、专家建模器等，没有单位根检验、协整分析、向量自回归模型等估计方法，而对于面板数据更是丝毫没有涉及。面板数据由于可以解决遗漏变量问题、提供更多动态行为信息以及使样本容量增大，在实证研究中得到越来越广泛的应用。那么能否用SPSS进行面板数据分析呢？虽然不能直接估计，但只要熟知面板数据的估计方法，通过适当的操作，SPSS也可以估计面板数据。

一、SPSS输入面板数据的方法

SPSS默认输入的是截面数据，当输入时间序列数据时，必须首先通过“数据/定义日期”过程定义时间变量，然后通过“转换/创建时间序列”功能创建一个新的时间序列。而对于面板数据，可采用类似STATA软件的输入方式，除包括建模的变量外，还需要创建一个日期变量和截面变量。本文以2010-2017年我国31个省（自治区、直辖市）的数据为例，说明面板数据的输入方法以及各种估计方法。

SPSS面板数据输入格式

假定要分析投资对国内生产总值的影响，需要在SPSS中新建四个变量，其中province代表不同的省份（即截面单元），year代表年份（即时间单元），gdp代表国内生产总值，invest代表投资。上图是与STATA软件相同的输入格式。

当然，也可以把上图中的数据格式按变量year进行排序，此时数据中前31行为2010年各省份的数据，32-62行是2011年各省份的数据，以此类推。面板数据的两种排列方式并不影响分析结果。

二、混合回归模型的参数估计

如果从时间上看，不同个体之间不存在显著差异，从截面上看，不同个体之间也不存在显著差异，这种模型与一般回归模型无本质差异，只要满足经典回归基本假定条件，就可以把所有数据放在一起进行混合最小二乘估计，估计量具有线性、无偏和有效性。

SPSS进行混合回归很简单，在菜单中依次选择“分析/回归/线性回归”，在弹出的对话框中，因变量选择gdp，解释变量选择invest，其他选择默认设置，点“确定”按钮即可得到混合回归结果，汇总如表1所示。

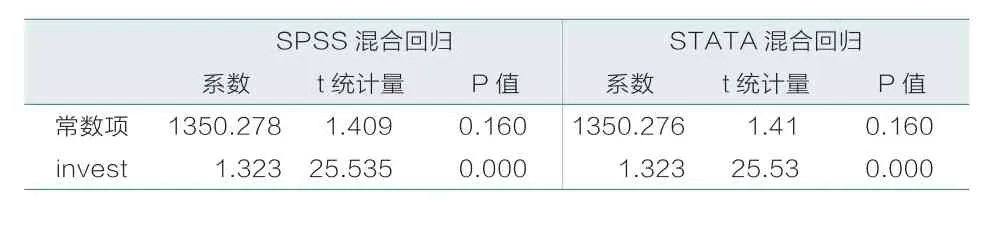
表1 SPSS与STATA混合回归结果

由表1可以看出，SPSS混合回归结果和STATA混合回归结果相同，解释变量invest的系数均为1.323，t统计量值均为25.535，p值均为0。

三、固定效应模型的参数估计

面板数据模型可表示为：

其中，yit是被解释变量，xit是随个体和时间而变化的解释变量，zi是不随时间而变的个体特征；不可观测的随机变量αi代表个体异质性，随个体变化，但不随时间变化，即个体效应；β是回归系数，对于不同个体回归系数β是相同的；uit是随机误差项。在以后的实证分析中，将用具体变量名代替yit和xit。

若αi与某个解释变量相关，则称为固定效应模型；若αi与xit和zi均不相关，则称为随机效应模型。因此固定效应模型和随机效应模型在表达式上是相同的，都是模型（1），只是根据个体效应与解释变量是否相关区分为固定效应模型和随机效应模型。

（一）组内估计量

对于固定效应模型，由于αi与某个解释变量相关，故OLS不是一致的估计。解决方法之一是对面板数据中每个个体的观测值针对时间求其平均值，利用离差变换消掉个体效应αi，采用OLS方法估计模型回归系数β。

给定个i体，将模型（1）两边对时间求平均可得：

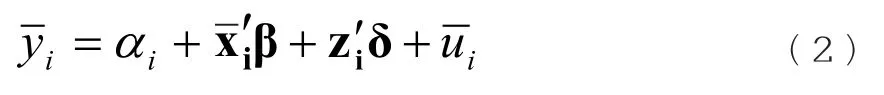
将模型（1）减模型（2）可得：

在采用SPSS计算组内估计量时，共需要三个步骤。第一步要计算每个地区的均值，在菜单中依次选择“数据/分类汇总”，在弹出的对话框中，将provicne选入“分组变量”复选框，将gdp和invest选入“汇总变量”复选框。点击“确定”按钮后，SPSS数据窗口增加了两个均值变量，均值变量名SPSS默认为gdp_mean和invest_mean。第二步在菜单中依次选择“转换/计算变量”，在弹出的对话框中将目标变量定义为gdpstar，数学表达式定义为“gdp-gdp_mean”，点击“确定”后可得到中心化后的因变量值；按类似的方法可得到invest中心化后的变量investstar。第三步在菜单中依次选择“分析/回归/线性回归”，在弹出的对话框中，因变量选择gdpstar，解释变量选择investstar，其他选择默认设置，点“确定”按钮即可得到组内估计量结果，汇总如表2所示。

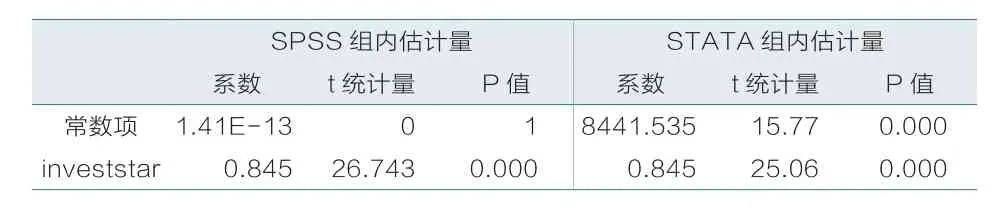
表2 SPSS与STATA组内估计量

由表2可知，SPSS计算的组内估计量中，解释变量的系数为0.845，t统计量值为26.743，p值为0；STATA计算的组内估计量中，解释变量的系数为0.845，t统计量值为25.06，p值为0；除了t统计量值稍有差异外，系数估计值与p值完全相同。需要注意的是，两种软件对常数项的估计并不相同，原因在于两种软件对常数项的定义不同。在用SPSS进行组内估计时，由于采用按时间平均然后中心化，个体效应已经被消掉了，也就是组内回归没有常数项，这也是SPSS组内估计结果常数项的p值为1的原因。而STATA结果中的常数项实际上是个体效应的均值，即，各个地区的个体效应为，根据离差和恒等于零的性质，个体效应之和等于零，因此STATA结果和SPSS结果并不矛盾。

（二）一阶差分估计量

削掉个体效应的另外一种方法是一阶差分法。对于模型（1），取其滞后一期的关系式，得

将模型（1）减模型（4）可得：

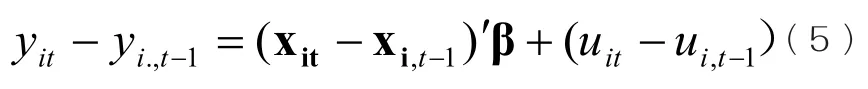
SPSS只有定义时间序列变量后才能产生滞后变量和差分变量，而对于面板数据，SPSS很难直接产生滞后变量和差分变量，可以借助STATA软件产生差分变量，然后复制到SPSS软件中，当然也可以采用EXCEL，只不过稍微繁琐一点。令gdp差分后的变量为dgdp，invest差分后的变量为dinvest。在菜单中依次选择“分析/回归/线性回归”，在弹出的对话框中，因变量选择dgdp，解释变量选择dinvest，然后点击“选项”按钮，将“包含常数项”前面的对钩去掉，表示模型不包含常数项；其他选择默认设置，点“确定”按钮即可得到一阶差分估计量结果，汇总如表3所示。

表3 SPSS与STATA一阶差分估计量

由表3可以看出，SPSS与STATA一阶差分估计结果完全相同。应当注意的是此处STATA软件估计采用的是因变量差分对解释变量差分直接回归的方法，如果采用xtserial命令，系数估计值和SPSS方法完全相同，但由于该命令采用了稳健标准误，计算出来的t统计量值会有所不同。

（三）最小二乘虚拟变量回归

对于固定效应模型（1）中的个体固定效应αi，将其视为个体i的截矩项，即个体i的待估参数。对于n位个体的n个不同的截矩项，可以通过在模型 （1）中引入n-1个虚拟变量来估计截矩项，估计模型如下：

常数项α1表示被遗漏的虚拟变量D1所对应个体1的截矩项，而个体i（i>1)的截矩项是α1+αi。

对模型（6）采用OLS方法估计，称为“最小二乘虚拟变量法”。如果模型是正确设定的，且符合模型全部假定条件。则回归系数估计量是无偏的、有效的、一致的估计。

在SPSS主菜单中选择“转换/创建虚拟变量”，在弹出的“创建虚拟变量”对话框中，在“针对下列变量创建虚拟变量”框下选入变量province，在“主效应虚拟变量-根名称”下输入“D”，表示虚拟变量，变量名以D开头，点击“确定”按钮后，在SPSS中变量窗口即会出现31个虚拟变量。虚拟变量名和数据中省份的输入顺序有关，上海对应的虚拟变量为D_1，云南对应的虚拟变量为D_2，以此类推。在采用虚拟变量回归时，如果回归方程包括常数项，为了避免“虚拟变量陷阱”，31个省份只能加入30个虚拟变量。STATA默认将数据集中的第一个省份（本例为上海）作为比较的基础，因此为了和STATA估计结果进行比较，在使用SPSS进行最小二乘虚拟变量回归时，不包括虚拟变量D_1。在菜单中依次选择“分析/回归/线性回归”，在弹出的对话框中，因变量选择gdp，解释变量依次选择invest以及D_2-D_31，其他选择默认设置，点“确定”按钮即可得到最小二乘虚拟变量回归结果（如表4）。

表4 SPSS与STATA最小二乘虚拟变量回归

由表4可以看出，除个别系数因计算精度和四舍五入原因稍有差异外，SPSS最小二乘虚拟变量回归结果和STATA结果完全相同。表中的常数项18243.87代表上海市的截距，其他省份对应的系数代表与上海的差距，如云南对应的系数-1578.25代表云南比上海低1578.25。由表中p值可知只有浙江和上海没有显著性差异，江苏、广东、山东显著高于上海。另外，最小二乘虚拟变量回归在解释变量invest的估计上和组内估计量相同，均为0.845。

四、随机效应模型的参数估计

随机效应模型的参数估计方法包括广义最小二乘法和组间估计法。虽然广义最小二乘法最小效，但该方法涉及复杂的矩阵运算和较多参数估计，使用SPSS比较繁琐，此处仅介绍组间估计方法。

对于模型（1），如果对每个个体取时间平均值，得如下模型：

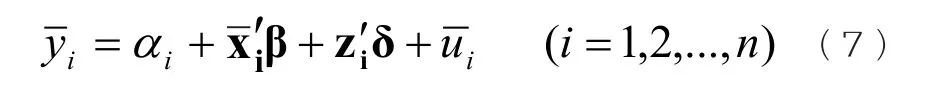
对模型（7）使用OLS进行参数估计，得到的估计量称为组间估计量,记为。由于包含了xit的信息，如果αi与解释变量｛xit，zi｝相关，则不一致。因此不能在固定效应模型下使用组间估计法。组间估计法相当于面板数据被压缩为截面数据。

在采用组内估计量时，已经通过“分类汇总”功能得到各省在gdp和invest两个变量上的均值gdp_mean和invest_mean，但我们并不能采用这两个变量直接回归，原因在于每个省的均值都有8个相同的值（从2010年至2018年），可以采用等距抽样的方法使每个省只有一个均值。为了避免观测顺序打乱，首先在数据集增加一个编号变量（ID），打开需要添加ID号的数据集，选择“文件/新建/语法”，打开弹出的“语法”窗口，并输入以下语句：

DATASET ACTIVATE 数据集名.

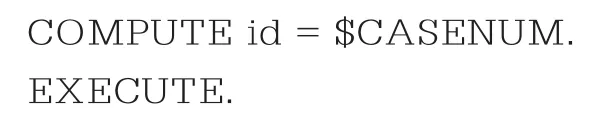
点执行按钮。返回到原先的数据集窗口，则可以看到id号变量了。点击“转换/计算变量”，弹出计算变量对话框，在“目标变量”的空白框中输入新变量名newid，在“函数组”选项框中点击all，在“函数和特殊变量”选项框中点击mod，把mod送入“数字表达式”空白框中，把mod（?,?）的第一个问号改为id-4（由于前8个数值相同，用id减去1-8中的任意一个数均不会影响最终结果），第二个问号改为8。点击“确定”按钮，数据集中newid为0的即是要抽选的样本单元。

选择“数据/选择个案”，打开选择个案对话框，选择第二项“如果条件满足”，单击“如果”按钮后弹出If对话框，将其中的条件设置为“newid=0”，即可得到等距抽样的所有样本，该样本即为进行组间估计的样本。在该样本范围内依次选择“分析/回归/线性回归”，在弹出的对话框中，因变量选择gdp_mean，解释变量选择invest_mean，其他选择默认设置，点“确定”按钮即可得到组间估计回归结果，汇总如表5所示。

表5 SPSS与STATA组间估计量

从表5可以看出，SPSS与STATA估计组间估计量的结果相同。

五、结论与启示

从实证研究结果来看，在混合回归、组内估计、组间估计、一阶差分估计、最小二乘虚拟变量回归方面，SPSS可以得到与STATA软件相同的结果。只不过STATA等软件有内嵌的命令，操作起来很简单，而SPSS由于没有内嵌选项，操作起来相对复杂而已。实际上只要理解各种统计方法的基本原理，以及熟悉SPSS的基本操作，就可以使用SPSS解决大多数没有内嵌的统计方法。