从高考真题看正弦、余弦定理的应用

■江西省赣州市第三中学 叶庆华

大家知道，正弦、余弦定理的主要功能就是解三角形。利用正弦、余弦定理可以求出三角形的边，也可以求角，这类问题既可能出现在选择题或填空题中，也可能出现在解答题中。下面我们来通过几道2021 年的高考真题，来赏析它在解题中的应用。

一、正弦定理的应用

例1（2021 年 高考全国甲卷）2020 年12月8 日，中国和尼泊尔联合公布珠穆朗玛峰最新高程为8848.86（单位：m），三角高程测量法是珠峰高程测量方法之一。图1是三角高程测量法的一个示意图，现有A，B，C三点，且A，B，C在同一水平面上的投影A′，B′，C′满足∠A′C′B′＝45°，∠A′B′C′＝60。。由C点测得B点的仰角为15°，BB′与CC′的差为100，由B点测得A点的仰角为45°，则A，C两点到水平面A′B′C′的高度差AA′－CC′约为（ ）。

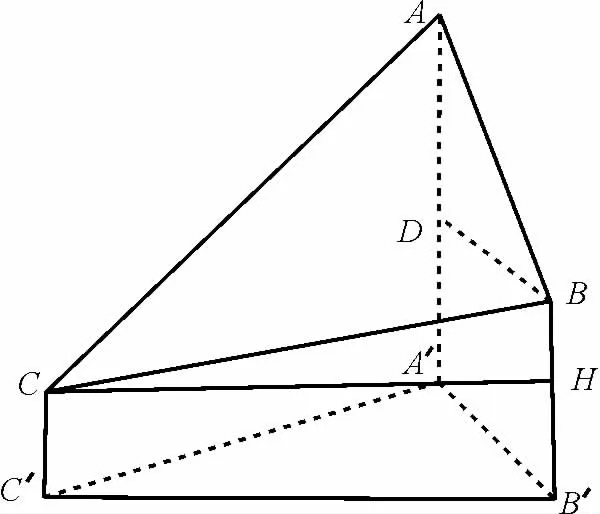
图1

A.346 B.373 C.446 D.473

分析：通过做辅助线，将已知所求量转化到一个三角形中，借助正弦定理，求得A′B′，进而得到答案。

解：过点C作CH⊥BB′，过点B作BD⊥AA′，故AA′－CC′＝AA′－（BB′－BH）＝AA′－BB′＋100＝AD＋100。

由题易知△ADB为等腰直角三角形，所以AD＝DB。

因此，AA′－CC′＝DB＋100＝A′B′＋100。

点评：本题考查解三角形的实际应用。解答的关键在于如何正确将AA′－CC′的长度通过作辅助线的方式转化为A′B′＋100，然后利用正弦定理求解。本题是立体几何背景下的解三角形问题，体现了高考命题一题多考的原则。

二、余弦定理的应用

例2（2021年高考浙江卷）在△ABC中，∠B＝60°，AB＝2，M是BC的中点，AM＝2，则AC＝____，cos∠MAC＝____。

分析：由题意结合余弦定理可得BC＝8，进而可得AC，再由余弦定理可得cos∠MAC。

解：由题意作出图形，如图2所示。

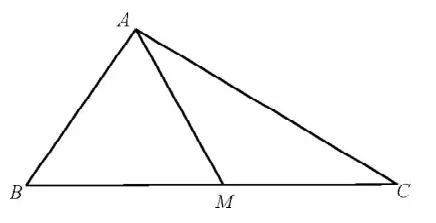
图2

在△ABM中，由余弦定理得AM2＝AB2＋BM2－2BM·BA·cos60。。

代入数据得12＝4＋BM2－2BM×2×，解得BM＝4或－2（舍去）。

所以BC＝2BM＝2CM＝8。

在△ABC中，由余弦定理得AC2＝AB2＋BC2－2AB·BC·cos60。＝4＋64－2×2×8×＝52。

点评：本题的解答过程中三次应用了余弦定理。余弦定理在解三角形中一般有三个应用：（1）已知两边及其夹角，求第三边；（2）已知三边求任何内角的余弦值；（3）已知两边以及一边的对角，可以把第三边当成未知数，利用余弦定理列方程，通过解方程来求第三边。

三、正弦、余弦定理的综合应用

例3（2021年新高考全国Ⅰ卷）如图3，记△ABC中内角A，B，C的对边分别为a，b，c。已知b2＝ac，点D在边AC上，BDsin∠ABC＝asinC。

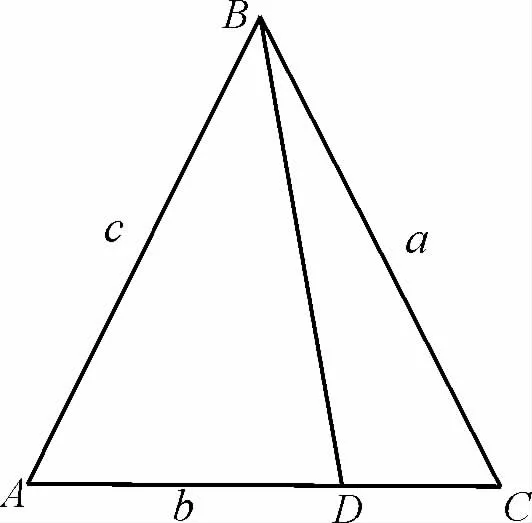
图3

（1）证明：BD＝b；

（2）若AD＝2DC，求cos∠ABC。

分析：（1）根据正弦定理的边角关系得到BD＝，结合已知条件即可证结论。

点评：有关解三角形的题目时，要有意识地考虑用哪个定理更合适，或是两个定理都要用，要抓住能够利用某个定理的信息。一般地，如果式子中含有角的余弦或边的二次式时，要考虑用余弦定理；如果式子中含有角的正弦或边的一次式时，则考虑用正弦定理；以上特征都不明显时，则要考虑两个定理都有可能用到。