数列中的“新定义”问题

■河南省许昌高级中学 胡银伟

近年高考数列的命题中常出现“新定义”问题，先给出定义的新概念、新公式、新法则、新符号、新运算，然后据此新定义去解决问题。解答此类“新定义”问题，需认真研读题意，分析、理解新定义、新情景的特征，能够透过现象看到“新”的本质，以不变应万变是解答此类问题的法宝。

类型一 定义新概念

例1（2020年新课标Ⅱ卷）0－1周期序列在通信技术中有着重要应用。若序列a1a2…an…满足ai∈{0，1}（i＝1，2，…），且存在正整数m，使得ai＋m＝ai（i＝1，2，…）成立，则称其为0－1周期序列，并称满足ai＋m＝ai（i＝1，2，…）的最小正整数m为这个序列的周期。对于周期为m的0－1 序列a1a2…an…，C（k）＝（k＝1，2，…，m－1）是描述其性质的重要指标，下列周期为5的0－1序列中，满足C（k）≤（k＝1，2，3，4）的序列是（ ）。

A.11010… B.11011…

C.10001… D.11001…

分析：本题是考查数列的新概念问题，考查同学们对新概念的理解及运算能力。本题新定义了序列的周期，可根据新概念，逐一对选项进行验证。

类型二 定义新运算

例2（2021 年全国新高考Ⅱ卷）（多选题）设正整数n＝a0·20＋a1·2＋…＋ak－1·2k－1＋ak·2k，其 中ai∈ {0，1 }，记ω（n）＝a0＋a1＋…＋ak，则（ ）。

A.ω（2n）＝ω（n）

B.ω（2n＋3）＝ω（n）＋1

C.ω（8n＋5）＝ω（4n＋3）

D.ω（2n－1）＝n

分析：本题是考查定义与数列有关的新运算问题，考查同学们对新运算的理解及应用能力。

解：选项A，ω（n）＝a0＋a1＋…＋ak，2n＝a0·21＋a1·22＋…＋ak－1·2k＋ak·2k＋1，所以，ω（2n）＝a0＋a1＋…＋ak＝ω（n），A 正确。

选项B，不妨取n＝2，则2n＋3＝7＝1×20＋1×21＋1×22，所以ω（7）＝3。而2＝0·20＋1·21，则ω（2）＝1。所以ω（7）≠ω（2）＋1，B错误。

选项C，因为8n＋5＝a0·23＋a1·24＋…＋ak·2k＋3＋5＝1·20＋1·22＋a0·23＋a1·24＋…＋ak·2k＋3，所以，ω（8n＋5）＝2＋a0＋a1＋…＋ak。而4n＋3＝a0·22＋a1·23＋…＋ak·2k＋2＋3＝1·20＋1·21＋a0·22＋a1·23＋… ＋ak·2k＋2，所 以，ω（4n＋3）＝2＋a0＋a1＋…＋ak。因此，ω（8n＋5）＝ω（4n＋3），C正确。

选项D，因为2n－1＝20＋21＋…＋2n－1，所以ω（2n－1）＝n，D 正确。

故选ACD。

类型三 定义新情景

例3南宋数学家杨辉在《详解九章算法》和《算法通变本末》中，提出了一些新的垛积公式，其所讨论的高阶等差数列与一般等差数列不同，前后两项之差并不相等，但是逐项差数之差或者高次差成等差数列。对这类高阶等差数列的研究，在杨辉之后一般称为“垛积术”。现有高阶等差数列，其前7 项分别为1，7，15，27，45，71，107，则该数列的第8项为____。

分析：本例是以古典书籍为背景，构造了高阶等差数列的定义，考查同学们对新背景下新定义的理解及应用能力。正确理解高阶等差数列的定义，分别计算前后两项，结合等差数列的定义，可得答案。

解：因为所给数列为高阶等差数列，设该数列的第8 项为x，根据高阶等差数列的定义：用数列的后一项减去前一项得到一个新数列，得到的新数列也用后一项减去前一项再得到一个新数列，即得到了一个等差数列。

如图1：

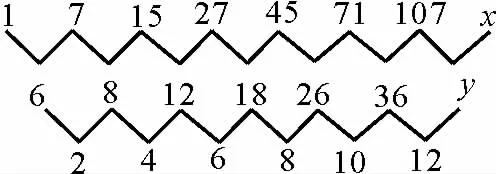
图1

故答案为155。

解答与数列有关的新定义问题的策略：（1）通过给定的与数列有关的新定义，或约定的一种新运算，或给出的由几个新模型来创设的新问题的情景，要求在阅读理解的基础上，依据题设所提供的信息，联系所学的知识和方法，实现信息的迁移，达到灵活解题的目的；（2）遇到新定义问题，需耐心研究题中信息，分析新定义的特点，搞清新定义的本质，按新定义的要求“照章办事”，逐条分析、运算、验证，使问题得以顺利解决。

演练：

1.对于任一实数序列A＝{a1，a2，a3，…}，定义ΔA为序列{a2－a1，a3－a2，a4－a3，…}，它的第n项是an＋1－an。假定序列Δ（ΔA）的所有项都是1，且a18＝a2021＝0，则a2022＝（ ）。

A.1002 B.2004

C.101 D.202

解析：设序列ΔA的首项为d，则序列ΔA为{d，d＋1，d＋2，…}，则它的第n项为d＋（n－1）。

因此，数列A的第n项为：

an＝a1＋（ak＋1－ak）＝a1＋d＋（d＋1）＋…＋（d＋n－2）＝a1＋（n－1）d＋（n－1）·（n－2）。

an是关于n的二次多项式，其中n2的系数是。

因为a18＝a2021＝0，所以an＝（n－18）·（n－2021），a2022＝（2 022－18）·（2022－2021）＝1002。故选A。

2.对于数列 {an}，定义Yn＝为数列{an}的“美值”。现已知某数列{an}的“美值”Yn＝2n＋1，记数列{an－tn}的前n项和为Sn，若Sn≤S10对任意的k∈N*恒成立，则实数t的取值范围是（ ）。

解析：由Yn＝＝2n＋1，可得a1＋2a2＋…＋2n－1an＝n×2n＋1。

当n≥2 时，a1＋2a2＋…＋2n－2an－1＝（n－1）2n；①

a1＋2a2＋…＋2n－1an＝n·2n＋1。②

②－①可 得，2n－1an＝n·2n＋1－（n－1）·2n＝（n＋1）·2n。

所以an＝2n＋2。

当n＝1时，a1＝4也满足上式，故an＝2n＋2，n∈N*。

所以an－tn＝（2－t）n＋2，数列{antn}是等差数列。

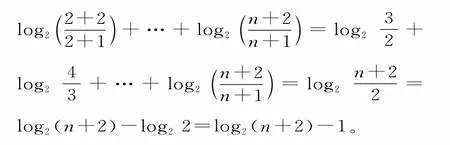
所以，Sk＝log2（k＋2）－1。

因为Sk为正整数，所以log2（k＋2）－1＞0，即k＋2＞2，则k＞0。

令m＝log2（k＋2），则k＝2m－2。

因 为k∈[1，2 021]，所 以2m∈[3，2023]。

因为y＝2x为增函数，且21＝2，22＝4，…，210＝1024，211＝2048，所以m∈[2，10]。

所有“好数”的和为（22－2）＋（23－2）＋…＋（210－2）＝－2×9＝2026。