全国名校必修5综合拔高卷(B卷)答案与提示
一、选择题
1.A 2.C 3.B 4.D 5.D 6.C 7.B 8.C 9.D 10.A 11.A 12.B 13.A 14.C 15.C 16.D 17.D 18.D 19.C 20.B 21.D 22.B 23.D 24.A 25.B 26.D 27.A 28.B 29.C 30.A 31.B 32.B 33.C 34.B 35.B 36.A 37.C 38.C 39.B 40.D
二、填空题

三、解答题
61.(1)an=2n-1。
(2)Sn=n2+n+2n-1。
62.(1)当c=16 时,则f(x)=-x2+a(5-a)x+16。
f(2)=-4+2a(5-a)+16=-2a2+10a+12>0,即a2-5a-6<0。
也即(a-6)(a+1)<0,解得-1<a<6。
该不等式的解集为{a|-1<a<6}。
(2)当a=4时,f(x)=-x2+4x+c。
对任意的x∈(-∞,1],f(x)<0 恒成立,即f(x)=-x2+4x+c<0 对任意的x∈(-∞,1]恒成立,也即c<x2-4x对任意的x∈(-∞,1]恒成立。
所以c<(x2-4x)min,x∈(-∞,1]。
令g(x)=x2-4x=(x-2)2-4,x∈(-∞,1]。
因为g(x)min=g(1)=-3,所以c<-3。
63.(1)由正弦定理及btanA=(2cb)·tanB,得:
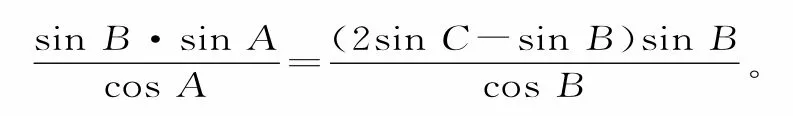
在△ABC中,0<B<π,0<C<π,sinB≠0,sinC≠0,故sinAcosB=(2sinCsinB)cosA=2sinCcosA-sinBcosA。
也 即sinAcosB+cosAsinB=2sinCcosA。故sin(A+B)=2sinCcosA,即sinC=2sinCcosA。又sinC≠0,故cosA=。又0<A<π,则A=。
(2)因 为S△ABC=bcsinA=bc=,所以bc=48。
由余弦定理知,a2=b2+c2-2bccosA,则52=b2+c2-bc=(b+c)2-3bc。
故(b+c)2=3×48+52=196,b+c=14。
64.(1)由题意知,要使不等式mx2-mx-2<0恒成立,则:
①当m=0 时,显然-2<0 成立,所以m=0时,不等式mx2-mx-2<0恒成立;
②当m≠0时,只需,解得-8<m<0。
综上,实数m的取值范围为(-8,0]。
(2)要使对于x∈[1,3],f(x)>-m+2(x-1)恒成立,只需mx2-mx+m>2x恒成立,也即需m(x2-x+1)>2x。

当x∈[1,3]时,ymax=2,故m>2。
65.(1)设等差数列{an}的公差为d。

66.(1)因为∠ADC+∠ABC=π,所以cos∠ADC=-cosθ。
在△ABC和△ADC中分别利用余弦定理得:
AC2=22+62-2×2×6cosθ=42+42-2×4×4(-cosθ)。

在△ABC中由余弦定理知,AC2=22+62-2×2×6cosθ=40-24cosθ。
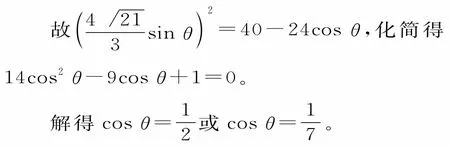
67.(1)因为a,b,c依次成等差数列,且公差为2,所以b-a=c-b=2,b=c-2,a=c-4。

整理得c2-9c+14=0。
解得c=7或c=2(舍去)。
(2)设B=θ,△ABC的外接圆的半径为R,则πR2=π,解得R=1。

68.(1)由题意可得,S1=a1=1,S2=a1+a2=4。
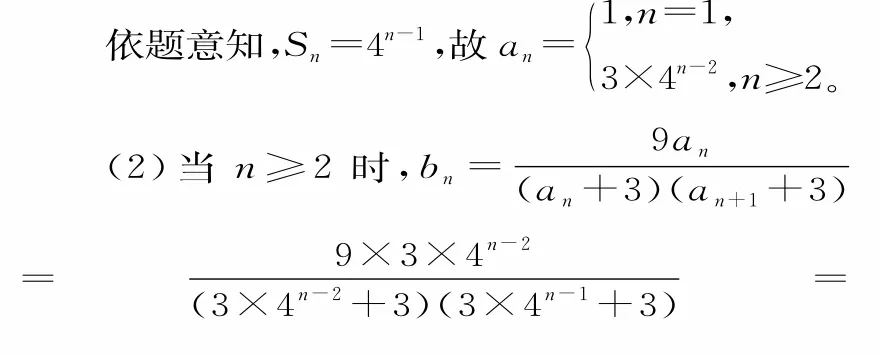

69.(1)因为不等式f(x)≤0 的解集为[1,2],所以:
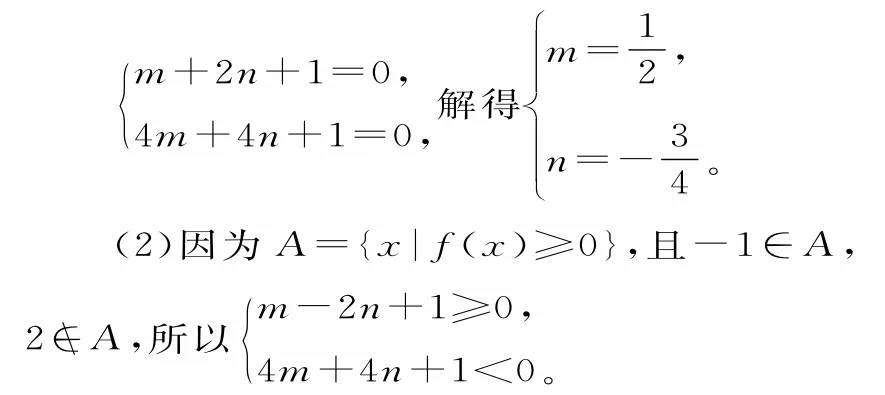
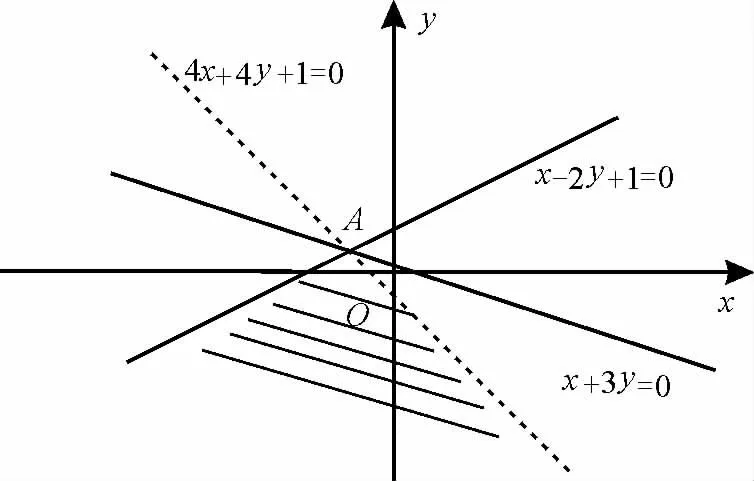
图1