利用对数恒等式解题

安徽省合肥市第四中学(230000) 郑 良 钱兆云

根据对数的定义有: (1)logaab=b(a ＞0 且a /= 1);(2)alogaN=N(a ＞0 且a /= 1,N ＞0). 大家常常把两个公式叫做对数恒等式.[1]以上两个等式从左向右为式子的化简,可视为正用,学生一般不会出现问题;从右到左,由(1)可知任意实数均可写成对数的形式,由(2)可知任意正数均可写成指数的形式.它需要根据所要求解与求证问题的结构调整,可视为逆用,具有一定的灵活性.对于由指数型函数、对数型函数、幂函数型函数等构成的特殊问题,若能合理借助上述对数恒等式(主要指逆用),往往使问题迎刃而解或解题(证明)过程得到优化.

一、真题呈现

1 借助同构构建函数

同构式是指变量不同、结构相同的表达式,多表现为函数对称性的应用.[2]若已知函数f(x)的解析式,正向代入容易得到f(x1),f(x2),反过来,若给出f(x1),f(x2)及变形形式,逆向抽象(构造)出函数f(x)则相对困难,它需要解题者根据结构的相似性进行(不断地)调适,实现相同结构形式的还原与配凑.

例1(自编题)已知函数f(x) =xex(e 为自然对数的底数),g(x) =xlnx,若f(x1) =g(x2) =t,其中t ＞0,则的取值范围是____.

解法1x1ex1=x2lnx2=t,由t ＞0,得x1＞0,x2＞1,所以lnx2＞0,由对数恒等式(2)得x2lnx2=lnx2elnx2=t,由f′(x) = (x+1)ex,函数f(x)在(-1,+∞)上单调递增. 由f(x1) =g(x2) 知f(x1) =f(lnx2), 又x1＞0,lnx2＞0,得x1=lnx2. 所以

设h(t) =则h′(t) =当t ∈(0,e) 时,h′(t)＞0,函数h(t)单调递增,当t ∈(e,+∞)时,h′(t)＜0,函数h(t) 单调递减, 故h(t) ≤h(e) =当t →0 时,h(t)→-∞;当t →+∞时,h(t)→0,所以的取值范围是

解法2由对数恒等式(1) 得f(x) =xex= exlnex,由x1ex1=x2lnx2=t, 由t ＞0, 得x1＞0,x2＞1, 所以x2＞1.g(x) =xlnx,g′(x) = lnx+1, 则函数g(x)在上单调递增. 由ex1lnex1=x2lnx2=t, 即g(ex1) =g(x2),而ex1,x2∈(1,+∞),所以ex1=x2. 所以下同解法1.

点评求解目标中含有相互关联的三个量x1,x2,t, 消元是解题的基本方向, 是局部消元(如直接建构x1与x1分别关于t的函数)还是整体消元(x1x2整体关于t的函数)? 通过对条件的结构分析,配凑相同的结构形式,利用函数f(x)(或g(x))的单调性将x1x2整体用t表示,进而求函数y=的值域. 题设条件一定,所以x1与x2的关系确定(解法1 与解法2 中分别以x1=lnx2,ex1=x2的等价形式呈现),解法1 与解法2 分别以y=f(x),y=g(x)的结构形式为标准进行配凑.

例2(自编题)已知函数f(x) =x+ln(x-1),g(x) =xlnx,若f(x1) = 1+2 lnt,g(x2) =t2,则(x1x2-x2)lnt的最小值为( ).

解由题意f(x1) =x1+ ln(x1-1) = 1 + 2 lnt,即x1-1 + ln(x1-1) = lnt2, 由对数恒等式(1) 得lnt2=ln ex1-1+ln(x1-1)=ln[ex1-1(x1-1)],所以

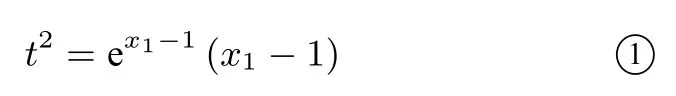
由对数恒等式(2)得

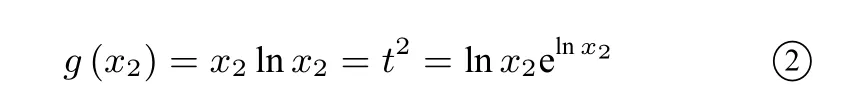
其中t2＞0.

又函数y=xex在[0,+∞)上单调递增,故由①②可得x1-1=lnx2,故(x1x2-x2)lnt=x2lnx2lnt=t2lnt. 记h(t)=t2lnt(t ＞0),则h′(t)=2tlnt+t,令h′(t)＞0,得令h′(t)＜0,得0＜t ＜,故h(t)在上单调递减, 在上单调递增, 故当x=时,即(x1x2-x2)lnt的最小值为所以选C.

点评相比例1,例2 中的变量间关系更加隐性,对学生的变形化归能力要求更高.一旦建构起关于t的函数,问题迎刃而解.

2 求参数范围

含参不等式恒成立、存在性问题是高考的重点与热点问题.如何求含参不等式恒成立问题中的参数范围,一般常有四种方法: (1)函数最值法;(2)分离参数法;(3)图像法;(4)必要性策略法.其中分离参数法只需研究分离后得到的新函数的最值,与新函数的凹凸性无关;图像法往往分离出一次函数(图像为直线),与函数的凹凸性有关; 必要性策略利用特殊与一般的关系,先利用特殊对象确定结论的必要条件.

例3(自编题) 已知函数f(x) =x ·ex - alnx - ax(a ∈R,e 为自然对数的底数). 若对任意x ＞0 恒有不等式f(x)≥1 成立,求实数a的值.

解法1当a ＜0 时,f(x) 单调递增,f(x) 的值域为R, 不满足题意; 当a= 0 时,f(x) =x ·ex(x ＞0),不满足题意.

当a ＞0 时,f′(x)=(x+1)(ex-),其中在(0,+∞) 上单调递增, 可知f′(x) = 0 有唯一解x0, 此时x0ex0=a, 即x0+lnx0= lna. 因此f(x)的最小值为f(x0)=a-alnx0-ax0=a-alna. 记g(a)=a-alna(a ＞0),则g′(a) =-lna,函数g(a)在(0,1)上单调递增,在(1,+∞) 上单调递减, 当a= 1 时,g(a) 取得最大值为g(1)=1,因此g(a)≥1 的解集为{1}. 所以,实数a的取值范围是{1}.

解法2对任意x ＞0 恒有f(x) ≥1, 由对数恒等式(2) 即得elnx+x - a(lnx+x) ≥1, 令x+ lnx=t, 则t ∈R,即et-at-1 ≥0. 记m(t) = et -at-1. 当a≤0时,m(t) 单调递增,m(-1) = e-1+a-1＜0; 当a ＞0时,m′(t)=et-a,所以m(t)在(-∞,lna)上单调递减,在(lna,+∞)上单调递增,所以m(t)≥m(lna)=a-alna-1,只需a-alna-1 ≥0,下同解法1.

解法3et - at -1 ≥ 0 对任意t ∈R 恒成立.当t= 0 时,a ∈R; 当t ＞0 时, 由et -1 ≥at得a≤当t ＜0 时, 由et -1 ≥at得a≥记n(t) =则n′(t) =记φ(t) =et(t-1) + 1, 则φ′(t) =tet, 当t ＞0 时,φ′(t)＞0,φ(t) 在(0,+∞) 上单调递增, 则φ(t)＞0,n(t) 单调递增, 所以= 1(洛 必达法则), 所以a≤1; 当t ＜0 时,φ′(t)＜0,φ(t) 在(0,+∞) 上单调递减, 则φ(t)＞0,n(t) 单调递增, 所以= 1(洛必达法则),所以a≥1. 综上所述,实数a的取值范围是{1}.

点评解法1 以参数a为分类标准,对于参数a的每一个取值均考虑任意x ∈(0,+∞),只需求各类情况下的参数a取值集合的并集. 对于a ＞0,涉及f′(x)的“隐零点”,进而解关于a的不等式; 解法2 利用对数恒等式, 使m(t)与f(x)-1 形式更简洁. 解法3 以自变量t为分类标准,需求三类情况下参数a取值集合的交集. 解法2 与解法3 中,根据et≥at+1 对任意t ∈R 恒成立,从几何背景可直接得到a=1.

例4(自编题)已知函数f(x)=+lnx-x(a ∈R,e 为自然对数的底数),若x ∈[1,+∞)时,不等式f(x)≥-1恒成立,则实数a的取值范围为( ).

解法1f(x) ≥-1, 即a≥对任意x ∈[1,+∞)恒成立.

记g(x) =,x ∈[1,+∞), 则a≥[g(x)]max. 由 于g′(x) =·(lnx - x+ 2), 令h(x) = lnx - x+ 2,x ∈[1,+∞),h′(x) =≤0 ,所以h(x)在[1,+∞)上单调递减,而h(3) = ln 3-1＞0,h(4) = ln 4-2＜0,所以存在唯一的实数x0∈(3,4)使得h(x0)=0,即lnx0-x0+2= 0. 因此,函数g(x)在[1,x0]上单调递增,在(x0,+∞)上单调递减,故当x=x0时,g(x)取得最大值为g(x0)=

由lnx0-x0+2 = 0,得x0-lnx0= 2,又得lnx0=x0-2,则x0= ex0-2. 所以g(x0) =所以实数a的取值范围为

解法2f(x) ≥-1, 即a≥对任意x ∈[1,+∞)恒成立.

记g(x) =,x ∈[1,+∞), 则a≥[g(x)]max. 由对数恒等式(2)得g(x)=令t(x) =x -lnx -1,x ∈[1,+∞),则t′(x) = 1-≥ 0, 所以t(x) ≥t(1) = 0, 因此g(x) =m(t) =其中t≥0,m′(t) =所以函数m(t)在(0,1)上单调递增,在(1,+∞)上单调递减,故当t= 1 时,m(t)取得最大值为所以实数a的取值范围为

解法3f(x) ≥-1, 即a≥对任意x ∈[1,+∞) 恒成立. 记g(x) =x ∈[1,+∞), 则g(x) ≥0. 由对数恒等式(2) 得g(x) =当且仅当x-lnx-2=0 时等号成立.

解法 4f(x) =+ lnx - x,f′(x) =当a≤0 时,f′(x) ≤0,f(x)在[1,+∞)单调递减,而当x ∈(1,+∞)时,有f(x)＜f(1)=ae-1 ≤-1, 矛盾; 当a ＞0 时, 记h(x) =aex -x,x ∈[1,+∞).h′(x)=aex-1,令h′(x)＜0,得x ＜-lna,令h′(x)＞0,得x ＞-lna.

当-lna ＞1, 即a ∈函数h(x) 在[1,-lna]上单调递减, 在(-lna,+∞) 上单调递增, 且h(-lna) =1 + lna ＜0, 而h(1) =ae-1＜0, 当x →+∞时,h(x)→+∞,所以存在x1∈(-lna,+∞)使得h(x1) = 0,即aex1- x1= 0. 因此, 函数f(x) 在[1,x1] 上单调递减, 在(x1,+∞) 上单调递增, 当x=x1时,f(x) 取得最小值f(x1) =+ lnx1- x1. 由aex1- x1= 0, 得=1;又得lna+x1-lnx1=0,即lnx1-x1=lna. 所以f(x1)=1+lna≥-1,得a≥

当-lna≤1, 即+∞), 函数h(x) 在[1,+∞)上单调递增, 而h(1) =ae-1 ≥ 0, 从而f′(x) ≥ 0在[1,+∞) 恒成立, 函数f(x) 在[1,+∞) 上单调递增, 则f(1)=ae-1 ≥-1 满足题意,所以

综上所述,实数a的取值范围为

点评解法1、解法2 与解法3 均为分离参数法,只需求g(x)的最大值. 其中解法1 用“隐零点”实现“设而不求”(实际上也无法求出g′(x)的零点x0的值),根据目标式的结构特征对x0所满足的关系式“lnx0-x0+2=0”变形整理得出g(x0)的值(函数g(x)的最大值);解法2 利用对数恒等式,调整g(x)的结构形式进而整体换元(t(x)=x-lnx-1)使目标函数的形式更简洁. 其最值点x0满足t(x0) = 1,即lnx0-x0+2 = 0. 本质上与解法1 为同一种方法, 通过换元法将目标形式简化, 对应的零点化隐为显. 解法3仍用对数恒等式, 根据最值的定义巧妙变形, 用常见不等式ex≥x+ 1 进行放缩. 解法4 为函数最值法, 其中当时, 需要用h(x) 的“隐零点”牵线搭桥, 通过对“隐零点”所满足的条件式的适当变形实现对f(x1)值的求解. 若用由x ∈[1,+∞)可知更容易确定参数a的分类标准.

例5(自编题) 设f(x) =ax+ lnx+ 1, 若对∀x ＞0,f(x)≤xe2x恒成立,求a的范围.

解法1∀x ＞0,f(x) ≤xe2x,即a≤e2x-对任意x ∈(0,+∞)恒成立. 记g(x)=e2x-,由对数恒等式(2)得g(x) =·(2x+lnx+1-lnx-1)=2,当且仅当2x+lnx=0 时等号成立. 所以实数a的取值范围是(-∞,2].

解法2∀x ＞0,f(x) ≤xe2x, 即a≤e2x -对任意x ∈(0,+∞) 恒成立. 记g(x) = e2x -则g′(x) = 2e2x+记h(x) =2x2e2x+ lnx, 则h(x) 在(0,+∞) 上单调递增,h(1) =存在x0∈使得=0. 因为函数g(x)在(0,x0)上单调递减,在(x0,+∞)上单调递增,所以当x=x0时,g(x)取得最小值g(x0)=e2x0-

由2e2x0+=0,得2x0e2x0=由对数恒等式(2)得,而函数y=tet在(0,+∞)上单调递增,所以2x0=即2x0=-lnx0,所以g(x0) =所以实数a的取值范围是(-∞,2].

解法3∀x ＞0,f(x)≤xe2x,即ax≤xe2x-lnx-1 对任意x ∈(0,+∞)恒成立. 记m(x)=xe2x-lnx-1,x ＞0.m′(x)=(2x+1)e2x-所以函数m(x)为(0,+∞)的下凸函数.m′(x)在(0,+∞)上单调递增, 由＞0, 存在唯一x2∈使得m′(x2) = 0,所以函数m(x)在(0,x2)上单调递减,在(x2,+∞)上单调递增.

设P(x1,x1e2x1-lnx1-1) 为m(x) 图象上的任意一点, 则该点处的切线方程为y -(x1e2x1-lnx1-1) =[(2x1+1)e2x1-](x-x1),代入(0,0)整理得-lnx1=2x21e2x1, 由对数恒等式(2) 得2x1e2x1=而函数y=tet在(0,+∞) 上单调递增, 所以2x1=即2x1e2x1+e2x1-= 2x1e2x1= 2. 所以实数a的取值范围是(-∞,2].

解法4∀x ＞0,f(x) ≤xe2x, 即xe2x -ax-lnx-1 ≥ 0 恒成立. 记n(x) =xe2x - ax -lnx -1, 则n′(x) = (2x+1)e2x - a -则n′(x) 在(0,+∞) 上单调递增, 且当x →0+时,n′(x)→-∞; 当x →+∞时,n′(x)→+∞,所以存在唯一的正数x3使得n′(x3) = 0,即a= (2x3+1)e2x3-因此函数n(x)在(0,x3)上单调递减,在(x3,+∞)上单调递增,当x=x3时,n(x)取得最小值为n(x3)=x3e2x3-ax3-lnx3-1.

由a= (2x3+1)e2x3-得ax3= 2x23e2x3+x3e2x3-1,所以n(x3) =-2x23e2x3-lnx3,由n(x3) ≥0,得2x23e2x3≤-lnx3, 由对数恒等式(2) 得2x3e2x3≤∈(1,+∞), 而y=xex在(0,+∞)上单调递增,所以2x3≤因此a≤=2,当且仅当2x3+lnx3=0 时等号成立.

点评解法1 与解法2 均为分离参数法, 解法1 聚焦函数最值的定义, 对照g(x) 的分母x利用常用不等式ex≥x+1 放缩求解. 解法2 直接对函数g(x)求导, 然后对函数g′(x)的“隐零点”所满足的条件式变形化简得到函数g(x)的最小值. 若没有解法1 的铺垫, 多数学生难以将“2e2x0+= 0”简化为“2x0=-lnx0”,导致解法2 的无疾而终. 解法3 为图像法,利用函数m(x)为先减后增的下凸函数,根据其几何意义先求参数a的临界值. 解法4 为函数最值法,即用n(x3) ≥0,通过n′(x3)的“隐零点”不易将n(x3)用a表示进而求解关于a的不等式,此处以退为进先建立关于x3的不等关系,再利用a与x3的函数关系确定参数a的取值范围. 由于x0,x1分别对应于参数a的边界值2,故x0=x1.

3 证明不等式

含参不等式求参数的取值范围本质是找使不等式成立的参数a的取值集合,即找到使不等式成立的充要条件,而含参不等式证明中给出的参数的取值范围只是使不等式成立的参数a的取值集合的子集,即使不等式成立的充分条件.因此可选择直接证明,也可以求出使不等式成立的参数的取值范围,再判定它与条件中给出的参数的取值范围之间的子集关系.

例6(合肥市2021年高三第二次教学质量检测数学试题(理科)第21 题)已知函数f(x)=a(x+2)ex-(x+3)2(a ∈R,e 为自然对数的底数).

(1)讨论函数f(x)的单调性;

(2)当a ＞时,证明:f(x-2)＞lnx-x2-x-3.

解(1)从略. 以下考虑(2)的证明.

证法1当a ＞时,要证f(x-2)＞lnx-x2-x-3,即要证axex-2＞lnx+x -2, 也即证a ＞(x ＞0). 记g(x) =(x ＞0), 则g′(x) =记φ(x) = 3-lnx-x,则φ(x)在(0,+∞)上单调递减,φ(1) = 2＞0,φ(3) =-ln 3＜0,所以存在x0∈(1,3),使得

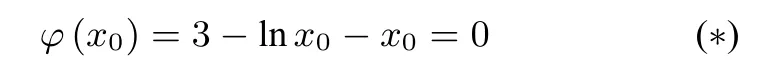
当x ∈(0,x0) 时,g′(x)＞0; 当x ∈(x0,+∞) 时,g′(x)＜0. 所以g(x) ≤g(x0) =由(*) 知lnx0= 3- x0, 得e3-x0=x0, 所以g(x0) =所以g(x) ≤＜a. 所以当时,f(x-2)＞lnx-x2-x-3.

证法2当a ＞时,要证f(x-2)＞lnx-x2-x-3,即要证a ＞(x ＞0), 由对数恒等式(2) 得g(x) =记t(x)=lnx+x-2,则t(x)是(0,+∞)上的增函数,t(x)∈R,则g(x) =m(t) =则m′(t) =所以函数m(t)在(-∞,1) 上单调递增, 在(1,+∞) 上单调递减, 所以当t= 1 时,m(t) 取得最大值为所以当a ＞时,f(x-2)＞lnx-x2-x-3.

证法3同解法2,由对数恒等式(2)得

当且仅当lnx+x-3=0 时等号成立.

证法4当a ＞时,要证f(x-2)＞lnx-x2-x-3,即要证axex-2＞lnx+x-2. 记h(x)=axex-2-lnx-x+2,x ＞0),h′(x)=(x+1)(aex-2-

记n(x) =aex-2-,x ＞0), 则n(x) 在(0,+∞) 上单调递增, 当x →0+时,n(x)→ -∞; 当x →+∞时,n(x)→+∞. 存在x1∈(0,+∞) 使得n(x1) = 0, 即aex1-2-= 0. 所以h(x) 在(0,x1) 上单调递减,在(x1,+∞)上单调递增,所以h(x) ≥h(x1) =ax1ex1-2-lnx1-x1+2=-lnx1-x1+3.

由aex1-2-=0,得ax1ex1-2=1,即lna+lnx1+x1-2 = 0,得lnx1+x1= 2-lna,所以h(x) ≥h(x1) =1+lna ＞0.

证法5当a ＞时,要证f(x-2)＞lnx-x2-x-3,即要证axex-2＞lnx+x-2,只需证xex-3≥lnx+x-2对任意x ∈(0,+∞)恒成立,即证xex-3-lnx-x+2 ≥0.证明过程与证法4 类似(或直接利用ex≥x+1 放缩).

点评证法1(命题组给出的参考答案) 为分离参数法,根据函数g′(x) 的“隐零点”实施过渡; 证法2 应用对数恒等式并换元使m(t)比g(x)的形式更简洁; 证法3 应用对数恒等式后用常见不等式ex≥x+1 放缩; 证法4 直接对求证目标移项作差求函数h(x) 的最小值, 也需用到函数h′(x)的“隐零点”实施过渡; 证法5 根据a ＞利用边界值对函数进行放缩,再利用不等式的传递性;事实上,原问题等价于ax-,x ＞0)恒成立,若记p(x)=ax-,x ＞0),则函数p′′(x)不含参数,其“隐零点”范围能够确定,而p′(x)的“隐零点”与参数a有关,其相对精确的范围不易确定. 证法2(或证法1)通过对m(t) (g(x))的研究了解函数m(t) (g(x))的全貌,而证法3 只是验证了m(t) (g(x))最大值的取得.

二、几点思考

1 夯实基础知识,构建知识网络

数学的学习一定要夯实基础, 把最基础的内容作为知识、思想方法的生长点. 基础知识、基本思想方法、基本活动经验本身就是数学模型, 只有深刻理解才能将其内化为能力与素养. 如对数的基本功能是化复杂为简单, 如logaMN=logaM+logaN=logaM -logaN)化乘(除)为和(差),logaMn=nlogaM化乘方为倍数. 恒等变形是基本功,命题时往往从基础开始不断变形,最终将试题以与基本出发点面目全非的形式呈现,需要学生具备一定的观察与抽象能力将其还原并识别出来. 如例1 与例2 中的y=xex,例4 解法3 与例5 解法1 中的ex≥x+1,例4 解法2 与例6 解法2 中m(t) =根据最值的概念明确变形的方向容易得到例5 的解法1.

2 多方对比切入,深化问题理解

解题不能满足于看懂答案, 应着眼于数学思想的领悟, 方法的创新, 理解的突破. 解题过程中, 若能不断地比对特殊与一般, 局部与整体, 则会更有利于理解与揭示问题本质. 如应用对数恒等式转化的条件(正数才能写成指数的形式) 及能带来方便的原因(整体换元) 等.如例3 中可得et -1 ≥at对任意t ∈R 恒成立, 若用et -1 ≥t≥at对任意t ∈R 恒成立, 得到a= 1 则不符合逻辑. 又如含参不等式的参数范围与含参不等式(给出参数范围) 的证明之间的逻辑关系. 如例3 可改为“当a= 1 时, 证明: 对任意x ＞0,xex -alnx-ax≥1”(即xex -ln-x≥1),例4 可改为“当a≥时,证明: 对任意x≥1,xex-alnx-ax≥1”,也可调整为“当a≥时,证明: 对任意x≥1,xex-alnx-ax≥1”.

3 理解学生现实,谋划稳步推进

“题海战术”高耗低效,教与学中尽可能以学定教,做到精准. 解题前要预计各种方法的可行性? 可行方法的优劣?解题中要根据思维受阻的情况及时调整. 解题后要加强反思,如方法为什么不行或可行? 方法优或劣在哪里? 有没有更为顺畅的思维与解题策略等,力争“做几题,通一类”. 教师要根据学情,教学时适时铺垫,分步实施. 如在以上解答中,还可尝试让学生将隐零点所在的范围用有穷区间来表示等.