圆幂定理与著名几何问题的联系及解题妙用

杭州第十四中学(310006) 朱成万

在平面几何中, 相交弦定理、切割线定理及割线定理统称为圆幂定理. 该定理表示过一定点作两条直线与圆相交,则定点到每条直线与圆的交点的两条线段的积相等,且积为定值. 即设圆O半径为r, 过一定点P作两条直线分别与圆O相交于A,B和C,D, 则PA·PB=PC ·PD这个定值为叫做点P关于⊙O的幂.

当点P在圆内时,为相交弦定理(图1);当点P在圆外时为切割线定理,即点C,D重合时,为切线定理(图2),否则为割线定理(图3).

图1

图2

图3

圆幂定理与许多数学问题有紧密联系, 比如极化恒等式、米勒问题、四点共圆问题等,研究它们的联系,能加深对问题的理解,揭示问题的本质所在.

一、极化恒等式与圆幂定理

设a,b是两个平面向量,则:

我们称式(1)为极化恒等式. 如图4 所示,式(1)也可表述为:

图4

我们可以用极化恒等式来证明圆幂定理, 如图5 所示,设PB是圆O的切线,B为切点,则

图5

显然,式子(2)(3)不论是代数表述,还是几何含义都是一致的. 不仅揭示了三角形的中线与边长的关系,更揭示了圆幂定理和极化恒等式的内在联系.

下面试举两例,体会它们在解题中的妙用.

例1(2020年江苏重点中学联考试题改编) 设椭圆+y2= 1,F是椭圆C的右焦点, 点M是直线l:x= 2 上的动点,过点F作OM的垂线与以OM为直径的圆交于点N,求线段ON的长.

解法一(圆幂定理) 如图6, 因为OM⊥NF于Q,OP⊥l于P, 所以P,F,Q,M四点共圆, 由圆幂定理有OQ · OM=OF · OP= 1×2 = 2, 由题知ON2=|OQ||OM|= 2, 所以

图6

解法二(极化恒等式)设F(1,0),M(2,m),则MF的中点由题知

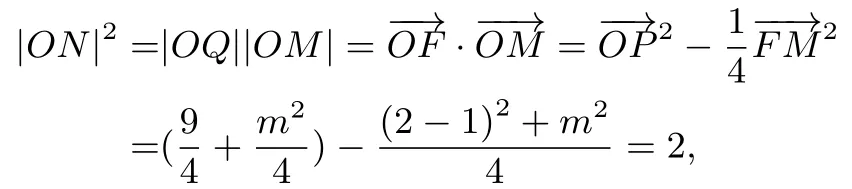
本题的两种解法,用圆幂定理与用极化恒等式本质上是一致的. 相比较而言,用圆幂定理求解更简洁.

例2(2017年高考浙江卷第21 题)如图7,已知抛物线x2=y.点抛物线上的点P(x,y),过点B作直线AP的垂线,垂足为Q.

图7

(1)求直线AP斜率的取值范围;

(2)求|PA||PQ|的最大值.

解(1)略.

(2) 因为QB⊥AQ,所以Q在以AB为直径的圆上,则AB中点为根据圆幂定理有

令t(x)=-x4+则t′(x)=-4x3+3x+1 =-(x-1)(2x+1)2,显然当x= 1 时,|PA|·|PQ|最大,最大值为

本题关键是得到式子(4), 用圆幂定理几乎可以做到秒杀, 比之其他的方法, 比如分别用两点间距离求|PA|和|PQ|,运用圆幂的优势是显而易见的.

二、米勒问题与圆幂定理

几何学史上著名的米勒问题即张角最大问题:“设点M,N是锐角∠AOB的一边OA上的两点,试在OB边上找一点P,使得∠MPN最大. ”其结论是“点P为过M,N两点且和射线OB相切的圆的切点”,如图8 所示. 由圆幂定理|OP|2=|OM||ON|,则可度量点P的位置.

图8

例3(2005年高考浙江卷理科第17 题) 如图9, 已知椭圆的中心在坐标原点, 焦点F1,F2在x轴上, 长轴A1A2的长为4, 直线l:x=与x轴的交点为M,|MA1|:|A1F1|=2:1.

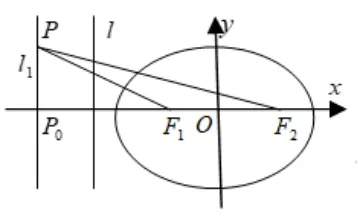
图9

(1)求椭圆的方程;

(2)若直线l1:x=m(|m| ＞1),P为l1上的动点,使∠F1PF2最大的点P记为Q,求点Q的坐标(用m表示).

解(1)解略(答案为=1).

(2) 如图10, 过F1,F2作圆与直线l相切, 设切点为Q,则∠F1QF2是∠F1PF2的最大值. (因为对于l1上其他点P′,则有∠F1QF2= ∠F1EF2＞∠F1P′F2, 这 也 就 证 明 了 米 勒问题.) 设P(m,y0),|m| ＞1, 由圆幂定理有|y0|2=NF1· NF2= (m -1)(m+1), 即=|y0|, 所以

图10

例4(2006年高考全国卷理科第16 题) 已知椭圆= 1 的左右焦点分别为F1,F2, 点P在直线l:x-= 0 上. 当∠F1PF2取最大值时,求的值.

解由米勒问题知, 要使∠F1PF2最大, 则过F1,F2,P三点的圆必定和直线l相切于P点. 设直线l交x轴于A(-8-0), 则∠APF1= ∠AF2P, 即ΔAPF1∽ΔAF2P,即

又由圆幂定理有

而从而有由①②得

例5(2005年高考天津卷理科第20 题) 某人在一山坡P处观看对面山项上的一座铁塔, 如图11 所示, 塔高BC= 80(米),塔所在的山高OB= 220(米),OA= 200(米),图中所示的山坡可视为直线l且点P在直线l上,l与水平地面的夹角为α,tanα=试问此人距水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高).

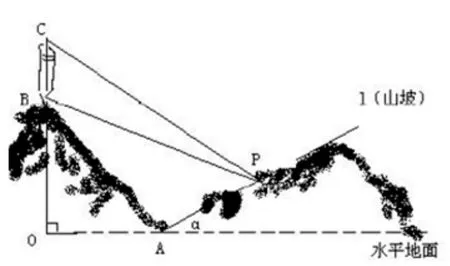
图11

解如图12,过点B,C作圆M与直线l相切,则切点P的纵坐标即为所求. 设直线l与y轴交于点Q,易得Q(0,-100). 由圆幂定理得|QP|2=|QB|·|QC|=320×400, 则|QP|=由 于tanα=所 以sinα=所以yP+ 100 =|QP|sinα=所以yP=60.

图12

学生学过了解析几何,一见到坐标系就习惯性地选解析法去做. 殊不知解析几何的根在平面几何,而平面几何的一些定理正是减少解析几何计算量的强大武器. 比如本题采用圆幂定理与米勒问题,使得该问题的计算量大大减少.

三、圆幂定理与四点共圆

如果平面上存在点A,B,P,Q,M,使得式子|AM||MB|=|PM||MQ|成立,则A,B,P,Q四点在同一圆上. 这是圆幂定理的逆运用,即用它来解决四点共圆问题.

例6(2011年高考全国卷理科第21 题)已知O为坐标原点,F为椭圆C:x2+=1 在y轴正半轴上的焦点,过F且斜率为的直线l与C交与A,B两点,点P满足

(1)证明: 点P在C上;

(2)设点P关于点O的对称点为Q,证明:A,P,B,Q四点在同一圆上.

解(1)设l:y=+1,将其椭圆C方程联立得到:解得

(2)因为P,Q关于点O对称,所以由题意知线段AB与PQ相交于AB的中点M,则可得|AM|=|BM|= 所以|AM||MB|=|PM||MQ|.

由圆幂定理可知,A,B,P,Q四点在同一圆上.

例7(2014年高考全国卷理科第21 题) 已知抛物线C:y2=2px(p ＞0)的焦点为F,直线y= 4 与y轴的交点为P,与C的交点为Q,且|QF|=

(1)求C的方程;

(2)过F的直线l与C相交于A,B两点,若AB的垂直平分线l′与C相较于M,N两点,且A,M,B,N四点在同一圆上,求l的方程.

解(1)解略(答案为y=4x2);

(2)设直线l与l′交于点Q(x0,y0), 故可设l的方程为y-y0=k(x-x0),代入y=4x2得-y+y0-kx0=0.

设A(x1,y1),B(x2,y2),则

四、圆幂定理与代数结构|PT|2 =λ|PA|·|PB|

显然,代数式结构“|PT|2=λ|PA|·|PB|”可以看作是圆幂定理的推广,特别地,当λ= 1 时,则是切割线定理. 所以遇到这种代数结构,可以考虑用圆幂定理求解.

例8(2016年高考浙江卷理科第16 题(1))在ΔABC中, 内角A,B,C所对的边分别为a,b,c. 已知b+c=2acosB. (1)证明:A=2B.

分析b+c=2acosB=,即a2-b2=bc,即a2=b(b+c). 又a2=b(b+c)恰似圆幂定理的形式,故可用圆幂定理证明.

证明如图13, 过B作BC的垂线,和AB的中垂线交于点O, 以O为圆心,OB为半径作圆,则CB与圆O相切于点B,且圆O过点A. 延长CA交圆于另一点F.

图13

根据圆幂定理有BC2=AC ·CF,即a2=b(b+AF),又有a2=b(b+c), 所以AF=c. 因此AB=AF, 所以∠ABF= ∠AFB. 而由平面几何知识知∠AFB= ∠ABC,所以∠ABF= ∠AFB= ∠ABC. 而∠CAB= ∠ABF+∠AFB=2∠ABC,所以A=2B. 命题得证.

例9(2016年高考四川卷理科第20 题) 已知椭圆E:= 1(a ＞b ＞0) 的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线l:y=-x+3 与椭圆E有且只有一个公共点T.

(1)求椭圆E的方程及点T的坐标;

(2)设O是坐标原点,直线l′平行于OT,与椭圆E交于不同的两点A,B,且与直线l交于点P. 证明: 存在常数λ,使得|PT|2=λ|PA|·|PB|,并求λ的值.

解(1)椭圆E的方程为=1. 点T(2,1).

则椭圆变为圆x′2+y′2=6,如图14,图15 所示,由圆幂定理有|P′T′|2=|P′A||P′B|.则所以所以所以因此存在λ且λ=

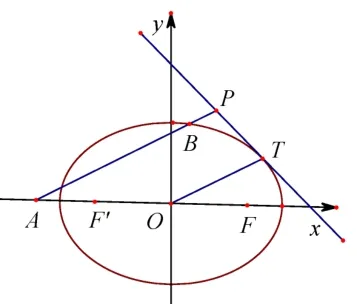
图14

图15

上述几个例题都是用圆幂定理解决问题,比起纯粹代数运算,圆幂定理充分揭示了问题背后的几何问题,将表面纷繁芜杂的问题,化为简约明了的几何直观. 本文旨在以四类问题为载体,培养直观想象的核心素养,发挥数学的内在的价值,以数学的方式育人.