例谈双元不等式证明的转化策略

浙江省临海市灵江中学 (317000) 李秀英

在一些高考压轴题中，常出现证明关于两个变元x1,x2的不等式，这是一类比较复杂的问题，需要有很强的思考能力和高超的数学素养，当然也需要丰富的解题技巧.常用的解题方法是：一是转化，即由已知条件入手，寻找两个变元所满足的关系式，并把含两个变元的不等式转化为含单元的不等式；二是巧构造函数，再借用导数，判断函数的单调性，从而求其最值；三是再回归到两个变元的不等式的证明，把所求的最值应用到两个变元不等式，即可证得结果.本文从几个典型例题的分析求解出发，以评注揭示证题中变形转化的核心所在，希望能够同学们的复习迎考有所帮助.

1、合理配凑

评注：由于题目是要证明关于x1+x2的不等式，在对条件式变形过程中必须注意这个关系式，通过合理配凑，将问题转化为求x1+x2关系式的值域，明确了下一步解题的方向.

2、抓住特点

评注：由于x与2a-x关于x=a对称，所以f(x)与f(2a-x)在同一个单调区间内，抓住这个特殊条件将两个函数式配凑在一起是一个很好的选择.

3、主动拼接

评注：根据零点条件只能得到两个孤立的等式，很难建立两个变元x1、x2之间的关系，通过反向分析，采取对二式分别相减和相加，主动建立起两变元的联系，然后再消元处理，这就寻找到了一个满足条件的函数式.

4、消参列式

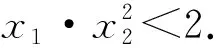
评注：通过不等式的等价变形，将两个根分布在不等式两侧，然后再利用函数的单调性转化为对应函数值之间的大小关系.通过消掉与题目结论无关的参数b，建立了变元x1、x2都符合的函数关系式，下面只要确定函数式的符号就行了.

5、替换求解

评注：由于直接将两个变元x1、x2凑到一起非常困难，本解法就采用了迂回战术，通过对有极值的条件进行合理运用，引入新参数α,β，然后再寻找变元x1、x2与它们之间的关系，使要证的关系式变为与α,β相关的式子，通过求导法就容易解题了.