与其说教解法，不如说教想法——理想的解题教学之我见

江苏省沙溪高级中学 (215421) 谭海洋

解题教学，是数学教学重要的组成部分.解题教学的目的是什么，最直白的说法就是让学生学会如何解题.于是习题课上，教师们往往十分注重解题方法的传授，都希望借助一个问题的解决来突破一类问题的解法，期待通过“一例多练”来达到理想的教学效果，然而往往事与愿违，虽然有些相类似的题目在课堂上教师讲了多遍，学生也练了多遍，但考试中学生对这些题目依然“视若路人”.那么原因何在？难道教师重视解法的教学有错？的确，实践证明只注重传授解法的解题教学是达不到理想的教学效果的.笔者倒认为，对于解题教学，与其说教解法，不如说教想法，教学生“想法”才是理想的解题教学.本文结合教学案例谈谈自己的看法.

1、引导学生仔细审题，独立思考，说出“想法”

审题，是解题的“前奏”，学生解题失败往往是因为他们缺乏对题目的认识，缺乏独立思考的能力，为此教师在解题教学中应引导学生加强审题训练，有意识的设置思维障碍，有时可以让学生在“形同质疑”题中“吃点亏”，从内心深处感悟审题的重要性，并通过对比与思考，说出自己的“想法”.

案例1 一道函数综合题的解法纠错

高一阶段学习了函数内容后，笔者上了一堂函数综合应用的习题课，给出了如下题让学生独立解答.

例1 已知函数f(x)=loga(ax2-x+2)值域为实数集R，求实数a的取值范围.

在解题前，我要求学生认真审题，再交流自己的“想法”.

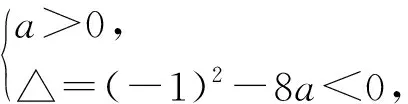
对于这种解法，几乎三分之二的学生认为正确，而其余学生则不认同，但说不出所以然来，于是笔者给出例1的变式题：

变式已知函数f(x)=loga(ax2-x+2)定义域为实数集R，求实数a的取值范围.

定义域为实数集R就是ax2-x+2>0恒成立，不就是学生1的解答吗？一字之差，怎么会答案完全一致呢？笔者要求学生再次审题，独立思考，并说出自己的“想法”.

学生2：学生1的解答是错误的，他把定义域为R当成了值域为R.我认为值域为R，并不要求定义域为R，而“定义域为R”也不能保证“值域为R”，其实只需内函数y=ax2-x+2的值域中含有(0,+∞)即可.我是这样解的：

当a=0时，函数y=ax2-x+2即为y=-x+2，一次函数的值域为R，含有(0,+∞)，符合；

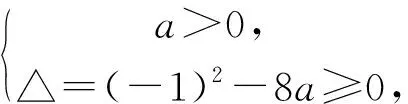
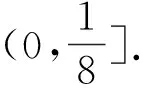
至此，例1的正确解法已“浮出水面”.在教师的引领下，学生不仅注意到审题的重要性，同时也发表了自己的“想法”，在互相补充与完善中，不断提升数学思维能力.

从本案例可以看出，引导学生独立思考，说出“想法”，是解题教学的必由之路，从本质上看，这个教学环节是教师引导学生如何分析问题.试想，如果教师一味地讲解法，却忽视问题的分析，那么学生怎么可能实现“解决问题”的最终目的！

2、引导学生质疑补充，独立动手，实施“想法”

在许多教师看来，解题教学就是教会学生形成解题思路，学生在教师引导下产生解题的“想法”便认为是“大功告成”了，于是教师会迫不及待的换上一个新的问题继续探讨.表面上看似乎加大了教学容量，学生会收益更多，其实不然，这种解题教学模式，会造成学生“只会说，不会做”，这种“眼高手低”现象归咎于只有理论指导没有实战演练.常言道：纸上得来终觉浅，实践才可出真知.笔者以为，解题教学，学生实战演习的环节不可少，教师应该引导学生质疑补充，独立动手，实施学生各自的“想法”.

案例2 一道解析几何题的解法质疑

解析几何的重要教学目标是培养学生数学运算的核心素养，在教学中我们发现，对于解析几何题的解法，学生们大都说个子丑寅卯，但考试时失分却很严重，其根本原因主要有选择方法不当或计算不过关，为了解决这个问题，笔者在圆锥曲线习题课上，给出如下问题要求学生确定解题策略，并加以独立解答.

学生1：本题是直线与圆锥曲线位置关系含参问题，一般可借助“设而不求”的技巧，利用一元二次方程根的判别式与根与系数的关系来求解，我的解法如下：

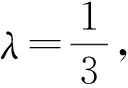
学生3：学生2的解法虽然优于学生1的解法，但我感觉还是计算量太大，而且需分类讨论，一旦忘记了直线AB斜率不存在的情形，最终会导致解答对而不全的严重后果.而我利用了向量共线所得到两个关系式(横坐标与纵坐标的关系都利用)来解，感觉比他们简捷.

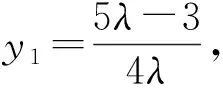
师:第三位同学的解法虽然没有对x1+x2与x1x2的整体代入变形，但是计算量明显比前两位同学的解法小，而且由于没有新的参数k，使得字母较少，变形的目标更加明确.因此我们解答直线与圆锥曲线的问题时，不要过分依赖一元二次方程根的判别式与根与系数的关系，当解方程组比较简单时，不妨直接求出有关未知数的解，然后利用未知数的取值范围建立不等式.

从本案例可以看出，学生说出“想法”诚可贵，但实施“想法”价更高.实施“想法”的过程中，能让他们的数学思维暴露得更真实，能让他们在互相质疑中，不断提高认识，完善解答，提升数学素养，这不正是解题教学的目的吗？由于实施“想法”要有充分的时间，所以教师应该舍得把解题的时间还给学生，宁可少讲一道题，也要让他们把“想法”变成“现实”.

3、引导学生提炼思想，一题多变(多解)，升华“想法”

在解题教学中，教师不仅要教学生如何解题，更要教学生研究题目，研究题目的背景与知识点，研究解题的解法或解法中蕴含的数学思想，研究题目的可变性等要素，只有这样，才能提升他们的数学思维水平，升华他们的“想法”，才能让解题教学达到“通过一道题，解决一类题”的理想境界.

案例3 一堂基本不等式应用的探究课

基本不等式堪称求解最值问题的利器，面对一个具体问题，教师不仅要让学生产生创造条件善于应用基本不等式的“想法”，更要让他们站在命题者的角度去尝试“变(编)题”，举一反三，从而从而实现把知识转化为能力的目的.基于此，笔者上了一堂基本不等式应用的自主变式探究课.

教师给出例题，要求先学生解答例题，并在例题基础上围绕基本不等式的应用进行趣味横生的“变式接龙”活动.

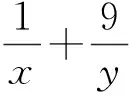
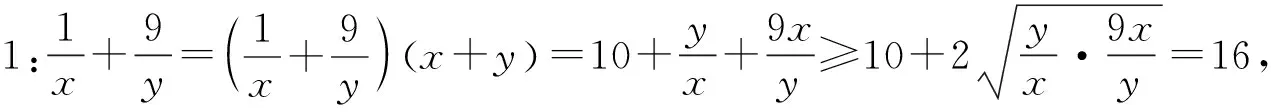
师：此类问题的特点在于已知条件中变量位于分子(或分母)位置上，所求表达式变量的位置恰好相反，位于分母(或分子)上，则可利用常数“1”将已知与所求进行相乘，从而得到常数项与互为倒数的两项，然后利用基本不等式求解.下面请同学们根据例题围绕基本不等式的应用自主变式，并交流发言.

学生2：我由x+y=1联想到sin2α+cos2α=1，于是把它变成一个三角函数最值问题：

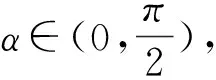
学生3：我把条件与结论互换，得到如下变式：

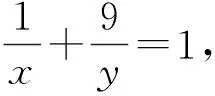
学生4：我把条件变成直线方程的背景，得到如下变式：

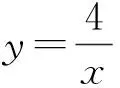
学生5：我把例题的条件与所要求的最值的代数式都变得复杂些：

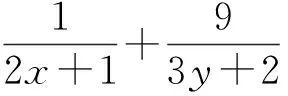
学生6：我把例题的条件与所要求的最值的代数式都变得复杂更复杂：

学生7：刚才大家编的题目都是变量一次型的，我编了个二次型的：

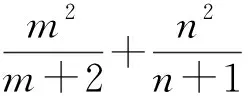
学生8：我把条件等式和所求最值的代数式都变成二次型：

……

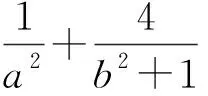
真是一石激起千层浪，学生们跃跃欲试，几乎每位学生都展示了自己的“佳作”.实际上，提出问题比解决问题更重要.解题教学，教师不仅要引导学生解决问题，更要引导学生提出问题，因为这是一条提炼思想，升华“想法”的“绿色通道”.从本案例可以看出，一个问题的解决不是解题教学的结束，而是点燃学生“想法”的“导火索”.在解题教学中，教师应该充分相信学生，把思考的时间与空间还给学生，并积极加以引导，那么，学生的数学思维与能力必将得到升华，这样的课堂必然会活力四射.

什么是理想的解题教学？笔者以为，让学生对数学题有“想法”，实施“想法”，并循着数学规律不断产生新的“想法”的解题教学才是理想的解题教学，因为这种教法不仅符合学生的认知规律，而且能让学生的核心素养得到全面发展.