基于爆源子结构的爆炸问题多尺度分析方法

李述涛，宝 鑫，刘晶波，陈叶青

(1.清华大学 土木工程系，北京 100084；2.军事科学院 国防工程研究院，北京 100036)

爆炸荷载具有强冲击、短持时、大变形等特点，显式有限元方法是目前进行不同介质中炸药爆炸及爆轰波传播数值模拟的主要研究方法。在此类分析中，有限元模型的网格尺寸对计算结果的影响较为显著[1-5]，通常需要设置细密的网格以捕捉爆炸荷载中的高频成分。显式时域逐步积分算法中，满足稳定性条件的最小时间步长与模型中的最小单元尺寸密切相关[6-8]，网格尺寸与计算效率的平衡长久以来是爆炸问题数值模拟研究中的重要挑战之一。

在近爆源问题中，若炸药距离目标较近，一般考虑建立炸药-介质-目标的整体计算模型，在可以接受的计算成本范围内，尽可能地提高单元密度，以获得较为准确的计算结果。而当爆源距离目标较远时，例如水下爆炸对大坝的影响、岩土中爆炸对深埋隧道的作用等问题，即便通过人工边界技术截取有限的计算区域，整体模型的空间尺度仍然较大。尽管随着地冲击波传播距离增加，峰值持时会逐渐增大，高频成分逐渐衰减，目标及其周边介质的网格尺寸也可以适当增大[9-10]。但由此带来的单元尺寸过渡问题将给建模带来一定困难，特别是三维模型，同时，炸药与周边介质的局部高密度网格仍将严重制约整体模型的计算效率。此时采用整体模型进行计算分析恐难以施行。

解决上述问题的思路之一是将爆源与目标分离，根据有限元理论构建一种能够转化爆炸荷载的方法，通过荷载和网格尺度的转换，间接完成整体模型的计算。近期的一些地震动输入问题的研究成果给予上述思路以支持和启发：Liu等[11]根据波场分解理论，提出了基于内部子结构的地震波动输入方法(internal substructure method,ISM)和基于人工边界结构的地震波动输入方法(boundary substructure method,BSM)[12-13]。两种方法均是利用子结构将外源地震波动转化为内源形式下的等效地震荷载，将地震动输入至子结构所包围的内部区域。Bao等[14]针对深埋地下结构的情况，对内部子结构地震波动输入方法进行了改进，使用封闭式的内部子结构实现地震波场由外至内的输入，并针对典型的土-结构相互作用问题进行了计算，验证了内部子结构方法的实用性[15]。

与地震反应分析不同的是，爆炸过程的数值模拟本身属于内源波动问题，爆炸波由模型内部产生，并向外界传播。针对此类问题，可以借鉴内部子结构地震波动输入方法的思想，将近爆源波场转化为爆炸等效荷载，并构建适宜的网格尺度过渡的方法，实现大范围空间的爆炸波传播模拟。Li等[16]提出一种场地地震反应多尺度分析方法，利用人工边界子结构将粗网格的自由波场运动转化为作用在细密网格模型中的等效地震荷载，实现了大范围工程场地的地震反应计算。

基于以上思路，本文发展了一种基于爆源子结构的爆炸问题多尺度分析方法，该方法将爆炸问题中的整体模型拆分为近爆源小尺度模型和大尺度模型，利用黏弹性人工边界[17-18]良好的吸波性能，将近爆源小尺度模型中的自由波场运动转化为大尺度模型中的等效爆炸荷载，从而完成针对大范围爆炸问题的多尺度计算分析。通过与整体模型直接计算的结果对比，验证了本文方法的计算精度。本文方法克服了整体模型难以解决的网格过度与计算效率问题，在满足计算精度的前提下，大幅提高了计算效率，具有较高的实用性。

1 爆源子结构理论

以典型深埋地下隧道结构为例，建立爆炸荷载作用下的二维爆源-介质-目标模型，如图1所示。在截断边界处设置人工边界单元以吸收外行散射波[19]。为保证计算精度，人工边界一般设置在距离结构较远的位置。

图1 爆源-介质-目标模型示意图Fig.1 Source-medium-target model

炸药起爆后，一部分能量导致土体发生相变(固态到液态的变化)和产生塑性变形，一部分耗散于“成坑效应”，除此之外，大部分爆炸能量瞬时转化为在介质中传播的应力波，迅速向四周扩散，形成地冲击效应[20-21]。部分应力波经过复杂介质，传播到达地下结构处，造成结构损伤破坏，而到达截断边界处的地冲击应力波和经地下结构散射及经自由地表反射的波动将被人工边界有效吸收。图1中近爆源区域包含爆炸空腔、塑性破碎区和弹塑性区等，集中了炸药瞬时爆炸产生的大量爆轰产物和迅速向四周膨胀的高频冲击波，其化学反应和动力响应的过程极为复杂[22]。针对该区域的有限元数值模拟需利用流固耦合算法，划分细密网格，充分考虑介质大变形和材料失效等非线性问题[24-26]。

由于介质阻尼的存在，当地冲击应力波远离爆源区域时，应力波的持时逐渐增大，其中的高频成分逐渐衰减，在有限元计算时，远离爆源区域的单元尺寸可以适当增大。此外，研究人员所关心的爆炸波与深埋地下结构的动力相互作用一般也发生在这一区域。鉴于此，可基于波场分解理论，将整体模型分离为含有爆源的小尺度内源模型和不含爆源的介质-目标相互作用大尺度模型，并在两者的交界区域将爆炸波转化为爆炸荷载，从而实现爆炸过程的多尺度分析。

根据地震波动输入法理论[27]，入射地震波在转化为等效输入荷载时，仅与自由波场有关。同样，以爆源为中心向四周扩散的地应力波在进行波动-荷载转化时只与自由场有关，而与地下结构无关。鉴于此，可首先建立与实际爆源-介质-结构模型对应的爆源-自由场模型，该模型为图1中黄色区域(近爆源区域)，在近爆源区域四周设置二维黏弹性人工边界单元，如图2所示。需要注意的是，为保证等效爆炸荷载空间位置的对应，爆源-自由场模型与爆源-介质-结构整体计算模型中对应位置处的网格划分和材料属性应保持一致。

图2 二维爆源-自由场有限元模型示意图Fig.2 The 2D source-free field finite element model

(1)

(2)

式中，上标0表示自由波场。

对于自由场模型，当应力波通过子结构区域后，可以认为再无反射波进入内部区域，此时假设内部区域节点处于静止状态，即

uC=0,uI=0

(3)

将式(3)代入式(2)，得到

(4)

图3 二维爆源子结构模型Fig.3 The 2D substructure model of explosion source

爆源子结构的运动方程可以写成如下形式

(5)

式中，上标S表示子结构模型。根据有限元理论，若子结构模型的网格尺寸和材料属性与自由场模型相应位置处完全一致，那么以下关系成立

(6)

(7)

以上推导得到的爆源子结构方法可利用较小的计算成本获得近爆源场地的等效爆炸荷载。需要说明的是该方法是基于有限元理论推导得到的，其计算精度由有限元理论支撑。对于爆炸荷载等强冲击、短持时的荷载形式，有限元显式时域逐步积分理论中有明确的关于稳定性条件要求，无阻尼和有阻尼情况下，稳定极限分别如下：

无阻尼稳定极限

(8)

有阻尼稳定极限

(9)

式中：ωmax为系统最高频率；ξ为最高频率模态的临界阻尼部分。在实际研究过程中，稳定性条件也可使用以下定义[28]

(10)

式中：Le为模型最小单元尺寸；CP为材料压缩波速。计算前可利用上式估算满足稳定性条件的临界时间步长。

2 基于爆源子结构的多尺度分析方法

在近爆源区域，由于炸药释放能量的时间极短，爆轰产物和周边介质的动力相互作用极为复杂，即便计算步长满足稳定性条件，计算结果也会随网格尺寸发生较大变化。一般认为近爆源区域的网格密度越大，计算精度越高。为获得更加精确的计算结果，需要在爆源子结构的基础上，对近爆源区域的网格进行加密处理，加密后的爆源子结构局部见图4。

图4 二维爆源自由场单元加密模型局部图Fig.4 Local diagram of the 2D source-free field model with high-density mesh

对网格加密后的近爆源区域进行动力计算，可获得较为精确的爆炸自由场运动，将爆源子结构所对应的节点位移数据从小尺度的近爆源区域自由场模型中提取出来，再施加到大尺度爆源子结构模型上，通过动力分析获得等效爆炸荷载。

以上即是多尺度分析的实现方法。需要注意的是，近爆源区域的动力计算是在小尺度的网格上进行的，而爆源子结构是大尺度网格模型，因此在近爆源自由场提取节点位移时，不需遍历子结构区域对应的所有节点，而是在节点群中“跳跃”式地间隔提取，此操作大幅降低了需要处理的节点数据。随后再将提取的位移数据一一施加于爆源子结构的对应位置处，通过动力计算获得大尺度场地-目标模型中的等效爆炸荷载。这种处理方法既体现了多尺度分析的思想，又具有两点优势：一是通过“跳跃”式地采集和加载位移数据实现了网格尺度过渡，避免了采用不规则形状单元的传统网格过渡方式，既降低了建模难度，又提高了计算精度。二是在有限元理论中，排除网格尺度效应影响。节点位移的提取和加载与单元尺寸无关，而节点力则与单元尺寸相关。本文正是利用了节点位移这一不受网格尺寸影响的物理量，通过爆源子结构将其转化为节点力，从而保证大尺度场地-目标模型的计算精度。

另外，本文网格尺寸过渡的对象是近爆源区域的拉格朗日网格。利用流固耦合算法对近爆源区域进行数值计算时，需要在炸药和释放爆轰产物区域划分欧拉网格。为保证计算精度，欧拉网格的尺寸一般要小于或等于拉格朗日网格。在近爆源区域，拉格朗日和欧拉网格可能互相重叠。由于欧拉网格节点没有位移运动，在提取自由场运动数据时需要注意区分。

3 具体操作流程

爆炸问题的多尺度分析方法的核心思想是利用爆源子结构理论，将近爆源区域的场地运动转化为等效爆炸荷载，同时实现由小尺度网格至大尺度网格的网格尺寸过渡。该方法的操作流程如图5所示，具体步骤如下：

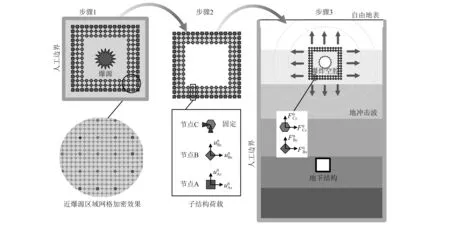
图5 二维爆源子结构多尺度方法流程图Fig.5 The implementation steps of the 2D multiscale method based on the explosion source substructure

步骤1建立近爆源区域的爆源-自由场小尺度模型，模型四周均设置人工边界条件。根据计算精度要求和稳定性条件进行网格划分，开展动力计算，提取场地运动的时程数据，即节点A(■)和节点B(◆)的位移时程数据(速度时程或加速度时程亦可)。

4 算例验证

4.1 均匀半空间自由场算例

首先利用二维自由场算例对本文方法的有效性进行验证，二维模型如图6所示，长宽均为500 m，炸药尺寸为0.4 m×0.4 m，炸药的几何中心位于埋深100 m处，模型两侧和底部设置二维黏弹性人工边界单元。自由场介质参照常用土壤进行参数设置，密度取为2 000 kg/m3，剪切波速为300 m/s，泊松比为0.3。选取A、B、C和D点观察计算结果。

图6 二维均匀半空间自由场模型Fig.6 The 2D homogeneous half-space free field model

利用基于爆源子结构的多尺度方法计算整体模型的动力反应时，首先要考虑如何截取近爆源区域。近爆源模型爆炸反应计算需要模拟爆炸波在全无限空间中的辐射，一旦人工边界的计算精度不够，外行爆炸波场到达截断边界时会产生反射波，直接导致自由波场运动出现误差，对后续计算分析影响较大。黏弹性人工边界单元是利用单元矩阵等效原理构造等效单元来模拟黏弹性人工边界，而黏弹性人工边界是基于柱面波和球面波理论推导的，在弹性波场中具有较高的计算精度。因此，应尽可能将人工边界设置在弹塑性区和弹性区的交界处，在降低计算成本的同时，又可保证获得较为准确的计算结果。本算例截取的近爆源区域的尺寸为60 m×60 m，炸药位于近爆源区域的几何中心。近爆源区域模型如图7所示。

图7 二维近爆源区域模型图Fig.7 The 2D near-source area model

首先利用通用有限元软件LS-DYNA的流固耦合算法对近爆源区域进行动力反应计算。近爆源区域模型采用小尺度网格离散，炸药和空气采用Eulerian单元，网格尺寸4 cm×4 cm，土壤采用Lagrange单元，网格尺寸5 cm×5 cm。土壤介质的本构模型采用带失效的土壤和可压缩泡沫塑料模型(soil and foam)，该本构模型可以模拟土体大变形和失效行为。土体材料的力学参数为(单位制cm，g，us)：密度2.0，剪切波速0.03，弹性模量0.004 8，剪切模量0.001 8，泊松比0.3。TNT炸药采用高爆炸药材料模拟，该材料利用炸药的爆轰速度、CJ(chapman-jouguet)面压力等材料性质，联合状态方程确定一定当量炸药在周围介质中形成的爆炸冲击波压力。主要参数为(单位制cm,g,us)：密度1.64，爆轰速度0.693，爆轰波阵面压力0.27。炸药爆轰产物状态方程采用JWL状态方程，具体参数为(单位制cm，g，us)：单位体积炸药内能0.07，A=3.14×10-2，B=3.23×10-2，R1=4.15，R2=0.95，ω=0.3。在空气模型中，通过块体单元，采用空材料和线性多项式状态方程来模拟炸药爆炸产物流动的空腔，进行多物质流固耦合处理[29-31]。

爆源子结构取为正方形，其各边至炸药中心的距离为1 800 cm。子结构及不含爆源的自由场模型采用大尺度网格离散，网格尺寸为90 cm×90 cm。选择爆源子结构外层节点M和节点N、中间层节点P和节点Q观察近爆源自由场的运动。

此外，为验证本文方法的准确性，建立考虑爆源的自由场整体模型。为准确模拟爆炸过程及爆炸冲击波在近爆源区域的传播，采用小尺度网格对整体模型进行有限元离散，网格尺寸与多尺度方法中的近爆源区域一致，为5 cm×5 cm。

图8给出了M点、N点、P点和Q点的竖向位移时程曲线。炸药起爆后，自由场运动在0.2 s左右到达峰值，此后地冲击应力波开始回落，由于爆炸空腔和塑性区影响，存在一定程度的残余位移。

图8 M、N、P和Q点位移时程曲线Fig.8 The displacement history curves on nodes M,N,P,Q

固定爆源子结构模型内侧一周的全部节点，将自由场运动的位移时程施加到子结构最外侧和中层节点上，计算内侧和中层节点的反作用力。图9给出了子结构内侧节点S和节点T、中间层节点P和节点Q的竖向反作用力时程曲线。

图9 P、Q、S和T点竖向节点反力时程曲线Fig.9 The history curves of the vertical reaction forces on nodes P,Q,S,T

将爆源子结构内侧和中间层节点的反力时程数据施加到不含爆源的自由场大尺度模型的对应位置处，计算自由场模型的动力反应。图10比较了采用基于爆源子结构的多尺度方法和整体方法计算得到的位移波场快照。

图10 多尺度方法和整体模型计算结果比较Fig.10 Comparison of the results calculated by the multiscale method and the overall model

从对比结果可以看出，当采用基于爆源子结构的多尺度方法进行计算时，自由波场从子结构所在位置开始向外传播，到达截断边界时，波场能量被人工边界单元有效吸收。由于多尺度方法没有考虑爆腔对波场运动的影响，自由表面反射波从子结构区域自上而下直接穿行，但从位移云图上看，此现象并没有对计算结果造成较大影响。为进一步比较多尺度方法的计算精度，图11对自由场模型中A、B、C和D点的位移时程数据进行比较。计算结果表明，对于自由场模型，基于爆源子结构的多尺度方法的计算结果与整体模型的计算结果吻合良好。

图11 多尺度方法和整体模型计算的节点位移比较Fig.11 Comparison of the nodal displacements calculated by the multiscale method and the overall model

4.2 成层半空间自由场算例

进一步验证本文方法对于成层半空间场地的适用性。算例模型沿竖向分为三层，上层介质的密度为2 000 kg/m3，剪切波速为300 m/s，泊松比为0.3；中层介质的密度为2 500 kg/m3，剪切波速为500 m/s，泊松比为0.27；下层介质的密度为2 700 kg/m3，剪切波速为800 m/s，泊松比为0.26。近爆源区域以及其余模型参数均与均匀半空间算例相同。选取A、B、C和D点观察计算结果。具体模型和观测点位置如图12所示。

图12 二维成层半空间自由场模型Fig.12 The 2D layered half-space free field model

根据多尺度分析步骤，先建立与上节算例相同的近爆源区域小尺度模型，获得近爆源自由场运动，随后建立爆源子结构模型，施加节点位移时程后，通过动力计算获取节点的反作用力，再施加到对应的成层自由场大尺度模型的相应位置处。

图13比较了多尺度方法和整体方法计算得到的位移波场快照。自由波场从子结构所在位置开始向外传播，到达自由表面处发生反射，到达介质分层处同时发生反射和折射，到达截断边界位置被人工边界单元吸收。自由表面和分层界面的反射波均在子结构内部通过，从位移云图上看，同样没有对计算结果造成较大影响。

图13 多尺度方法和整体模型计算结果比较Fig.13 Comparison of the results calculated by the multiscale method and the overall model

为进一步分析本文方法对于成层介质情况的计算精度，对A、B、C和D点四个观测点的位移时程数据进行比较。如图14所示。

图14 多尺度方法和整体模型计算的节点位移比较Fig.14 Comparison of the nodal displacements calculated by the multiscale method and the overall model

计算结果表明，多尺度方法的计算结果同样具有较高精度。表1给出多尺度方法和整体模型计算效率的比较。多尺度方法的单元数量比整体模型少95.9%，计算时间减少88.4%，在满足计算精度的前提下，多尺度方法的计算效率优势明显。

表1 多尺度方法和整体模型计算效率比较Tab.1 Comparison of the computational efficiency between the multiscale method and overall model

5 结 论

针对大当量爆炸荷载作用下的大范围工程场地有限元模型动力计算问题，本文发展了一种基于爆源子结构的多尺度分析方法。该方法在完成爆炸波场转换的同时，实现网格尺度过渡，从而将大范围场地整体模型拆分，由近至远逐步完成动力计算分析。通过二维算例验证了本文方法的可靠性。本文主要结论如下：

(1)本文提出的基于爆源子结构理论的爆炸荷载多尺度计算方法克服了整体模型单元数量多，计算成本高等问题，不仅具有较高的计算精度，且大幅提高了计算效率。

(2)就多尺度方法本身而言，第一步近爆源自由场地动力计算是耗时最多的。但在炸药当量给定的情况下，该步计算结果可作为标准荷载，对于不同模型，或是相同模型分析不同位置爆炸时，均可以重复使用，节省大量计算时间。

(3)连续介质波动问题的多尺度分析中，一般采用不规则单元进行网格过渡，这会对计算精度产生一定影响。本文多尺度方法利用爆源子结构实现网格过渡，避免了不规则单元的出现，保证了计算精度。

此外，本文方法在计算过程中涉及大量节点空间信息比对和时程数据的读写，手工操作效率低且极易出错，影响该方法的实用性。本文通过自编程序对限元软件进行二次开发，利用计算机在较短时间内自动完成模型建模和后处理等工作，极大提高了工作效率，对多尺度方法的推广应用有重要意义。