深度概率优化的VAE轴承状态评估

尹爱军，陈小敏，谭 建，王 昱

(1.重庆大学 机械传动国家重点实验室，机械工程学院，重庆 4000442.中国石油西南油气田分公司重庆气矿，重庆 400021)

轴承是通用机械中最常用的组件之一[1]，其工作状态影响了各领域机械的寿命、性能、可靠性等。研究轴承的性能退化特征，建立其状态评估模型是提升机械设备可靠性的关键。针对轴承状态评估模型的建立，目前已有不少研究方法[2-6]。刘国增等[7]将小波包AR能量熵与平滑样条方法相结合用于判定轴承的退化状况。张小强等[8]基于人工免疫算法优化离散隐马尔科夫模型，以提高故障诊断精度。刘美芳等[9]融合贝叶斯推论和自组织映射，提出了基于负对数似然概率的轴承性能退化评估指标。Pavle等[10]提出了一种基于Renyi熵的轴承故障预测方法。在现有的轴承状态评估方法中，基于振动信号分析的评估模型需人为提取特征，但由于噪声及非监测部位的干扰，所提取的特征往往不够全面；基于数据驱动机器学习的状态评估模型存在着评估效果依赖模型参数程度高、对轴承早期故障不敏感、过度拟合等问题。

变分自编码器(variational auto-encoder，VAE)提出的优化算法及易优化的随机梯度评估器使其在训练小批量样本上具备高效性，且无需人为提取数据特征。目前，VAE已经成为最流行的无监督学习方法之一[11]，被广泛应用在人脸图像生成[12]、手写数字生成[13]、语义分割[14]等方面。在机械故障检测中，马波等[15]以VAE变分证据下界表征出压缩机组振动信号特征的分布模型，实现压缩机组的故障预警，但当样本容量大于600组时，该方法对压缩机组异常状态的敏感性降低。由于VAE后验分布的简化高斯假设以及通过优化变分证据下界(evidence lower bound,ELBO)实现最大化边缘概率密度，导致边缘概率分布的估算值与真实值之间存在一定误差，且当样本容量过大时，对异常数据的敏感度较低。

构造丰富灵活的近似后验分布有助于提高模型性能以及提供可靠的置信区间。已经尝试通过使用自回归将近似后验视为条件分布链分解的方法来改善近似后验分布[16]。但由于真实后验分布的复杂度，上述方法仍具有局限性。基于深度概率优化(deep probability optimization，DPO)，考虑将分布变换引入VAE，通过构造灵活复杂的近似后验分布来逼近真实后验分布。本文采用标准化流(normalizing flows，NF)完成分布变换过程，标准化流利用一系列可优化的可逆映射，将原始分布转换为任意复杂分布，可用于强化学习、变分推断、生成模型等。如Salman等[17]提出了深度微分同态标准化流模型，能有效实现似然评估和灵活的密度估计。通过Normalizing Flows改进VAE，很大程度上能捕获真实后验分布。但VAE的边缘概率密度值仍难以直接准确估算，一般通过对数似然估计器核密度估计法(Kernel Density Estimation，KDE)来实现。但KDE由于先验分布和真实后验分布有着较大差异，在高维数据中估计的准确率较低。考虑通过优化采样算法优化边缘概率密度计算过程，其中退火重要性采样(annealed importance sampling，AIS)在估计基于解码的生成模型的概率分布中，有着较高的准确率，主要应用在估计状态期望以及归一化常数等方面[18],如Wu等[19]基于AIS实现手写数字图像的识别。

本文将分布变换引入到VAE中并融合优化采样算法，提出面向振动信号频谱特性的VAE-DPO轴承健康状态评估模型，该模型以频谱的边缘概率密度作为轴承健康评价指标。基于深度概率优化，针对VAE后验分布的简化高斯假设，利用分布变换优化近似后验分布，并通过Normalizing Flows实现，NF运用可优化的双射变换来构造丰富灵活的近似后验分布，最后利用优化采样算法中的AIS实现边缘概率密度的优化计算。通过滚动轴承状态评估实例验证了该模型在轴承状态评估中的有效性及良好的早期敏感性。

1 VAE

VAE有向概率图如图1所示。实线为生成模型pθ(z)pθ(x(j)|z)，虚线表示近似后验分布qφ(z|x(j))到真实后验分布pθ(z|x(j))，N表示推断的次数。

图1 VAE有向概率图Fig.1 Directed probability chart of VAE

VAE试图通过训练将生成的每个x(j)的概率最大化x(j)，即极大化概率密度函数pθ(x(j))的似然概率：

(1)

式中：指定先验分布pθ(z)=N(z;0,I)，I为单元阵，Ez～pθ(z)[pθ(x(j)|z)]表示pθ(x(j)|z)的期望。VAE利用衡量两分布之间差异程度的KL散度，将优化目标极大化lgpθ(x(j))转为极大化变分证据下界函数L(θ,φ;x(j))：

L(θ,φ;x(j))=Εz～qφ(z|x(j))[lgpθ(x(j)|z)]-DKL[qφ(z|x(j))‖pθ(z)]

(2)

式中：-Εz～qφ(z|x(j))[lgpθ(x(j)|z)]表示重构误差，DKL[qφ(z|x(j))‖pθ(z)]为KL散度损失，且qφ(z|x(j))=N(z;μ(j),(σ(j))2)。为解决参数φ在L(θ,φ;x(j))中不便于梯度计算的问题，VAE用辅助噪声变量ε～N(0,I)实现重参数化技巧，即z=μ+σε。

2 基于VAE-DPO的轴承健康评估

2.1 深度优化VAE近似后验分布

VAE变分推断中，近似后验分布简化为高斯分布，一般的高斯分布无法拟合足够复杂的后验分布。通过分布变换构造复杂灵活的VAE近似后验分布，改进后的VAE有向概率图如图2。经过一系列链式分布变换，初始近似后验分布变换的更加复杂，能有效逼近真实后验分布，初始分布下的隐变量Z0被映射为Zk。其余部分与图1概念相同。

图2 VAE近似后验分布深度优化后有向概率图Fig.2 Directed probability chart after deep optimization of VAE approximate posterior distribution

本文应用Normalizing Flows完成分布变换过程，标准化流通过参数化的可逆变换构造复杂灵活分布。

经由K次链式非线性变换序列f(z)=z+uh(wTz+b)，任意初始分布q0(z0)转化为任意复杂连续分布qK(zK)：

zK=fK°…°f2f1(z0)

(3)

其中λ={w∈d,u∈d,b∈d}是需要学习的自由参数，h(·)是连续的非线性映射[20]。初始随机变量z0变换为最终变量zK。

将Normalizing Flows运用于变分推断，使用长度为K链式映射f(z)，近似后验分布qφ(z|x(j))变换为更灵活的qK(zK)。初始分布q0(z0)=q0(z0|x(j))仍是简单高斯分布N(z;μ(j),(σ(j))2)，利用深度神经网络建立从观测数据X到初始分布q0(z0)的参数以及λ参数的映射。Normalizing Flows改写式(2)变分证据下界，且转换为在初始分布q0(z0)上的期望：

L(θ,φ;x(j))=Eqφ(z|x(j))[lgpθ(x(j),z)-lgqφ(z|x(j))]=

(4)

Normalizing Flows改进VAE，获得灵活丰富的近似后验分布，且仅需要对VAE做极小修改。

2.2 基于AIS的VAE边缘概率密度评价指标

由于边缘概率密度p(x)难以直接计算，因此基于变分自编码器的机械设备状态评估方法通常将变分证据下界L(θ,φ;x(j))作为机械设备健康状态指标。然而直接以变分证据下界为优化目标，模型性能不理想，且可能造成优化前后的先验分布差异较大。为优化观测数据x边缘概率密度的计算，利用KDE、AIS等方法。但KDE无一系列中间过渡分布，在高维数据估计中准确率较低。AIS将一系列中间分布逐渐转变为目标分布，通过马尔科夫链跃迁进行退火序列，定义重要性采样，获得后验分布样本，实现对边缘概率密度的优化计算。

基于退火算法，设r0(z)=p(x,z)为目标分布，VAE先验分布p(z)为AIS初始采样分布ri(z)，定义中间分布：

ri(z)=p(z)p(x|z)βi

(5)

式中：0=βn<βn-1<…<β1<β0=1，βi单调递增。设一系列分布gn，…g0，gi与ri成比例，且从gn采样能生成一系列独立的点。指定可逆马尔可夫蒙特卡洛(MCMC)状态转移矩阵Ai(z,z′)，要求保持gi不变。基于AIS的p(x)估计从初始分布gn采样一个初始状态zn-1，并利用状态转移矩阵Ai不断采样下一个状态，采样的状态zi服从中间分布ri。根据马尔科夫链性质，一系列平滑的采样产生一系列点zn-1，zn-2，…z1，z0，从而得到权重:

(6)

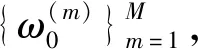
(7)

2.3 VAE-DPO轴承状态评估模型

人为提取振动信号特征会造成信息量的损失，而信号频域幅值谱在欧式空间具有更为稳定的概率分布，本文采用振动信号幅值谱作为观测数据。所提出的基于深度概率优化的评估模型通过建立振动信号频谱的贝叶斯概率推断模型并利用分布变换优化分布，通过优化采样算法对振动信号频谱高维空间中真实复杂概率分布的精确逼近，实现对振动信号状态的定量评估。

VAE-DPO轴承健康状态评估模型流程如图3所示。

图3 VAE-DPO轴承健康状态评估流程Fig.3 VAE-DPO bearing condition evaluation process

1)为降低原始信号数据规模，并避免信息量的损失，将振动信号时域信号转换为频域信号X(f)。根据轴承退化规律，轴承服役过程为缓慢退化过程，在运行初期其振动特性基本不变[21-22]。因将样本数据前期阶段作为训练集用于学习健康状态模型，测试集为所有样本数据。

2)输入训练集数据XA(f)，训练并优化VAE模型参数，其中利用Normalizing Flows优化近似后验分布。

3)输入测试数据集振动信号全频谱X(f)，传入训练完毕且分布优化后的VAE，并保存p(z)、p(x|z)参数。

4)接着AIS从p(z)中采样初始值，利用接受-拒绝采样方法实现中间分布样本采样，通过一系列中间分布过渡到目标分布。由AIS权重期望值优化计算轴承健康评价指标p(x)，实现轴承健康状态评估。

在运行的前期阶段轴承处于正常状态，如图3中x振动信号频谱图A阶段。因此，A阶段振动信号频谱作为训练集，学习建立健康状态模型。即输入XA(f)后，使用Adam梯度优化算法获取轴承健康状态下引入分布变换后VAE的最优参数。在测试阶段，将数据X(f)输入改进后的VAE模型，并保存相关参数后，AIS利用Metropolis-Hastings采样样本并同时以几何平均形式的转移中间分布过渡到目标分布。计算权重的期望从而精确估计健康评价指标p(x)，完成优化计算过程，实现轴承健康状态定量评估。

3 对比实验

为验证VAE-DPO模型及所提健康评估指标对轴承状态评估的有效性，采用Cincinnati大学IMS实验室开源滚动轴承加速退化实验的实验数据进行对比实验[23]。试验台转速恒为2000RPM。采用加速度传感器分别采集4个轴承振动信号数据，其中采样频率为20 kHz，每隔10 min采集一次。历时9 840 min，轴承1出现故障，停止试验。VAE模型具体参数设置如表1。

表1 VAE模型参数设置Tab.1 Parameters setting up of VAE

轴承1在运行9 840 min后出现外圈故障，利用其全寿命数据验证所提方法的有效性。轴承振动信号时域特征随时间变化趋势及与VAE-DPO模型对比如图4。为使评估结果对比清晰，利用1减去归一化处理后的评估指标值。由时域特征退化曲线知，在轴承前期阶段曲线保持稳定，可以认为轴承在前4 500 min未出现退化。因此，在模型训练阶段采用前1 000 min数据，利用VAE学习建立轴承健康状态模型；振动信号全频谱数据为测试集，由此得到基于VAE-DPO模型的健康评估结果。

由图4可以看出，VAE-DPO状态评估趋势与振动信号有效值、方根幅值一致，表明该模型的准确性，能很好的表征出滚动轴承退化状况的规律。相对有效值、方根幅值，VAE-DPO提早1 800 min产生变化，在约5 190 min时，曲线发生明显上升走向。表明VAE-DPO相对传统特征参数，能更早发现轴承早期退化状态。

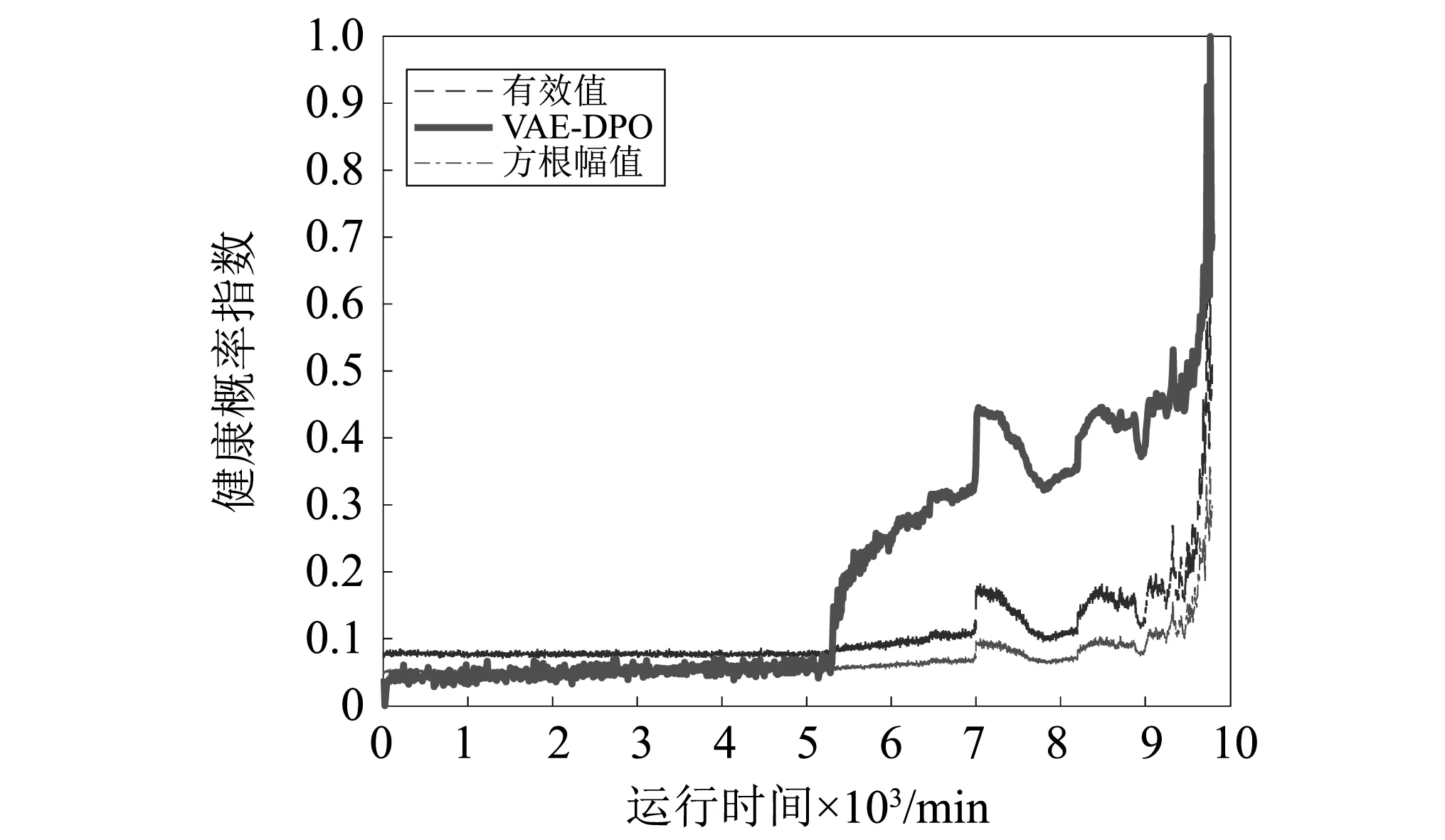
图4 VAE-DPO与传统健康模型评估结果对比Fig.4 Comparison of VAE-DPO and traditional health model evaluation results

为验证分布变换后的VAE近似后验分布更加灵活复杂，能表征真实的隐变量空间，比较Normalizing Flows改进VAE模型前后的变分证据下界[24]。由轴承1时域特征变化趋势，将轴承运行全过程前4 200 min设为健康状态，并取ELBO均值，退化时期选取5 190 min时刻对比，如表2。其中FVAE表示NF优化后的VAE模型。

表2 变分证据下界比较Tab.2 Comparison of the evidence lower bound

VAE在健康状态时ELBO值越大模型性能越好，在退化时期隐变量逐渐偏离原始分布，ELBO值降低。表2所示，FVAE的变分证据下界值在健康状态时高于VAE，而在退化时期低于VAE。说明将分布变换引入VAE后，通过优化分布改善了模型性能，能更有效的通过隐变量学习轴承振动信号频谱潜在特征。

VAE-DPO、FVAE-KDE、VAE和VAE-AIS状态评估方法效果对比如图5所示。深度信念网络DBN(Deep Belief Networks)、隐马尔科夫HMM(Hidden Markov Model)、长短期记忆网络LSTM(Long Short-Term Memory)[25]与VAE-DPO模型评估结果如图6所示。

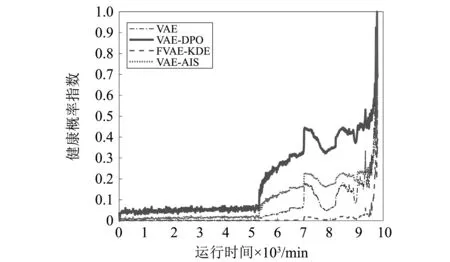
图5 VAE-DPO、FVAE-KDE、VAE和VAE-AIS状态评估结果对比Fig.5 Comparison of VAE-DPO、FVAE-KDE、VAE and VAE-AIS evaluation results

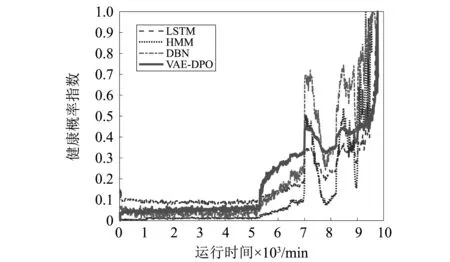
图6 VAE-DPO、HMM、DBN和LSTM状态评估结果对比Fig.6 Comparison of VAE-DPO、HMM、DBN and LSTM evaluation results

为量化各模型对轴承早期故障的检测性能，利用原则分别计算各模型轴承退化状态在前4 200 min的健康状态评估指标上界，超过此值即认为轴承进入早期退化时期，由此确定各模型发现轴承初始退化状态时的时间，如表3所示。

表3 各模型早期退化状态评估性能Tab.3 Early degradation state assessment performance of each model

图5、图6及表3表明，VAE在5 310 min时产生轻微变化，上升趋势较平稳，说明VAE模型直接以变分下界为评估指标对轴承异常工况的敏感度较低。FVAE-KDE评估曲线在5 360 min时才发生突变，对轴承退化状态较不敏感，尤其是轴承早期故障。说明AIS比KDE方法更能准确估计边缘概率密度。VAE-DPO比VAE-AIS模型早10分钟进入早期退化时期，且在轴承由健康状态进入早期退化阶段曲线表现出明显突变。表明NF通过优化近似后验分布达到改进VAE模型的目的。HMM和LSTM分别在5 320 min和5 370 min时才缓慢出现上升，虽然DBN在5 310 min时有较明显的上升趋势，但VAE-DPO在5 190 min便出现突变，曲线变化率明显高于各个模型。表明VAE-DPO对于轴承早期退化状态的敏感性均强于FVAE-KDE、VAE-AIS、VAE、HMM、DBN、LSTM。

图7、图8分别为轴承2、轴承4的退化对比实验图，各模型量化的初始退化时间如图9所示。

图7 轴承2的VAE-DPO、HMM、DBN和LSTM状态评估结果对比Fig.7 Comparison of VAE-DPO、HMM、DBN and LSTM evaluation results of bearing 2

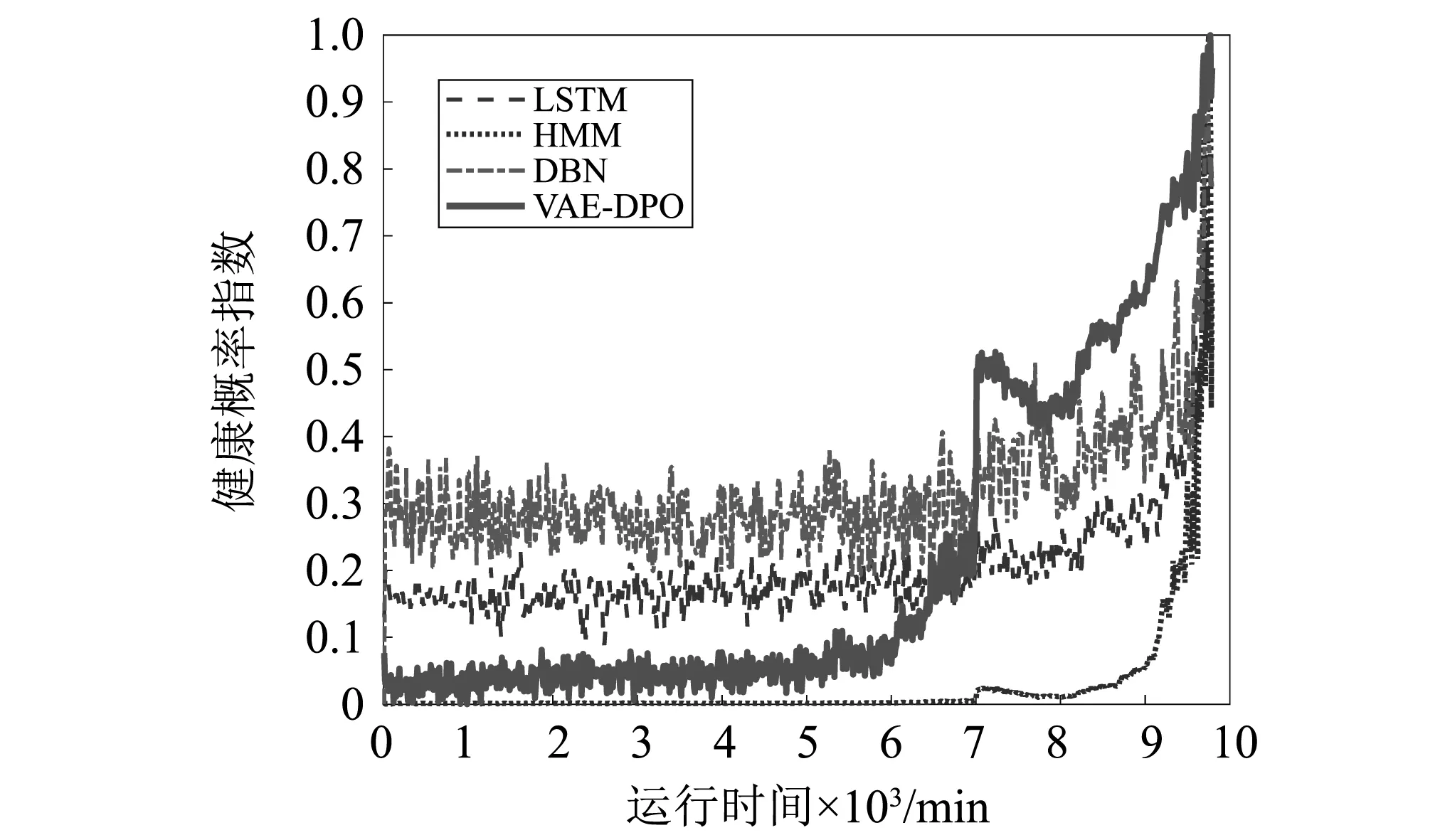
图8 轴承4的VAE-DPO、HMM、DBN和LSTM状态评估结果对比Fig.8 Comparison of VAE-DPO、HMM、DBN and LSTM evaluation results of bearing 4

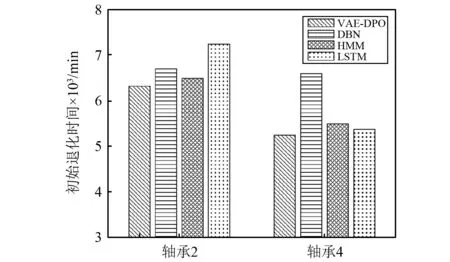
图9 轴承2、4的各模型早期退化状态评估性能Fig.9 Early degradation state assessment performance of each model of bearing 2 and 4

由图7～图9可知，对轴承2和轴承4，VAE-DPO模型同样对其早期退化状态更为敏感，且其曲线变化趋势更清晰的说明轴承退化过程。

4 结 论

尽早发现轴承退化状态，更易了解轴承故障的根本原因，有利于避免机械设备发生突发故障。本文基于深度概率优化，引入分布变换到VAE中并结合优化采样算法AIS构造VAE-DPO模型用于轴承健康状态评估，进而提出基于边缘概率密度的健康评价指标。VAE通过隐变量学习轴承振动信号频谱数据的概率分布，但因为后验分布的简化假设，限制模型的表达能力。采用分布变换，通过Normalizing Flows使用一系列可逆映射变换，使近似后验分布足够逼近真实后验分布，改善模型性能。由于边缘概率密度的计算复杂性，本文利用优化采样算法中的AIS优化计算振动信号边缘概率密度，实现轴承健康状态的评估。轴承退化对比实验表明，该模型充分发挥了VAE在提取振动信号频谱概率分布特征方面、Normalizing Flows构造灵活分布以及AIS通过采样估计函数期望和逼近目标分布的优势；且VAE-DPO模型无需人为提取特征及相关复杂参数的设置，避免提取特征时原始信号信息的损失，对早期退化也更为敏感，有效实现轴承退化状态的定量评估。

本文研究分布变换优化VAE近似后验分布，并采用标准化流实现；利用AIS获得后验分布样本，完成p(x)优化计算。选取的方法过于局限，后续研究将着重考虑更多的流式结构或网络结构应用在优化VAE近似后验分布中，以及其余似然估计方法用于p(x)的优化计算。