随机变量线性组合的分布的一个算法

张 新 赵书银 胡金江

（河北建筑工程学院数理学院，河北 张家口075000）

0 引 言

多个随机变量的函数的概率密度是概率论课程中计算较繁琐的部分.两个相互独立的连续型随机变量之和的概率密度，可以用卷积运算得到，而求解多个相互独立的随机变量的和的概率密度需要进行若干次卷积运算.本文利用傅立叶变换提供了一种算法，不仅可以计算多个相互独立的随机变量的和的概率密度，而且还能计算多个相互独立的随机变量的任意线性组合的概率密度.

1 主要结果

定理 设X1，X2，…，Xn是n个相互独立的随机变量，其概率密度分别为f1（x），f2（x），…，fn（x），随机变量，其中a1a2…an≠0，则Y的概率密度

2 定理的证明

为了证明这个结论，先证明三个引理.

引理1 设随机变量X的概率密度为f（x），则Y＝aX的概率密度为

证明 设a＜0，则Y的分布函数

从而

引理2 设随机变量X的概率密度为f（x），则Y＝X＋b的概率密度为

证明Y的分布函数

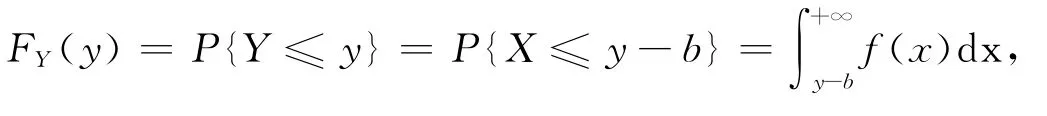
所以

引理3 设X1，X2，…Xn是n个相互独立的随机变量，其概率密度分别为f1（x），f2（x），…，fn（x），随机变量，则Y的概率密度

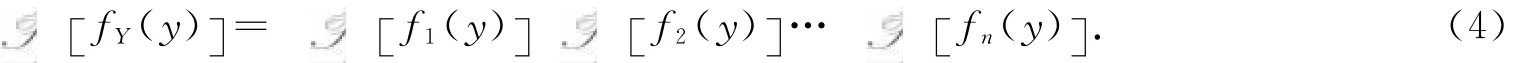
证明 当n＝2时，

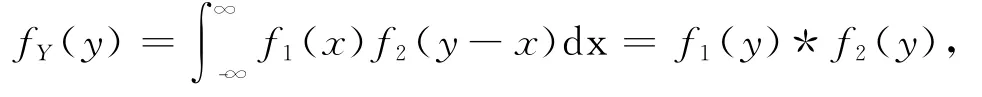
其中＊表示两个函数的卷积运算.由傅立叶变换的卷积性质，有

若结论对于n＝k时成立，则当n＝k＋1时，设，则Y＝Z＋Xn，由n＝2时的结果和n＝k时的结果，有

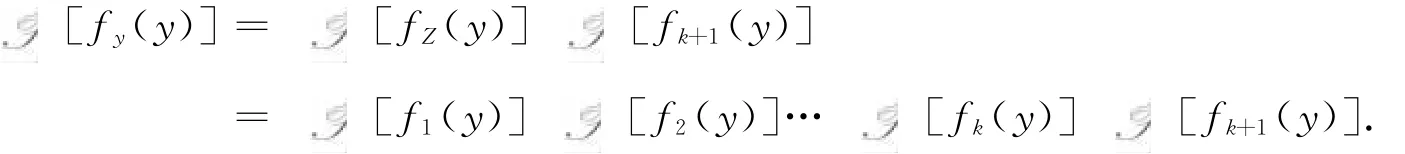
由归纳法假设即得（4）成立.

下面给出（1）式的证明.

设Yi＝aiXi，fYi（y）表示Yi的概率密度，fi（y）表示Xi的概率密度（i＝1，2，…，n），gn（y）表示Yn＋b的概率密度，则，于是.所以由引理3得

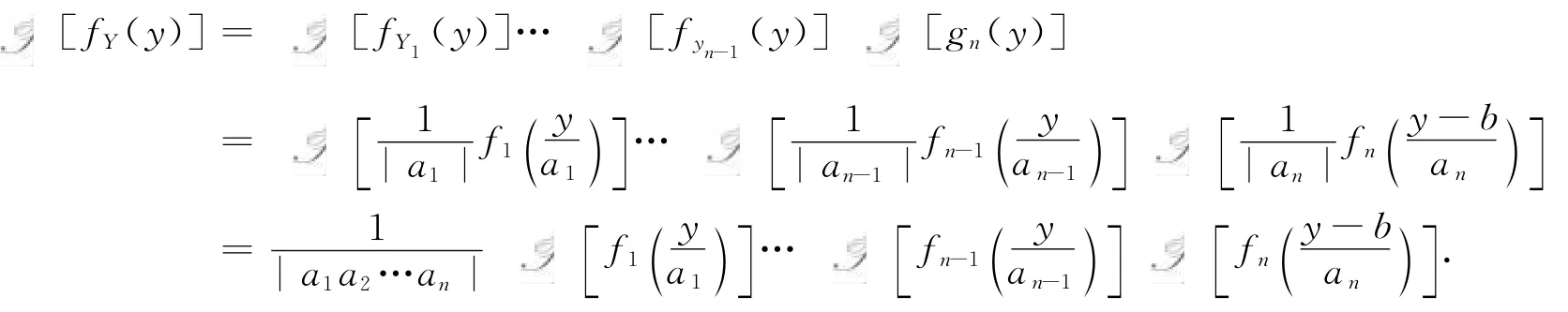
两边取傅里叶逆变换即得（1）式.

3 在中心极限定理的计算中的应用

以独立同分布的中心极限定理为例，设Xi具有相同的概率密度，则a1＝a2＝…＝，从而

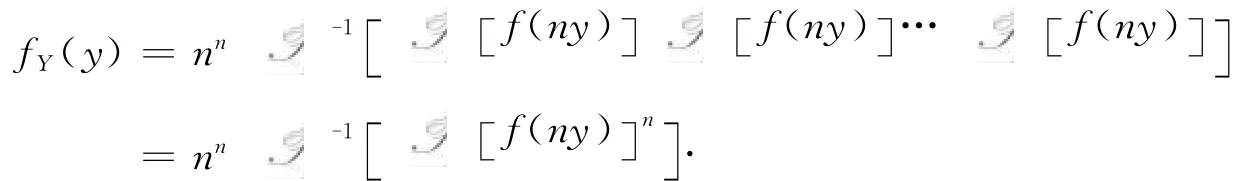
以Xi～E（1）为例，设它们相互独立，i＝1，2，…，n.则有

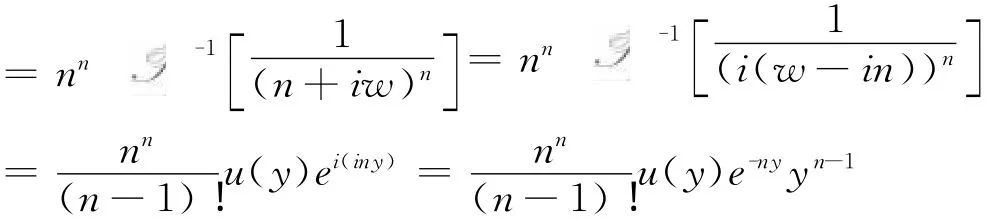
这里u（y）表示单位阶跃函数.

下图显示了当n＝5，30，100时，相互独立的参数为1的指数分布的随机变量之和的标准化变量的概率密度图像和标准正态分布的概率密度图像（虚线表示标准正态分布图像）：

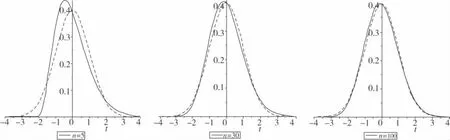
从图像上看，相互独立的指数分布之和的标准化变量收敛于标准正态分布的速度比较慢，当n＝100时二者图像仍然有明显的差距.

下图显示了当n＝3，5，14时，相互独立的U（0，1）分布的随机变量之和的标准化变量的概率密度图像和标准正态分布的概率密度图像（虚线表示标准正态分布图像）：

从图像上看，相互独立的均匀分布之和的标准化变量收敛于标准正态分布的速度比指数分布的情形要快，当n＝14时二者图像的差别就不明显了.

4 结 语

多个随机变量的函数的概率密度的计算量非常大.使用卷积计算时，即使使用计算机来实现，所用时间也不可忽视.笔者使用maple软件计算100个相互独立的指数分布随机变量的平均值，采用卷积和傅立叶变换法来计算，分别用时21.922秒和1.188秒，前者用时是后者的18.45倍，可见，傅立叶变换在随机变量函数的计算中是有优势的.但是因为傅立叶变换只能处理线性问题，也就是线性组合的情况，对于非线性的情形就无能为力了，当然卷积也处理不了非线性问题.

［1］张元林.积分变换（第四版）［M］.高等教育出版社，2003

［2］孙宏凯，李香玲，等.概率论与数理统计［M］.中国电力出版社，2009

［3］李贤平.概率论基础（第三版）［M］.高等教育出版社，2010

［4］张韵华.符号计算系统Maple教程［M］.中国科学技术大学出版社，2007