载荷变化时准双曲面齿轮副啮合参数演变分析

王笑乐，卢剑伟，杨士钦，谷先广

(1.安徽农业大学 工学院，合肥 230036；2.合肥工业大学 汽车与交通工程学院，合肥 230009；3.江淮汽车有限公司技术中心，合肥 230601)

掌握准双曲面齿轮副承载工况下的时变啮合参数是构建动力学模型时准确描述内部激励的重要前提[1-2]，也是评价其动态啮合特性的主要依据[3-5]。准双曲面齿轮相比圆柱齿轮具有更为复杂的齿面形貌和几何特征，难以采用如石川公式[6]、Weber能量法[7]等解析方法[8]计算轮齿应力应变，利用光弹性法[9]等试验测量目前也存在较大困难，有限元法是现阶段测算其承载啮合参数的主要技术手段。

国外有学者基于有限元法提出了螺旋锥齿轮啮合刚度的计算方法[10]，得到了沿齿高和齿长方向的位移曲线，未获得啮合刚度曲线。有学者将曲面积分与有限元法相结合对准双曲面齿轮进行加载接触分析[11]，得到其时变啮合参数，但是该方法中齿面接触区系人工设定，计算精度受接触区大小的影响。国内有学者基于有限元法计算了螺旋锥齿轮副单齿啮合刚度[12]，并线性叠加而得到多齿啮合刚度。由于螺旋锥齿轮齿面法向力方向具有时变特征，根据单齿刚度叠加计算多齿啮合刚度的准确度还需进一步验证。有学者基于有限元法结合中心差分法计算了准双曲面齿轮副等效啮合点位置、切线啮合刚度、等效啮合力[13]，不同工况下的传动误差及啮合刚度完整曲线未能给出。有学者计算准双曲面齿轮副无载、承载工况下的角传动误差来计算啮合刚度[14]，由于轮齿变形方向与齿轮旋转方向存在一定夹角，根据角传动误差计算啮合点变形量时存在一定近似。

现有研究中对轮齿啮合变形的计算通常采取线性叠加、部分提取或近似等效的方法，可能引起一定的误差。为此，本文基于准双曲面齿轮副LTCA分析结果，提取接触节点三维坐标、旋转半径及轮齿转角等参数，计算无载工况下接触节点由齿轮旋转产生的理论位移和承载工况下由轮齿旋转、接触、剪切、弯曲综合产生的实际位移，获得轮齿真实变形，并结合等效啮合力求得齿轮副时变啮合刚度。进一步考察载荷大小对啮合参数的影响，得到齿面啮合印痕、承载传动误差、实际重合度、等效啮合力、综合弹性变形、时变啮合刚度等参数随载荷变化的演变规律。

1 时变啮合参数的数学描述

1.1 等效啮合力

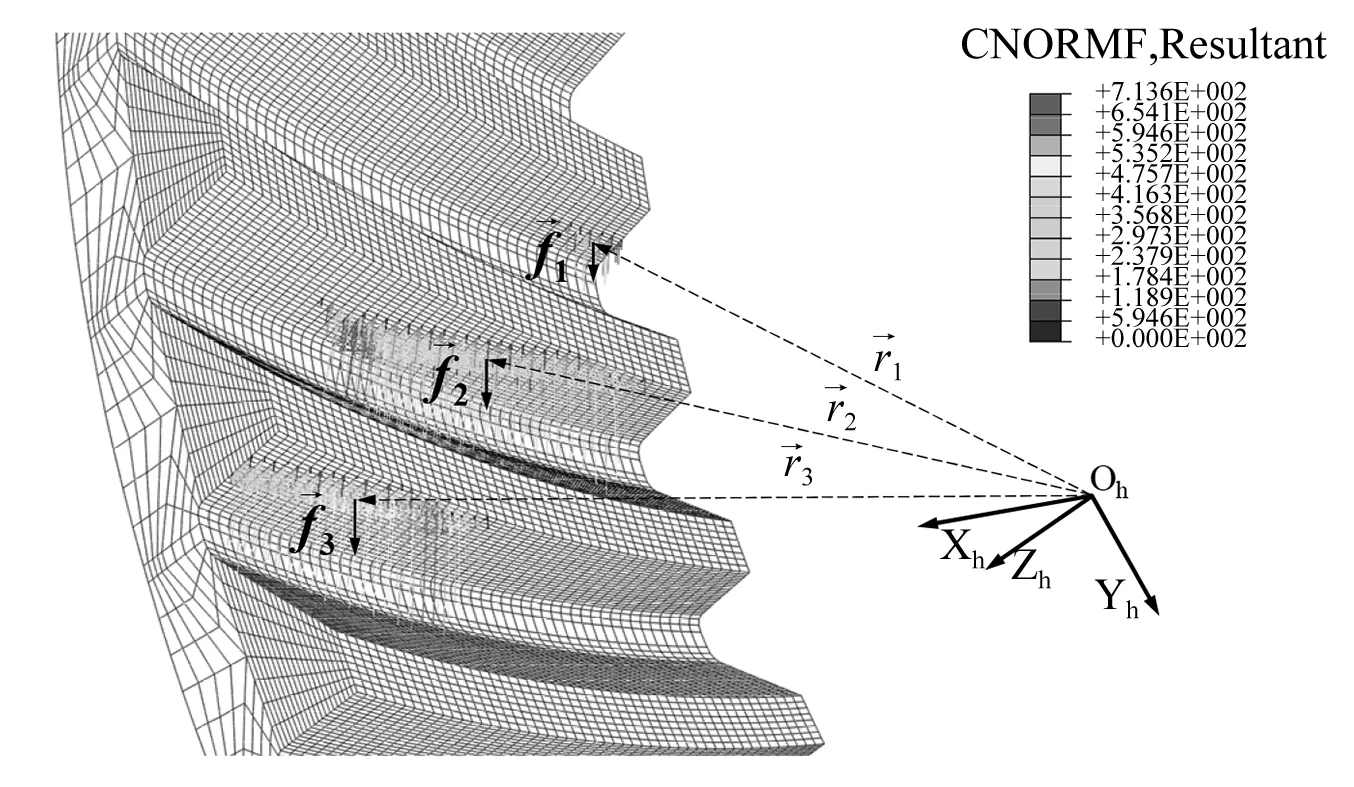
图1 等效啮合力及啮合力作用点Fig.1 Equivalent meshing force and its action points

(1)

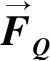
(2)

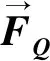
(3)

1.2 等效啮合点

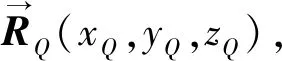
(4)

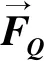
1.3 传动误差函数

准双曲面齿轮副啮合时为局部共轭点接触，传动比随齿轮转角不断变化，齿轮副存在传动误差，通常定义为小轮匀速回转时，大轮的实际转角与理论转角的差值，表达式为

(5)

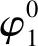
1.4 轮齿综合弹性变形

本文的研究对象为准双曲面齿轮副，在计算时将轴、轴承等结构视为刚体，忽略其变形对接触点位置的影响。轮齿的综合弹性变形可表示为

(6)

式中，uh，ub，us分别为齿面接触变形、轮齿弯曲和齿廓剪切变形，目前尚无解析公式计算上述三种变形。将式(6)变形为

(7)

轮齿综合弹性变形可通过分别计算大、小轮齿面接触点处三种形变共同产生的综合变形而得到。轮齿动态啮合时的真实位移由综合弹性变形和旋转位移叠加形成，如图2所示。图中大、小轮齿廓为啮合过程中t时刻，分别过大、小轮齿面上瞬时接触节点(图中大轮为点g，小轮为点p)的垂直于大、小轮各自旋转轴线的轴截面图，实际的大、小轮轴截面应相互交叉并垂直，此处采用轴截面图形式表示。

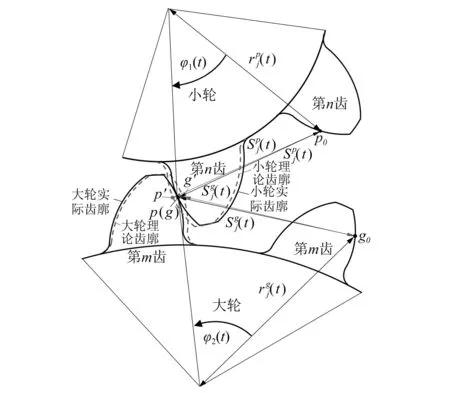
图2 齿面接触点处实际位移与理论位移Fig.2 Actual and theoretical displacements of the contacting points on tooth surfaces

图中点g0,p0表示在起始时刻对应于点g,p的点；点g′,p′表示假设大、小轮未啮合，由点g0,p0自由旋转至t时刻的点。|g0g′|,|p0p′|为点g0,p0自起始时刻至t时刻经自由旋转产生的理论位移。|g0g|,|p0p|为点g0,p0自起始时刻至t时刻经旋转和大、小轮接触变形而产生的实际位移。|g0g|-|g0g′|,|p0p|-|p0p′|为大、小轮实际位移与各自自由旋转产生的理论位移之差，即t时刻点g,p处的变形。|g0g|,|p0p|由点g0,p0处的自由旋转半径和从起始时刻至t时刻的旋转角度基于弦长公式计算；|g0g|,|p0p|由点g0,p0,g,p的三维坐标基于空间距离公式计算。

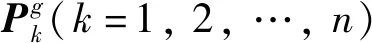
(8)

(9)

(10)

t时刻大轮综合弹性变形量可以表示为

(11)

小轮t时刻轮齿综合弹性变形的计算方法与大轮类似，则t时刻齿轮副的综合弹性变形为

un(t)=

(12)

h=1,2,…,l，l为t时刻小轮齿面接触节点总数，h为小轮齿面第h个节点，p为小轮。

1.5 时变啮合刚度

根据定义，t时刻齿轮副啮合刚度为

(13)

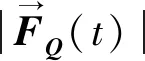
2 LTCA分析

2.1 齿轮副设计及加工参数

以一对刀倾半展成法加工的车用后桥主减速器准双曲面齿轮副为例，几何参数如表1所示，加工参数如表2，表3所示。大、小轮轴线分别与啮合坐标系z轴、x轴方向平行。

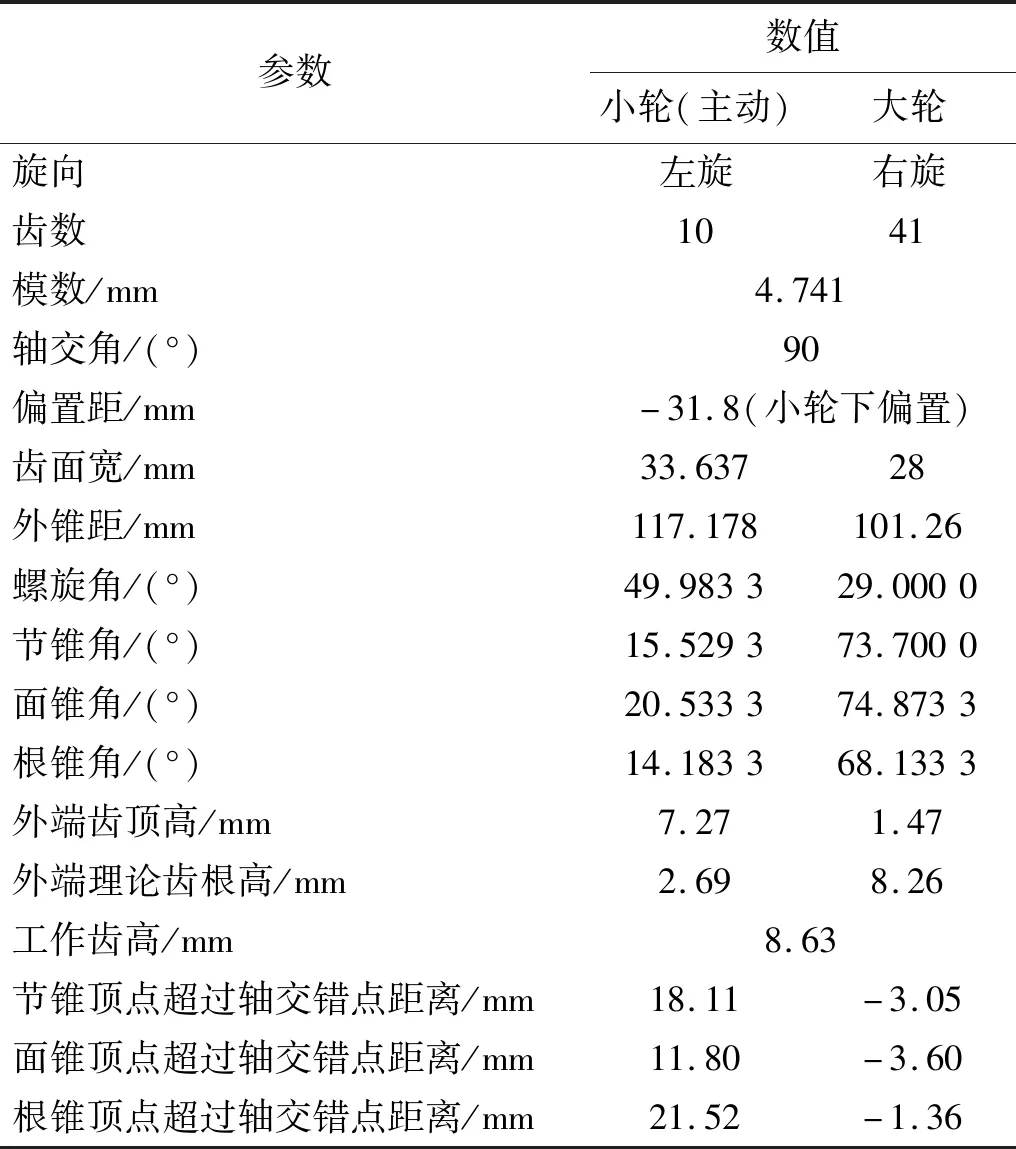
表1 准双曲面齿轮副几何参数Tab.1 Geometric parameters of the hypoid gear pair

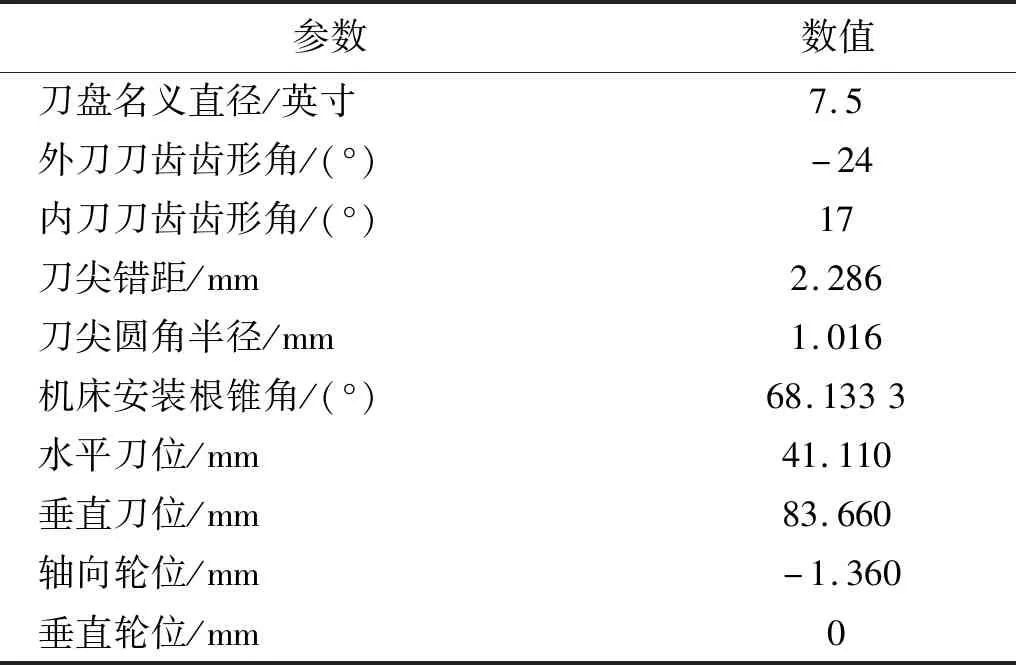
表2 大轮机床加工参数Tab.2 Machining parameters of the gear

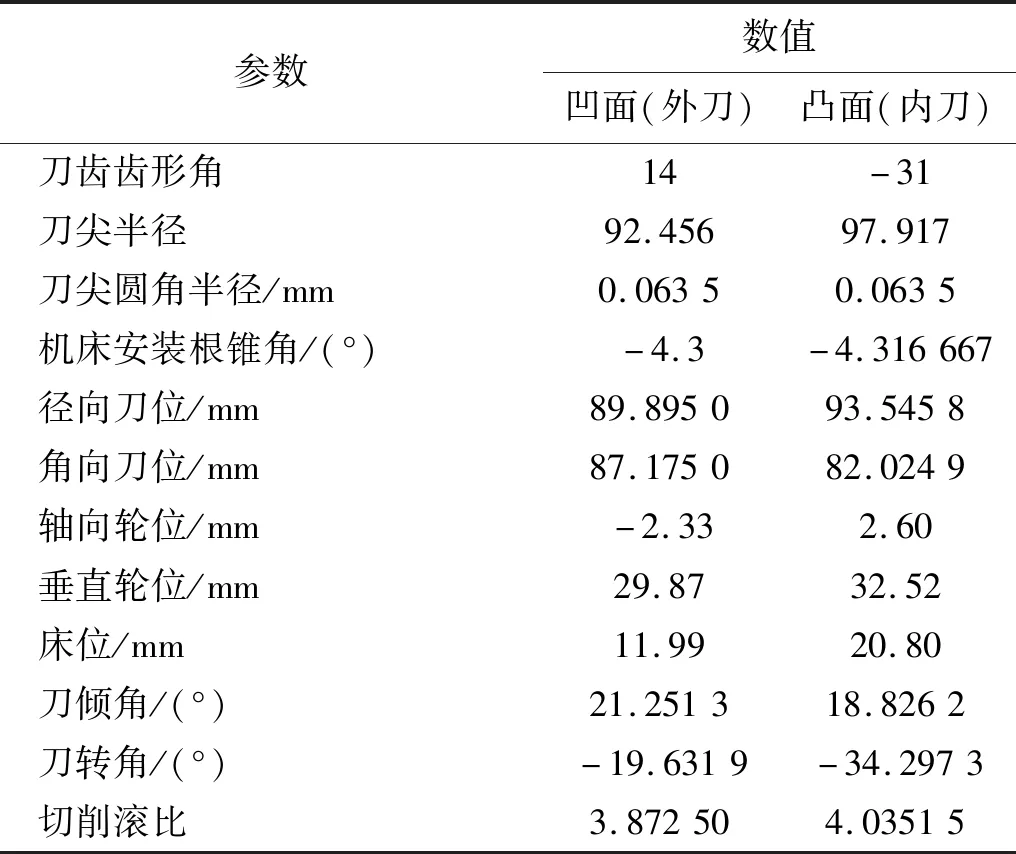
表3 小轮机床加工参数Tab.3 Machining parameters of the pinion

2.2 有限元模型构建

基于准双曲面齿轮副啮合及加工原理计算得到大、小轮齿面点云坐标，建立齿轮副三维模型。完成模型装配及单元设置，生成有限元模型节点和单元数据，综合考虑计算精度及效率的要求，选取小轮全齿、大轮18齿(总齿数41)模型进行分析。齿面接触力在接触区附近高度集中，强度随离接触区的距离增大而急剧减小，采用子结构法将齿面及齿根网格加密，其余部分稀疏化，如图3所示。

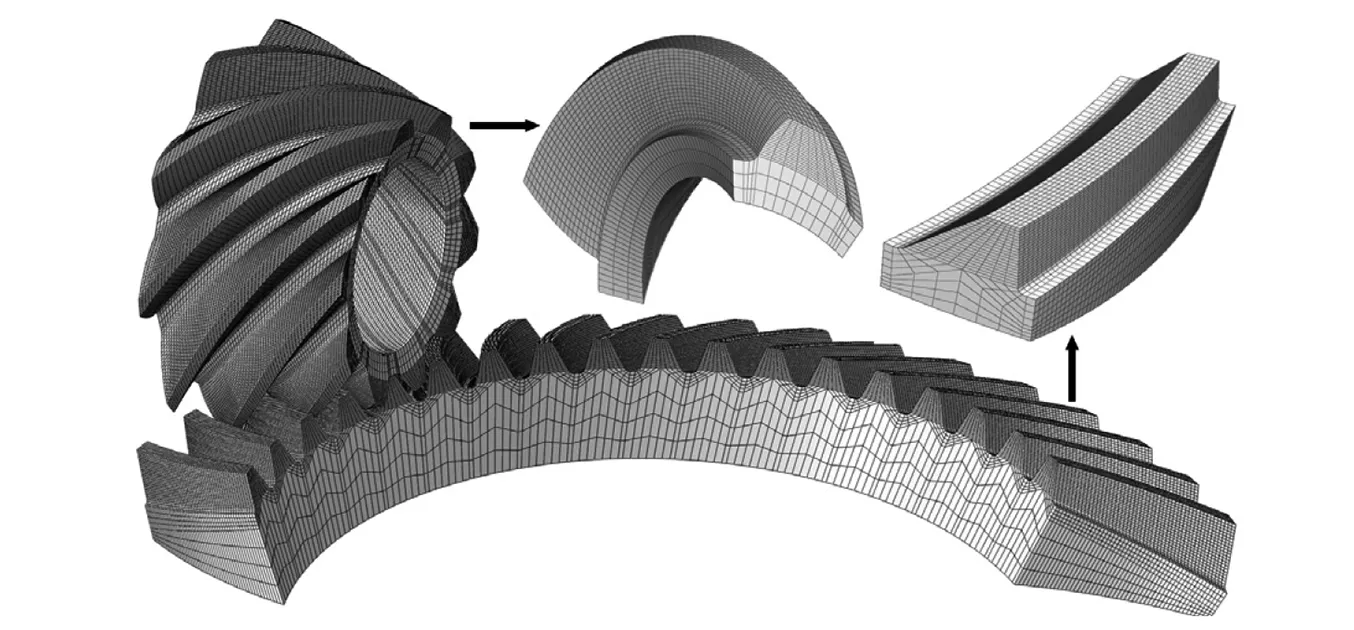
图3 准双曲面齿轮副有限元模型Fig.3 Finite element model of the hypoid gear drive

2.3 前、后处理设置

LTCA计算前处理包括分析类型设置、材料参数设置、单元属性定义、边界条件、载荷施加及输出变量等，部分参数设置见表4。

表4 部分前处理参数设置Tab.4 Preferences of the pretreatment

在大、小轮中心建立参考点，并与齿轮内孔节点刚性耦合，载荷及边界条件均施加在中心参考点处。为保证LTCA分析收敛，将整个啮合过程分3个载荷步进行设置：

(1)初始位置调整：旋转调整大、小轮的相对位置，使待接触齿面存在适量齿侧间隙；

(2)载荷步1：约束大轮中心参考点六向自由度，在小轮中心参考点以斜坡线性加载方式施加微小轴向转角，使齿面接触，消除齿侧间隙；

(3)载荷步2：约束小轮中心参考点六向自由度，释放大轮中心参考点的轴向转动自由度并以斜坡线性加载方式施加微小转矩，使齿轮达到理想的初始啮合状态。载荷步1、2使计算过程不存在刚体位移，保证初始接触迭代计算收敛；

(4)载荷步3：释放大、小轮各自轴向旋转自由度，约束其他自由度。在小轮中心参考点施加恒定轴向转速以驱动齿轮副，在大轮中心参考点施加恒定轴向负载扭矩，完成啮合过程。

3 LTCA算例分析

完成大轮4 000 N·m负载扭矩，小轮200 r/min驱动转速工况LTCA分析，计算各项啮合参数。

3.1 啮合印痕对比

通过与承载接触试验获得的齿面印痕进行对比，对LTCA计算结果进行验证。大轮齿面瞬时接触区的仿真结果与承载试验得到的印痕对比如图4所示，左侧子图从上至下为啮合过程中单齿面上瞬时接触区的移动过程，组成了右侧图中单个齿面上的完整印痕，可以看出LTCA与承载试验得到的齿面接触区均由大端齿顶移向小端齿根，吻合度较高，验证了LTCA分析的正确性。

图4 LTCA与承载啮合试验得到的齿面印痕对比Fig.4 Comparison of the contact patterns obtained by LTCA and loaded rolling test

3.2 等效啮合点

啮合过程中等效啮合点的位置如图5所示。准双曲面齿轮副啮合存在周期性，理想的等效啮合点轨迹为一闭环曲线。由于建模及仿真计算存在相对误差，本文得到的等效啮合点位于一个小的空间平面范围内。

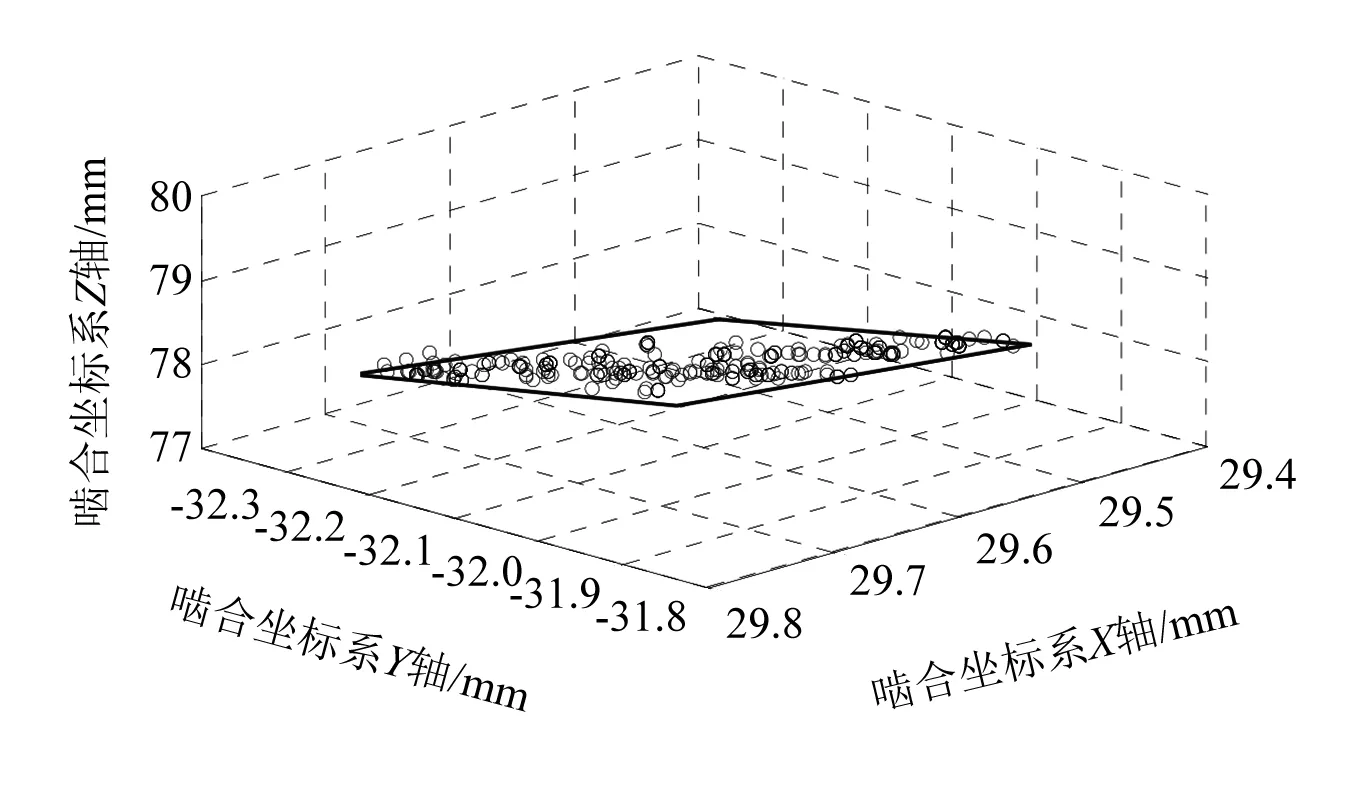
图5 4 000 N·m工况下等效啮合点位置Fig.5 Position of equivalent meshing points under 4 000 N·m

3.3 时变啮合参数

准双曲面齿轮副瞬时等效啮合力由接触齿面的法向接触力进行矢量相加而得到，求得该工况下等效啮合力如图6(a)所示。提取LTCA结果中大、小轮角位移，获得算齿轮副承载传动误差，如图6(b)所示。计算大、小轮接触节点理论位移与实际位移，得到齿轮副综合弹性变形，如图6(c)所示。根据得到的等效啮合力及综合弹性变形求得齿轮副时变啮合刚度，如图6(d)所示。

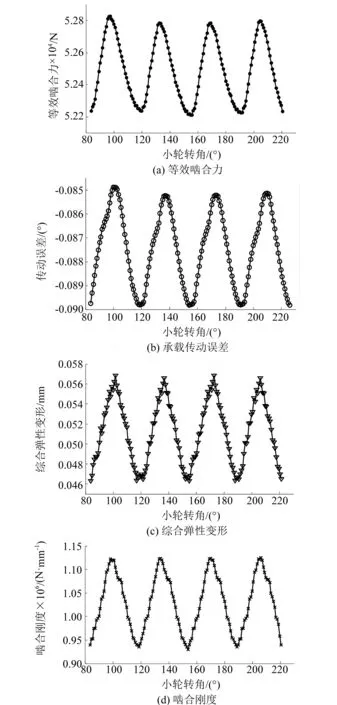
图6 4 000 N·m工况下的时变啮合参数Fig.6 Time-varying meshing parameters under 4 000 N·m

可以看出，齿轮副承载工况下的等效啮合力、承载传动误差、综合弹性变形、时变啮合刚度等参数均呈周期性变化，且无明显突变。小轮齿间间隔为36°，各项啮合参数波动频率与齿轮副啮合频率一致。

4 啮合参数演变分析

对齿轮副进行100～6 000 N·m不同载荷工况下的LTCA分析，计算各项时变啮合参数，分析其随载荷工况变化的演变规律。

4.1 齿面接触区

不同载荷下的单齿齿面接触区如图7所示。

图7 不同载荷下的齿面接触区Fig.7 Contact patterns on tooth surface under different loads

可以看出，齿面接触区随载荷增加逐渐由齿面中部扩展至全齿面，起始啮合位置逐渐移向大端，准双曲面齿轮大端处齿廓较厚，时变啮合刚度因此发生改变。

4.2 等效啮合力

不同载荷工况下的等效啮合力如图8所示，可以看出，随着载荷增大，等效啮合力的变化比例与负载扭矩的变化基本保持一致。不同载荷下，准双曲面齿轮副等效啮合力均呈周期性波动，且波动频率与齿轮副啮合频率一致。

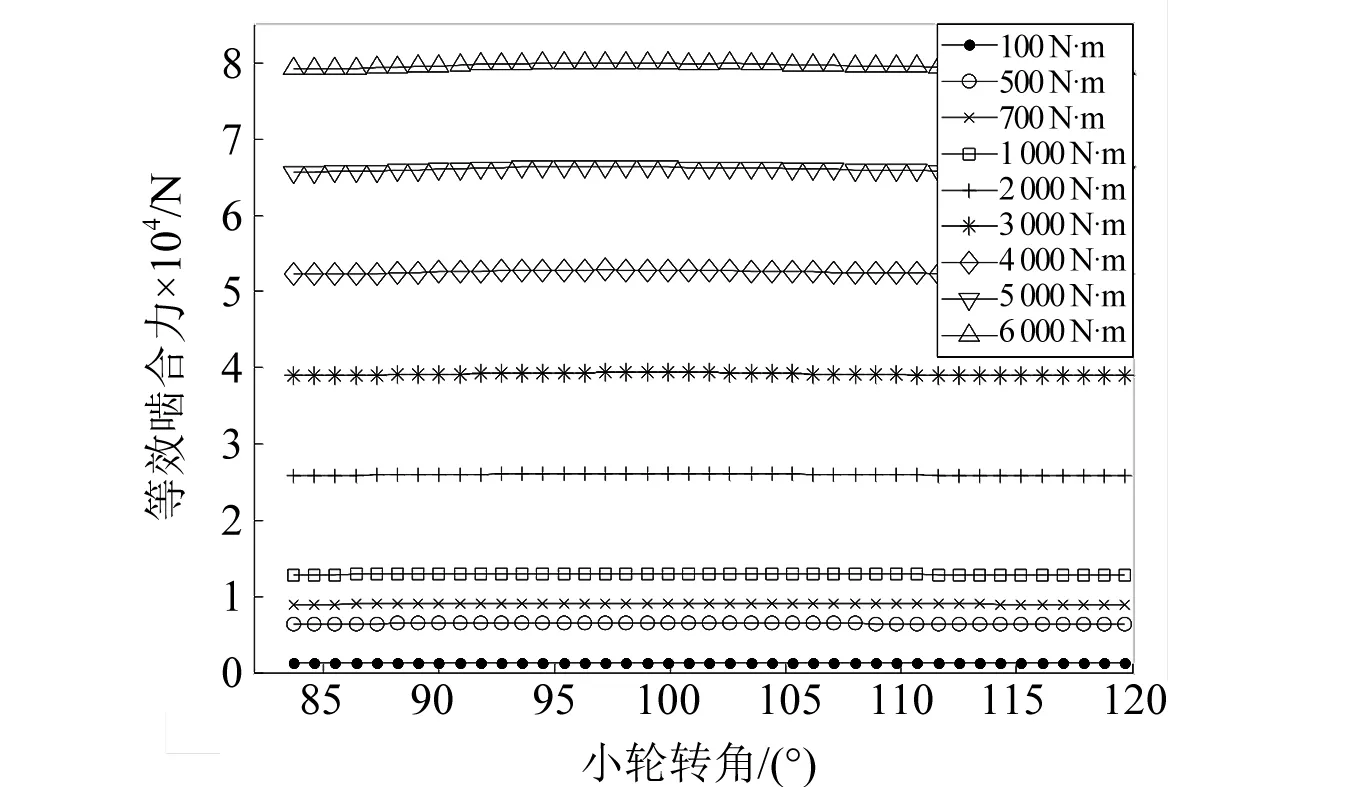
图8 不同载荷下的齿轮副等效啮合力Fig.8 Equivalent meshing force under different loads

4.3 承载传动误差

图9(a)为齿轮副不同载荷下的承载传动误差。可以看出，载荷较低时，随着负载扭矩的增加，齿轮副重合度增大，齿面接触区逐渐移至齿轮副设计时预设的理想接触区(算例齿轮副接触区由低载荷下的偏向大端逐渐移动至齿面中部，见图7)，到达理想接触区后传动误差的波动幅值最小。随着载荷继续增大，齿面接触区逐渐由齿面中部向大端和小端扩展(见图7)，根据准双曲面齿轮副的设计及加工原理，越靠近齿廓边缘，实际齿面相对于理论齿面的误差越大，大、小轮啮合时的误差因此上升，故齿轮副传动误差的波动幅值转而增大，总体呈现出“先减小后增大”的演变趋势。

图9 不同载荷下的啮合参数Fig.9 Meshing parameters under different loads

4.4 齿面接触力及实际重合度

图9(b)为不同载荷下单齿对齿面接触力，图中曲线从左至右依次为第4、第5、第6对齿的齿面接触力，从下至上依次为100，300，500，700和1 000～6 000 N·m工况下计算结果。准双曲面齿轮副单齿接触力随载荷增加而所上升。图9(c)为不同载荷下的准双曲面齿轮副实际重合度大小，载荷较低时，实际重合度随载荷增加的升高幅度较为明显，随载荷增大实际重合度的变化趋于平缓。

4.5 综合弹性变形及时变啮合刚度

不同载荷下的综合弹性变形如图10(a)所示，可以看出，准双曲面齿轮副综合弹性变形量及其波动幅值随载荷增加均逐渐增大。

根据获得的不同载荷下的时变等效啮合力和综合弹性变形计算算例齿轮副不同载荷下的承载啮合刚度，如图10(b)所示。

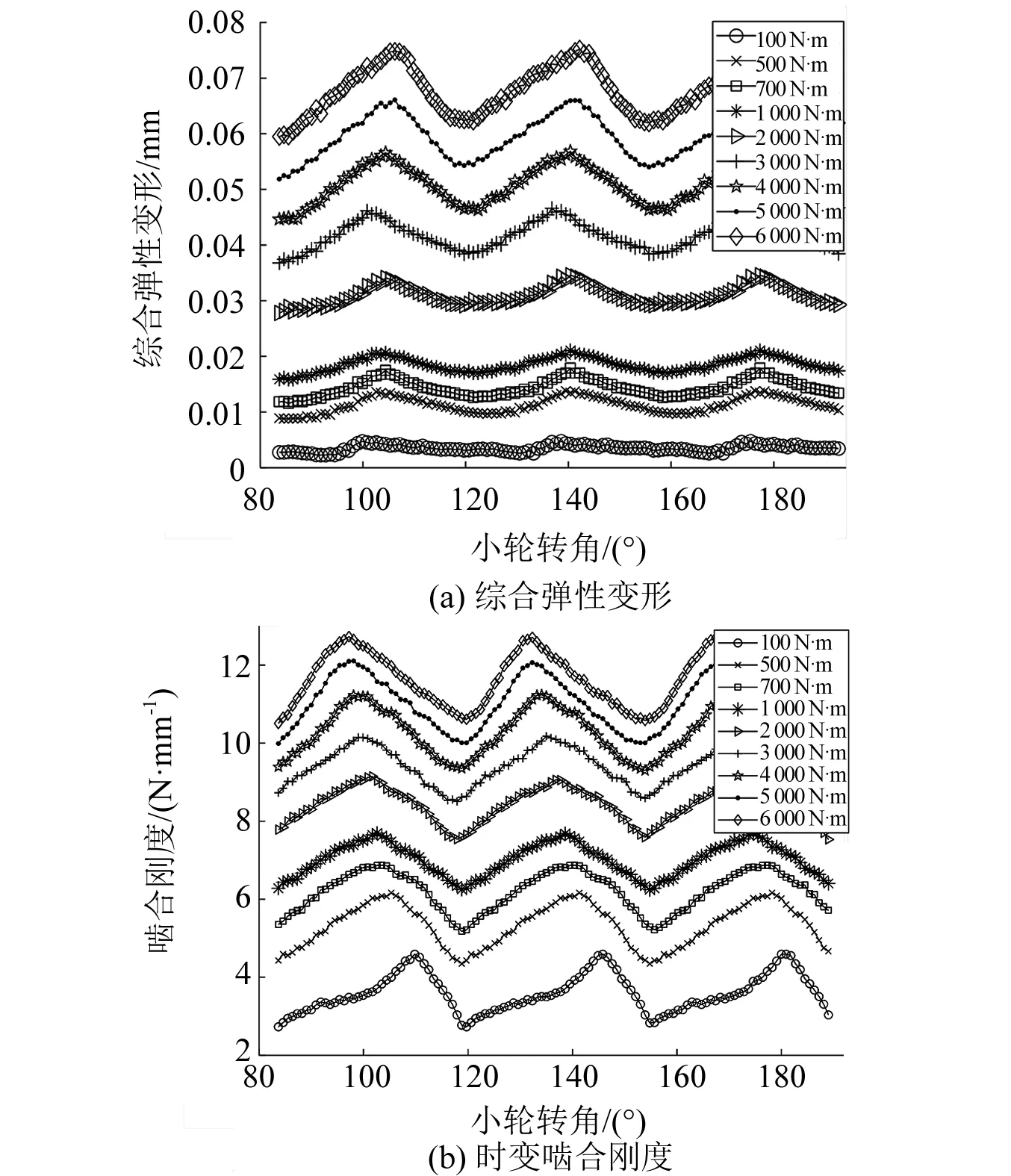
图10 不同载荷下综合弹性变形及时变啮合刚度Fig.10 Comprehensive elastic deformation and time-varying meshing stiffness under different loads

可以看出，承载工况下时变啮合刚度曲线呈周期性波动，波动频率与齿轮副啮合频率一致。不同载荷下周期变化的刚度曲线的形状差别显著，低载荷时单周期内的曲线峰值靠近末端，随载荷增加峰值逐渐前移，以峰值为中点左右非对称。原因是载荷增加使齿面接触区逐渐移向大端，啮合点处齿厚增大，齿廓不易发生弯曲、剪切变形。载荷越大越早出现大端接触，即越早出现刚度峰值，本文计算结果与工程实际相符。

5 结 论

针对以往研究中近似、等效计算准双曲面齿轮副啮合变形量的不足，本文对准双曲面齿轮副进行了不同载荷下的承载接触分析，并提取、计算了轮齿真实变形量及承载传动误差、时变啮合刚度、实际重合度等参数，得出以下结论：

(1)准双曲面齿轮副不同载荷下的等效啮合力、承载传动误差、综合弹性变形及时变啮合刚度等参数均呈周期性波动，无显著突变，波动频率与齿轮副啮合频率一致。齿面啮合印痕随载荷增加逐渐由齿面中部扩展至全齿面，起始啮合位置随载荷增加逐渐移向大端。

(2)准双曲面齿轮副实际重合度随载荷增加呈非线性趋势上升。低载荷时，实际重合度随载荷增大迅速增加，载荷达到一定大小后，重合度的变化趋于平缓。低载荷下，同时啮合的齿对数受载荷变化影响显著，齿间载荷分配及轮齿动载荷变化在动力学分析中应得到重视。

(3)准双曲面齿轮副啮合变形及其波动幅值随载荷增加逐渐增大。随载荷上升，啮合刚度曲线单周期内峰值逐渐前移，以峰值为中点左右非对称。传动误差波动幅值随载荷增加呈先增大后减小的演变趋势，存在传动误差波动幅值较小的载荷区间。载荷变化时啮合刚度及传动误差均具有较强非线性，在准双曲面齿轮系统动力学分析时准确描述啮合刚度和传动误差是很有必要的。